Development and Simulation of a Tensile Test Apparatus Down to Liquid Hydrogen Temperature Region
-
摘要:
为了满足当前液氢工程领域对材料力学性能测试的需求，以两台G-M制冷机为冷源、氦气为载冷介质，设计和研制了一台低温材料拉伸测试装置。该装置可实现14~300 K温区内各类固体材料的拉伸试验。采用液氮预冷的方式，样品降温至14 K用时仅7 h。对试验腔内试件的温度分布进行仿真模拟，结果表明试件的温度梯度主要存在于纵向，而横向没有明显的温差。对316 L不锈钢试样进行多工况拉伸性能测试，可重复性高于97.8%。所得304和316 L不锈钢材料的屈服强度和抗拉强度测试数据与文献数据相比最大相对偏差仅为6.3%，该深冷温区拉伸测试装置具有较高的可靠性和准确性。
Abstract:To meet the requirement of material mechanical properties testing in the field of liquid hydrogen engineering, with two G-M refrigerators as cooling source and gas helium as cooling medium, a tensile test apparatus at cryogenic tempe-rature was designed and developed. It can be applied in the temperature range of 14 K to 300 K and takes only 7 hours to reach the lowest temperature of 14 K by pre-cooling with liquid nitrogen. The temperature distribution of the specimen in the test chamber was simulated. The results showed the temperature gradient of the specimen mainly existed in the longitudinal direction, while there was no temperature difference in the transverse direction. The tensile properties of SS316L and SS304 were measured and compared with literature data. The repeatability of the present data was found to be higher than 97.8%. The maximum relative deviation between the measuring data of yield strength and tensile strength and the literature data was only 6.3%, showing that the test results of the tensile test device have high credibility and accuracy.
-
0. 引 言
随着航空航天、清洁能源、低温超导、远红外探测等技术的发展，各种材料特别是一些新材料和复合材料在深冷环境下的应用愈加广泛，它们在低温下的力学性能是最被关心的内容之一。与常温环境不同，低温下材料的力学性能会发生显著变化，如低温工程中广泛使用的2219-T851铝合金和316 L不锈钢在深低温区会表现出更大的拉伸强度[1-2]。因此，开展低温环境下材料强度、塑性和韧性等力学性能的研究是满足工程应用必不可少的一环。部分材料低温下拉伸性能数据（屈服强度、抗拉强度等）可以从手册中查取，但该方法面临着覆盖温区窄（尤其是77 K以下温区）、数据陈旧、可靠性低和材料种类少等问题，无法满足新的工程实际要求。开发新的宽范围低温拉伸力学性能测试装置对于获取77 K以下温区新材料的实测力学性能数据具有重要意义。目前，材料低温拉伸测试装置大多采用低温液体浸泡试样或低温气体吹扫试样的方式实现试件冷却[3]，常用的低温液体有液氮和液氦。但这类方式需要消耗大量低温流体，Desisto等[4]利用液氦冷却试样，测试室体积仅为1.2 L，但要冷却试样至4.2 K至少需要消耗5 L液氦。Belton等[5]研制的液氢温区力学性能测试装置，单次测试需要消耗140 L的液氢。在液氮温度以下，测试所使用的液氦属于稀缺能源，价格昂贵，而液氢不仅来源受限且极其危险，不便于实际测试操作。此外，这种方式通常只适合测试特定温度点（如4.2 K、20 K或77 K）的力学性能，无法满足研究宽温区材料力学性能随温度变化规律的要求。为解决液氦/液氢介质试验成本高、来源受限、安全性差等问题，一些学者[6-7]引入了新的冷源类型。其中G-M制冷机作为商业化产品技术逐步成熟，成为理想的替代冷源。但相关的低温力学性能测试装置降至目标低温用时均超过10 h，也未见对腔内样品的温度分布情况的实测或仿真研究报道，无法判断样品各位置温度是否均已降至目标温度。表1对国内外具有代表性的低温力学性能测试装置及其特点进行了归纳总结。
表 1 代表性低温力学性能测试装置Table 1. Representative mechanical property test device at low temperature冷源 测试温度/K 单次测试消耗/降温时间 测试样品 参考文献 液氦 4.2 5 L液氦、3 L液氮 302不锈钢等 DeSisto等[4] 液氢 20 140 L液氢 6061-T6铝合金 Belton等[5] 液氦 4.2 \ 聚苯乙烯 Foley等[8] 液氦 4.2 10~12 L 2024-T8铝合金 Kaufman等[9] 液氦、液氮、酒精干冰 4.2、77、195 \ 25Mn5Cr1Ni钢 陈国邦[10] 液氢、气氦 20 \ 304 L等 Deimel等[11] G-M制冷机 4.2~300 20 h以上 S30408钢 姜恒等[6] G-M制冷机 8~300 14 h 5A06铝合金 谢世永等[7] 本文介绍了一套温度稳定可控的低温材料拉伸测试装置，采用两台G-M制冷机为冷源，以氦气为导冷介质，测试温度范围为14~300 K，将液氮预冷管路耦合进低温制冷机制冷系统，降温时间仅为7 h。本文利用COMSOL仿真软件对测试腔及试件温度进行仿真研究，以典型材料为样品，验证了不同温度下所测拉伸强度与文献数据的吻合度。
1. 低温拉伸测试装置设计与搭建
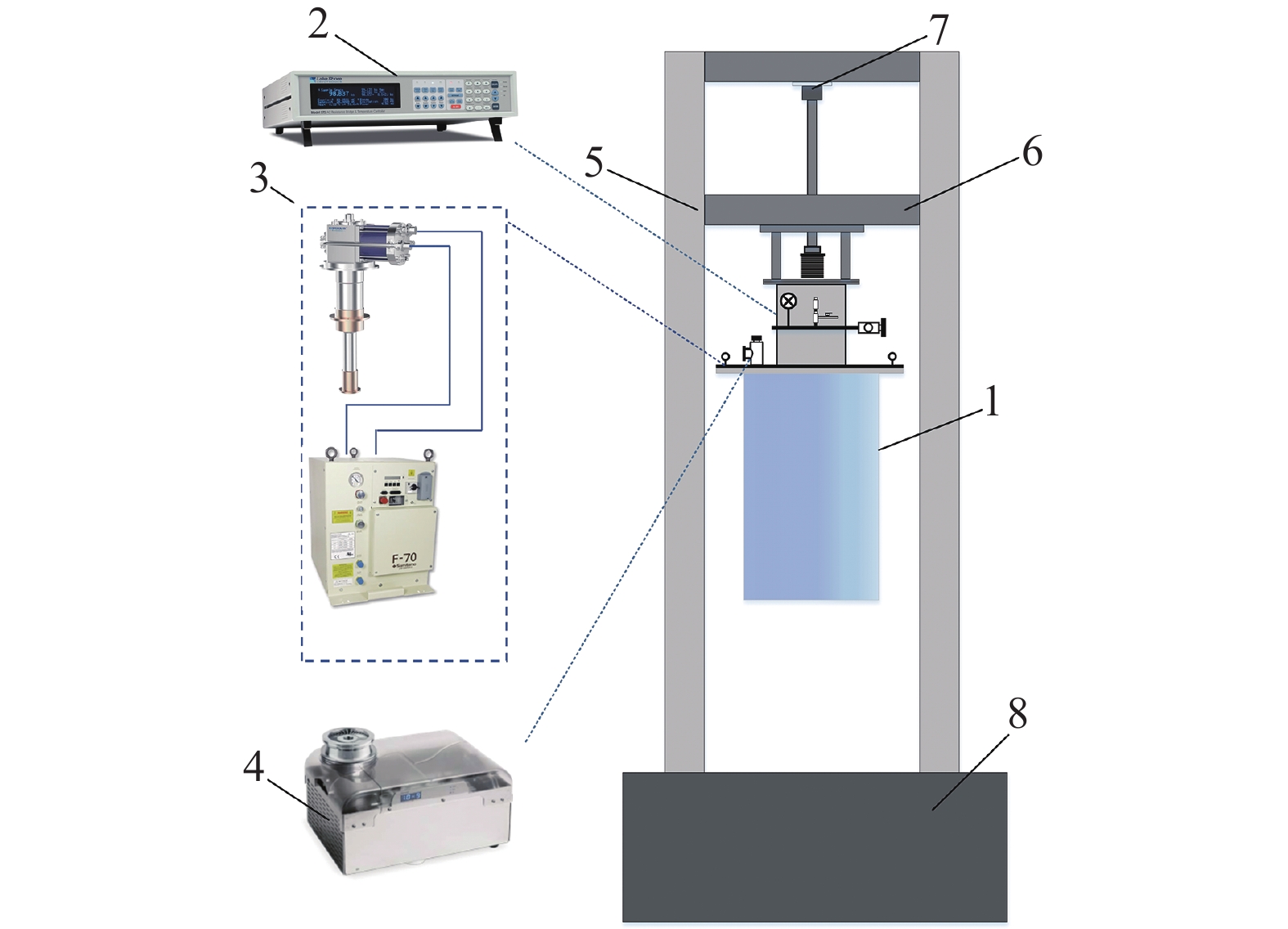
低温拉伸测试装置是在通用电子万能试验机基础上增加低温冷却和绝热温控系统而成，重点解决万能试验机拉伸杆的高低温穿仓和样品低温夹具问题。低温冷却和绝热温控系统包括真空腔、温控系统、冷却系统和真空抽气系统。低温拉伸测试装置系统组成如图1所示。
![]()
图 1 低温拉伸测试装置系统组成图1. 真空腔；2. 控温系统；3. 冷却系统；4. 真空抽气系统；5. 万能试验机龙门架；6. 移动横梁；7. 力传感器；8. 万能试验机底座。Figure 1. Composition of low temperature tensile test system1.1 真空腔
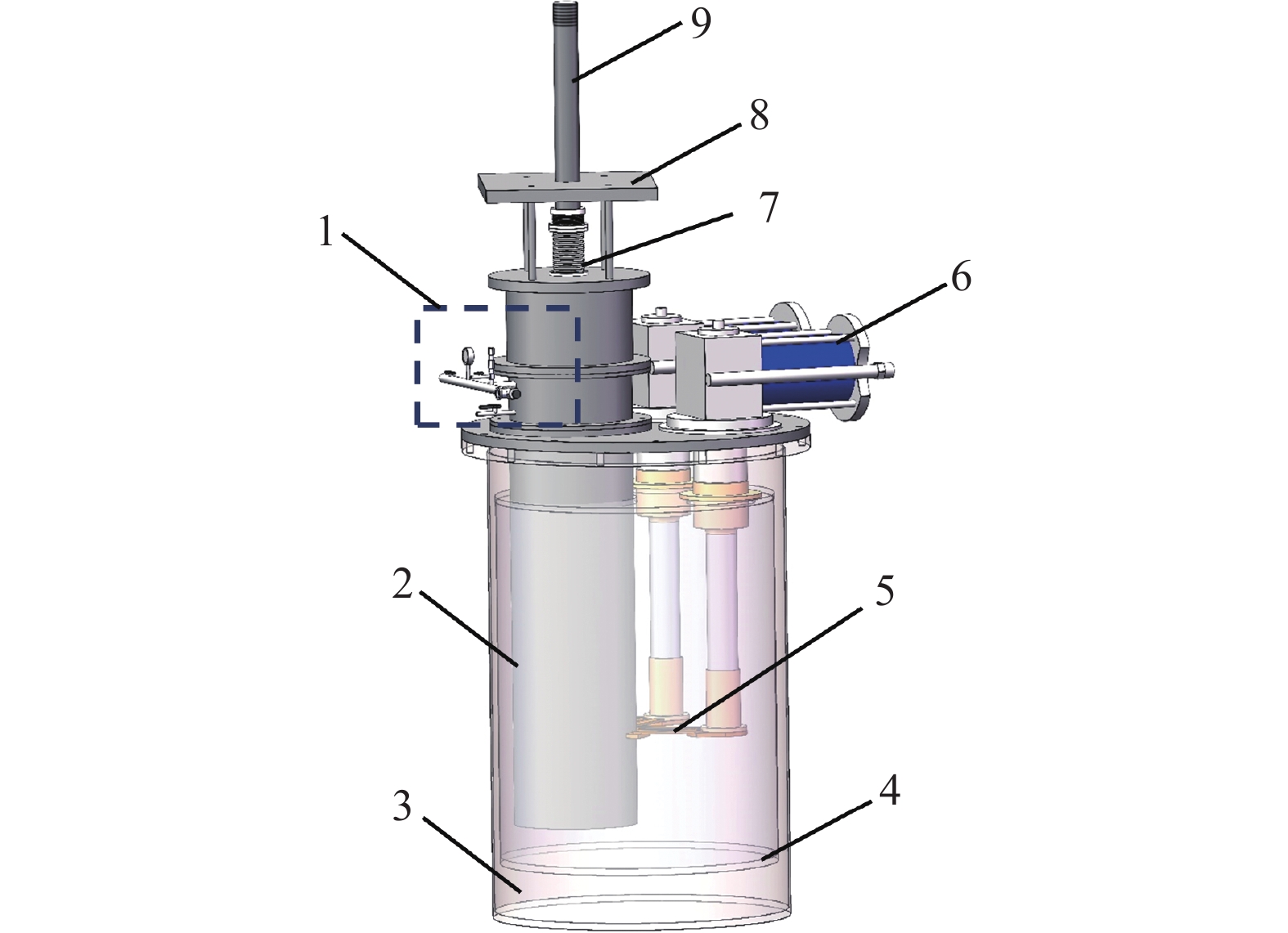
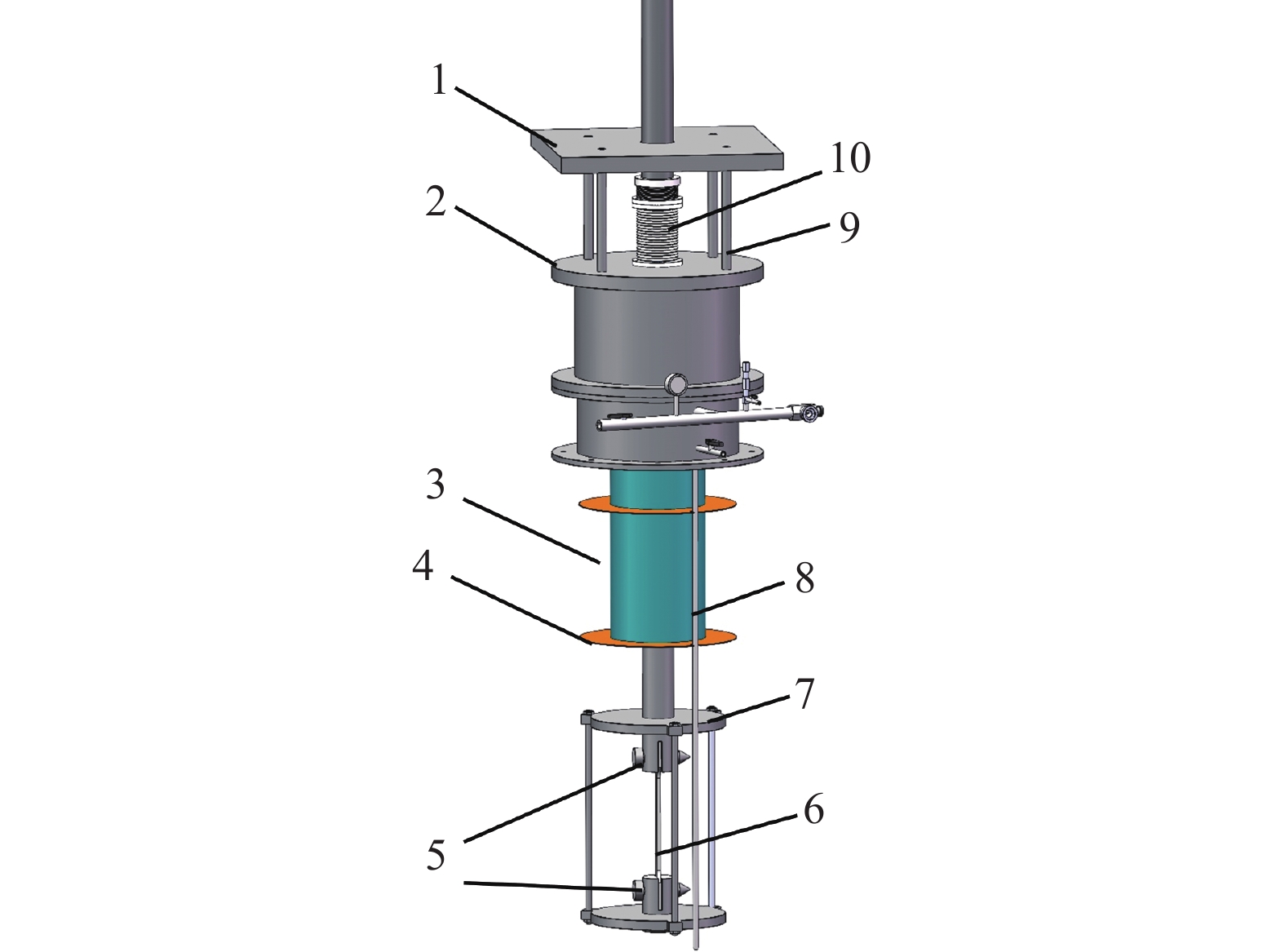
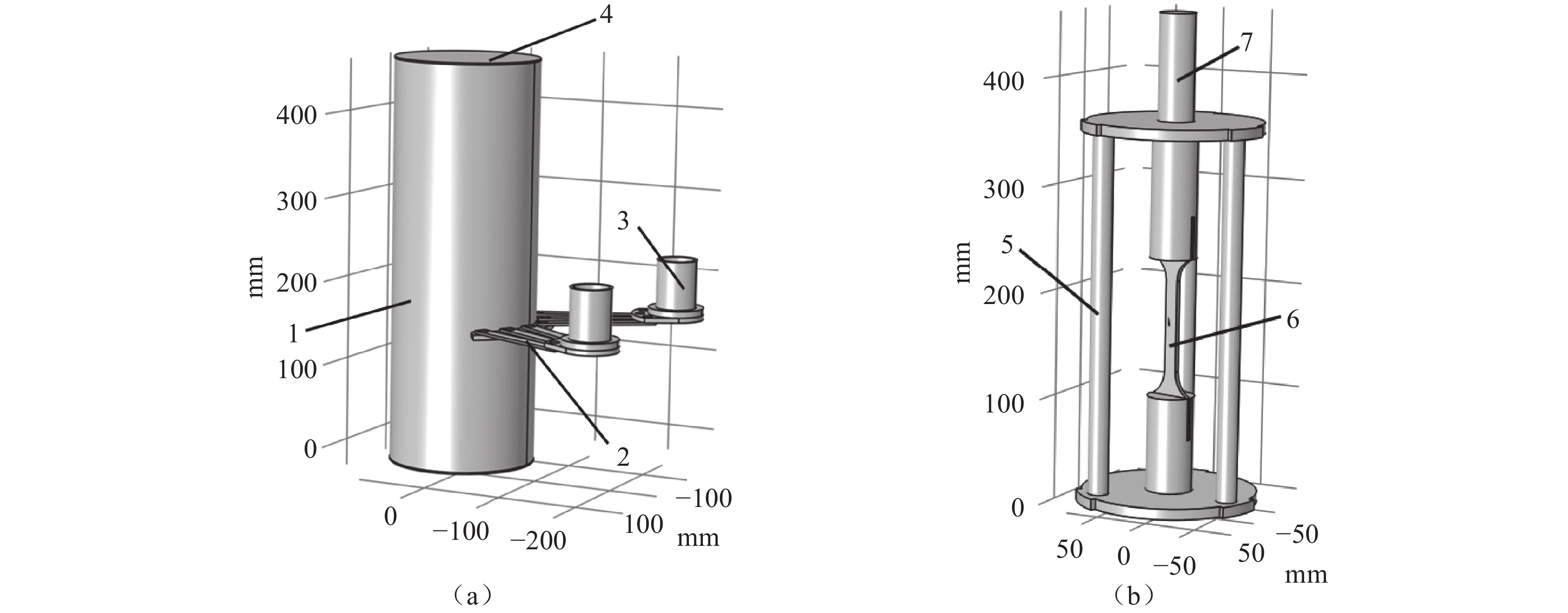
真空腔包括低温试验腔及其组件、热辐射防护冷屏、真空室及其他零部件，其三维结构如图2所示。工作时低温试验腔内充满氦气，其内部结构如图3所示。
![]()
图 2 真空腔三维结构图1. 阀门操作区；2. 低温试验腔；3. 真空室；4. 冷屏；5. 导热热桥；6. G-M制冷机；7. 波纹管；8. 连接板；9. 通用力学试验机拉伸杆。Figure 2. 3D Construction of cryogenic chamber![]()
图 3 试验腔内部结构图1. 连接板；2. 腔顶法兰；3. 隔热泡沫；4. 铜屏；5. 样品夹具；6. 样品；7. 拉伸试验工装；8. 液氮输送管路；9. 试验腔连接杆；10. 波纹管。Figure 3. Internal Construction of test chamberG-M制冷机二级冷头与试验腔外壁间使用紫铜热桥连接。腔体外采用真空绝热方式；为充分利用制冷机一级冷头的冷量，在试验腔与真空腔内壁间插入冷屏，使之与制冷机一级冷头连接。力学试验机拉伸杆穿过移动横梁、连接板及腔顶法兰，为解决力学试验机拉伸杆高低温穿仓问题，在拉伸试验工装上部，力学试验机拉伸杆在竖直方向上依次布置铜屏和隔热泡沫，用以减少辐射漏热和气体导热。上下试件夹具均为304不锈钢材质，采用螺纹连接方式与力学试验机拉伸杆底端和拉伸试验工装底部相连。试验腔顶部的连接板与万能试验机移动横梁通过螺栓固定连接，进行低温力学性能测试时，移动横梁带动真空腔向下移动，拉伸杆顶端则与万能试验机顶部的力传感器连接固定。连接板和腔顶法兰间设有波纹管及滑动密封件，既便于横梁沿着拉伸杆移动，又能密封试验腔内气体。真空腔移动时试件底端随之移动，由于拉伸杆底端与上夹具连接，故试件顶端固定不动，因此横梁向下移动时对试件产生了向下的拉力，通过试验机顶部的力传感器测得。
1.2 温控系统
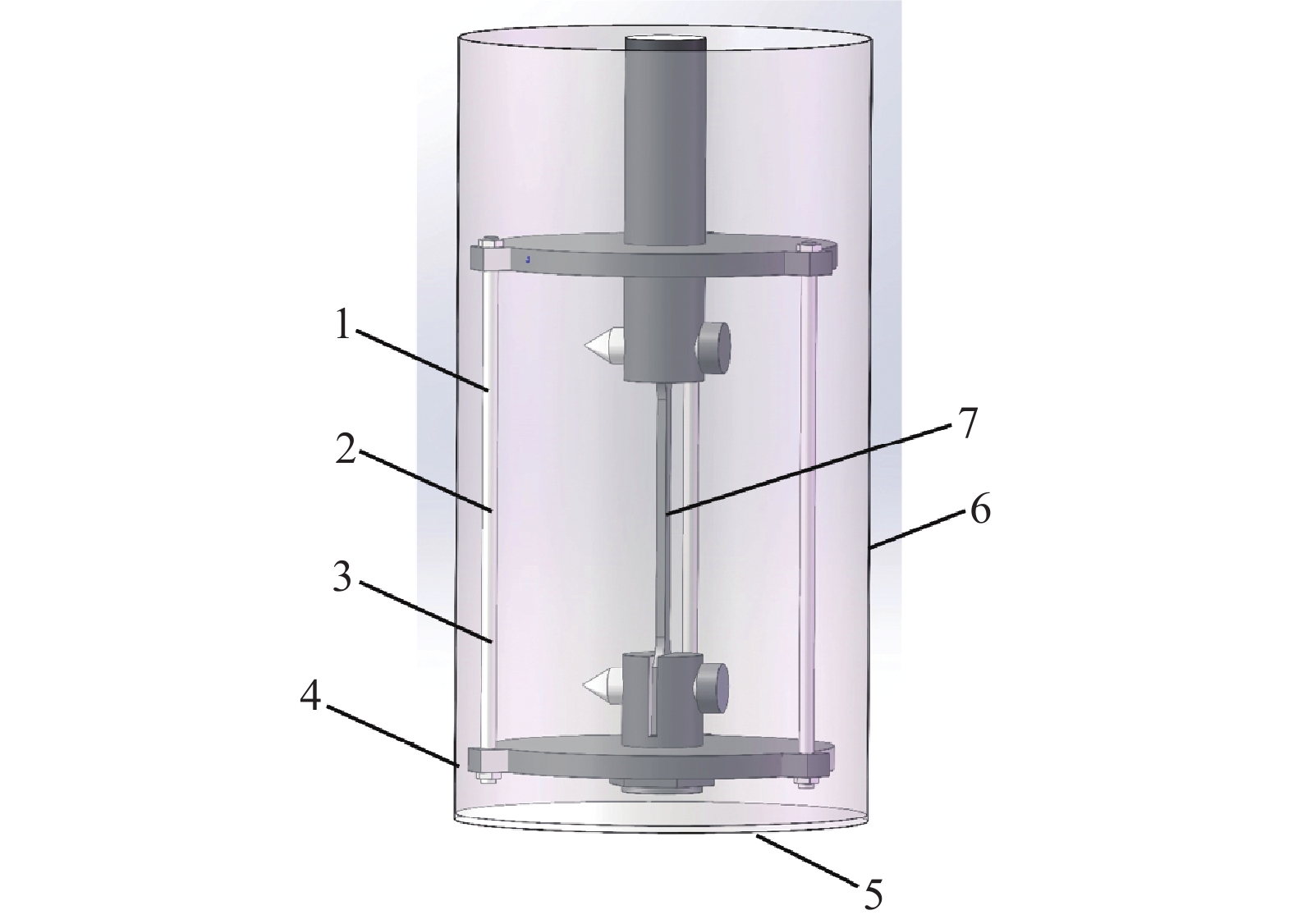
温控系统负责整个系统的温度采集、控制、输出等功能，该系统中包含多支温度计、加热电阻和控温仪。制冷机二级冷头、低温试验腔底部和外壁均布置碳电阻温度计，腔体外壁另布置加热电阻用来调节腔室内氦气温度。在支撑架的上、中、下3个位置分别布置3支PT1000温度计用以估测试件温度，如图4所示。3支温度计读取支撑架在竖直方向上不同位置处的温度数据，这样有利于估测试件表面温度的均匀性和稳定性。基于收集的温度信号配合PID方法调节电加热功率自动实现目标温度调控。
![]()
图 4 温度计布置示意图1、2、3. PT1000温度计；4、5. 碳电阻温度计；6. 加热电阻；7. 试件。Figure 4. Location of temperature sensors1.3 冷却系统
冷却系统中G-M制冷机的二级冷头直接冷却低温试验腔壁面，进而冷却腔体内氦气，被冷却的氦气再对被测试件、支架和夹具等部件降温。为了使拉伸试样最低温度降至14 K，经核算低温试验腔的热负荷，如表2所列，确定使用两台二级G-M制冷机。由于试验腔体积较大、腔体内部件繁杂，且充满常温氦气后热容很大，若仅依靠制冷机冷头，将试件从室温降至14 K需要很长时间，单次试验时间成本较高。
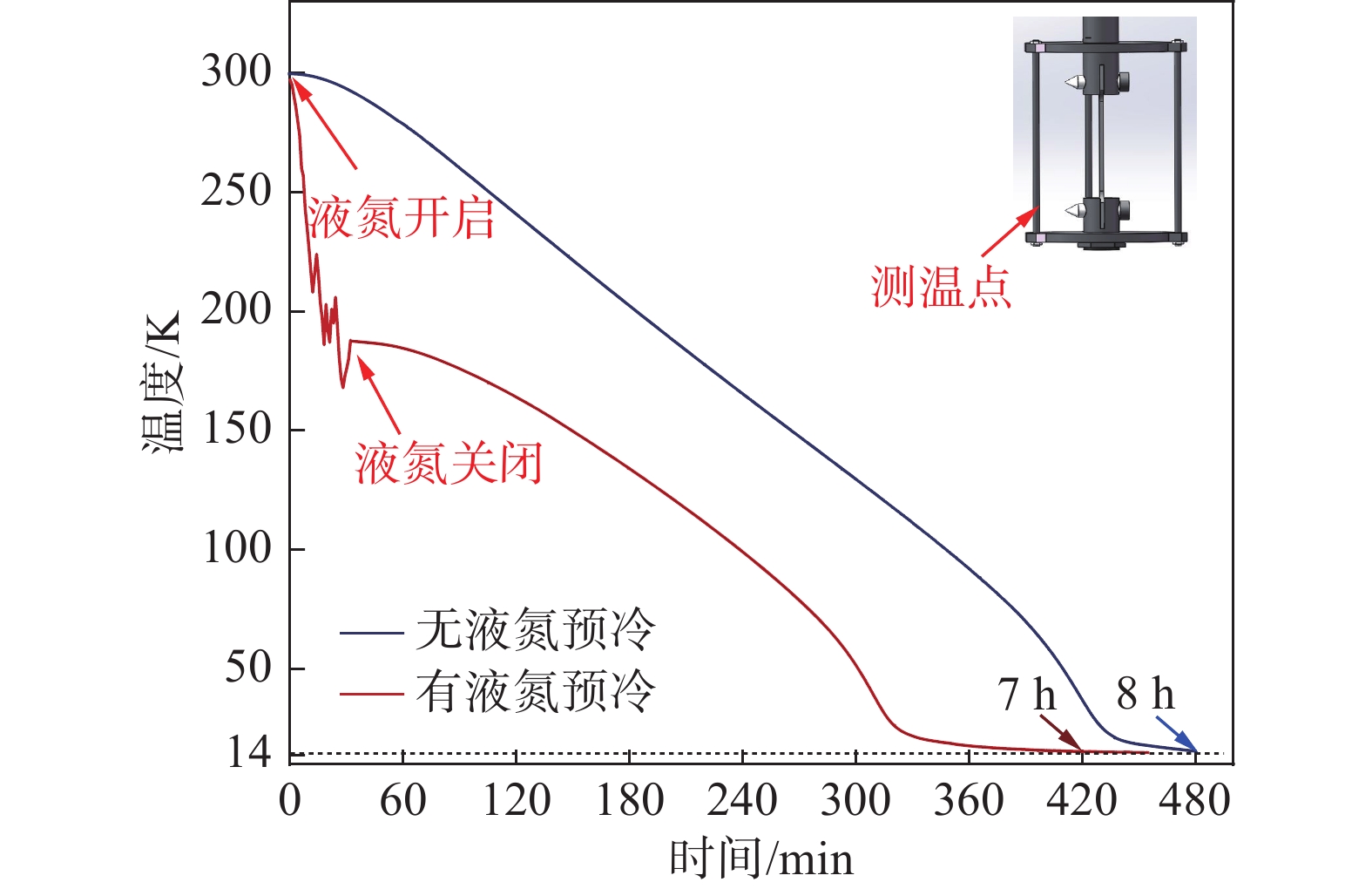
表 2 最低温度时试验腔漏热分析Table 2. Heat load of test chamber at lowest temperature漏热形式 漏热量/W 拉伸杆漏热 3.73 不锈钢壁漏热 4.02 液氮管路漏热 0.15 导线漏热 0.37 剩余气体导热 0.15 筒体辐射漏热 15.7 总计 24.12 鉴于许多低温力学性能测试装置中都使用液氮作为冷屏冷却介质或者辅助冷源，如Kaufman等[9]采用双杜瓦结构的低温恒温器冷却试件，其外部杜瓦使用液氮作为冷屏冷却介质。本系统采用一根管路将液氮通入低温试验腔底部，使液氮与腔体内试件、支撑架及其他部件换热气化后排出腔体，对低温试验腔进行预冷。预冷结束后使用氦气吹除腔体内残余的氮气，避免当降温至77 K以下时冻堵以及起阻碍降温的副作用。分别在采用液氮预冷和不采用液氮预冷的情况下，利用G-M制冷机制冷，对该系统进行降温测试。两次实际降温测试曲线如图5所示，不采用液氮预冷时降至最低温度14 K需要8 h；当采用液氮预冷则可以在7 h内将试样腔温度从300 K降至14 K，降温时间缩短了近13%。
![]()
图 5 实际降温测试的温度-时间变化曲线Figure 5. The variation curves of temperature with in actual cooling test1.4 温度、力和位移测量系统
试样腔内的温度、试件形变量以及受力分别采用Lakeshore 336温控仪、CLH-special引伸计和Transcell® DBSL-30t力传感器进行测量。温控仪具有8路测温通道和2路独立控温输出，测温精度为0.001K。CLH-special是一支定制的大变形引伸计，标距为50 mm，测量范围为±25 mm，分辨率为1 μm。力传感器DBSL-30t最大量程为30吨，示值相对误差为0.5%。利用LabView® 软件编写温度采集和电加热功率控制程序。采用三思UTM5305X型电子万能试验机和配套的专业数据采集程序完成力和形变量的数据采集。
1.5 测试系统的测量误差分析
试件应力与应变的计算公式分别为式（1）（2）。试件应力及应变测量的相对误差可以分别通过式（3）（4）计算。
$$ {\sigma _{(T)}} = \frac{{{F_T}}}{{{W_{293}} \times {D_{293}}}} $$ (1) $$ {\varepsilon _{(T)}} = \frac{{d{L_T}}}{{{L_{293}}}} $$ (2) $$ \frac{{\vartriangle \sigma }}{\sigma } = \pm \sqrt {{{\left( {\frac{{\delta {F_T}}}{{{F_T}}}} \right)}^2} + {{\left( {\frac{{\delta {W_{293}}}}{{{W_{293}}}}} \right)}^2} + {{\left( {\frac{{\delta {D_{293}}}}{{{D_{293}}}}} \right)}^2} + {{\left( {\frac{{\delta T}}{T}} \right)}^2}} $$ (3) $$ \frac{{\vartriangle \varepsilon }}{\varepsilon } = \pm \sqrt {{{\left( {\frac{{\delta \left( {d{L_T}} \right)}}{{d{L_T}}}} \right)}^2} + {{\left( {\frac{{\delta {L_{293}}}}{{{L_{293}}}}} \right)}^2} + {{\left( {\frac{{\delta T}}{T}} \right)}^2}} $$ (4) 式中：$ {\sigma _{(T)}} $为试件应力，MPa；$ {\varepsilon _{(T)}} $为材料应变，%，$ {F_T} $为任意温度下试件所受拉力，N；$ {L_T} $为任意温度下试件标距段长度，mm；$ {W_{293}} $、$ {D_{293}} $和$ {L_{293}} $分别为国际上普遍采用的温度为293 K时试件的宽度、厚度和标距，mm。$ \dfrac{{\delta {F_T}}}{{{F_T}}} $表示力传感器的测量误差，$ \dfrac{{\delta {W_{293}}}}{{{W_{293}}}} $表示试件宽度测量的误差，$ \dfrac{{\delta {D_{293}}}}{{{D_{293}}}} $表示试件厚度测量的误差，$ \dfrac{{\delta \left( {d{L_T}} \right)}}{{d{L_T}}} $表示引伸计的测量误差，$ \dfrac{{\delta {L_{293}}}}{{{L_{293}}}} $表示试件标距的测量误差，$ \dfrac{{\delta T}}{T} $表示温度测量引入的误差。
表3为误差计算数据。由表3可知，本装置强度和伸长率测量的相对误差分别为±0.92%和±0.67%。
表 3 误差计算数据Table 3. Error calculation data误差项 误差值/% $ \dfrac{{\delta {F_T}}}{{{F_T}}} $ ±0.5 $ \dfrac{{\delta {W_{293}}}}{{{W_{293}}}} $ ±0.08 $ \dfrac{{\delta {D_{293}}}}{{{D_{293}}}} $ ±0.25 $ \dfrac{{\delta \left( {d{L_T}} \right)}}{{d{L_T}}} $ ±0.006 $ \dfrac{{\delta {L_{293}}}}{{{L_{293}}}} $ ±0.02 $ \dfrac{{\delta T}}{T} $ ±0.67 $\dfrac{ {\Delta \sigma } }{\sigma }$ ±0.92 $\dfrac{ {\Delta \varepsilon } }{\varepsilon }$ ±0.67 2. 仿真分析
由于材料力学性能对温度的变化较敏感，需要对本研究中低温试验腔内试件的温度分布均匀性进行分析，重点关注试件测试段在纵向与横向的温度分布，这对于确保低温拉伸测试结果的准确性具有重要意义。此外，由于测试腔顶部漏热的存在，试件尺寸的设计（特别是平行段长度）尤为重要。当试件尺寸过大时，试件顶部受漏热影响严重，导致试件出现“上热下冷”的情况，这种温度不均匀现象将对测试结果产生影响。文献中对此研究较少，本研究通过仿真分析确定该测试装置所适用试件的平行段最大尺寸，以确保低温拉伸测试结果的准确性。
2.1 模型建立
由于难以直接使用温度传感器测试试件内部温度，利用仿真软件的固体和流体传热模块对试样腔内及试件的温度进行有限元仿真。模型中试件厚度为4 mm，平行段长度为80 mm，总长度为205 mm。由于试验腔内壁直径与试验腔内铜屏外径仅相差1 mm左右，流经铜屏的氦气量极小，因此假定以腔体纵向的第一片铜屏作为模型顶部封闭面，建立的仿真模型如图6所示。该模型与试验器件吻合，部分细节如温度传感器、加热电阻、引伸计及引线等忽略。
![]()
图 6 有限元模型1. 低温试验腔；2. 导热热桥；3. 制冷机二级冷头；4. 铜屏；5. 支撑杆；6. 试件；7. 万能试验机拉伸杆。Figure 6. Finite element simulation model2.2 网格划分及条件设置
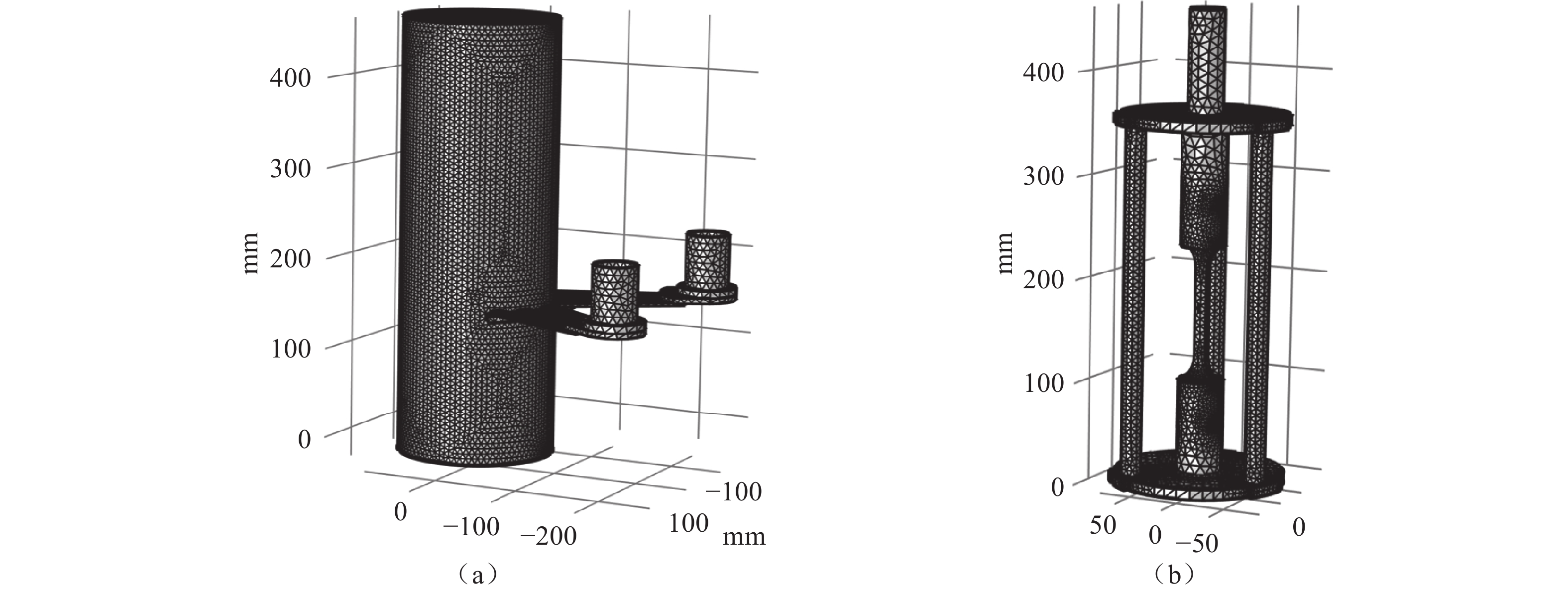
模型的网格划分采用物理场控制的自由四面体结构，并对腔壁、试件和各接触处进行了细化处理，如图7所示。经网格无关性验证后，构建的完整网格包含13282个边单元、212688个边界元和1417089个域单元。
该模型中的支撑杆选用仿真软件材料库中的304不锈钢，试验腔、冷头及导热热桥为紫铜材料，腔内气体为氦气，腔内氦气流动设置为可压缩流动并包含重力。由于材料的热导率与温度相关，因此采用美国NIST材料物性库中给出的式（5）[12]进行计算；紫铜材料的各项系数如表4所列。
表 4 紫铜热导率计算公式系数Table 4. Copper thermal conductivity calucation formula coefficient系数 取值 系数 取值 系数 取值 a 1.8743 d 0.13294 g −0.0051276 b −0.41538 e 0.26426 h 0.0014871 c −0.6018 f −0.0219 i 0.003723 $${\log _{10}}{k_{\rm{b}}} = \frac{{(a + c{T^{0.5}} + eT + g{T^{1.5}} + i{T^2})}}{{(1 + b{T^{0.5}} + dT + f{T^{1.5}} + h{T^2})}}$$ (5) 式中：$ {k_{\text{b}}} $为材料的热导率；T为温度；
氦气的密度、热导率和动力黏度与温度之间的变化关系根据Refprop软件中给出的数据[13-14]拟合得式（6）（7）（8）。制冷机二级冷头制冷功率与温度的关系由厂家提供的数据拟合得式（9）。
$$ {\rho _{{\text{helium}}}} = 7.853\;38{e^{\frac{{{\rm{ - }}T}}{{{\rm{17}}{\rm{.53949}}}}}} + 0.304\;41 $$ (6) $$ {k_{{\text{helium}}}} = 9.410\;47 + 0.876\;13T - 0.003\;19{T^2} + 1.011\;82 \times {10^{ - 5}}{T^3} - 1.272\;75 \times {10^{ - 8}}{T^4} $$ (7) $$ {\mu _{{\text{helium}}}} = {10^{ - 6}} \times (1.182\;81 + 0.128\;686T - 6.225\;11 \times {10^{ - 4}}{T^2} + 2.227\;24 \times {10^{ - 6}}{T^3} - 2.969\;36 \times {10^{ - 9}}{T^4}) $$ (8) $$ {P_{{\text{cold}}}} = \exp \left(6.444\;390\;9 - 50.334\;408{T^{0.5}} + 52.703\;82\frac{{\ln T}}{T}\right) $$ (9) 式中：$ {\rho _{{\text{helium}}}} $为氦气的密度；$ {k_{{\text{helium}}}} $为氦气的热导率；$ {\mu _{{\text{helium}}}} $为氦气的动力黏度；$ {P_{{\text{cold}}}} $为二级冷头制冷功率。
万能试验机拉伸杆、上部不锈钢腔壁、液氮管路和导线的漏热、铜屏顶部的气体导热和辐射漏热作为外部热源输入到模型中，由于腔外是10−3 Pa真空状态且试样腔外壁包裹多层绝热材料，因此试样腔与冷屏间辐射换热可以忽略不计。模型中试验腔的漏热分析如表5所列。模型的初始温度均为298 K，设置制冷机二级冷头的制冷功率为Pcold，漏热则以热通量形式从试验腔顶部边界输入，其余边界均为热绝缘界面。
表 5 模型中试验腔漏热分析Table 5. Heat load of test chamber in model漏热形式 漏热量/W 连接杆漏热 3.7 不锈钢壁漏热 4.02 液氮管路漏热 0.15 导线漏热 0.37 顶部气体导热 1.58 腔顶辐射漏热 1.04 剩余气体导热 0.15 总计 11.01 2.3 仿真结果及模型验证
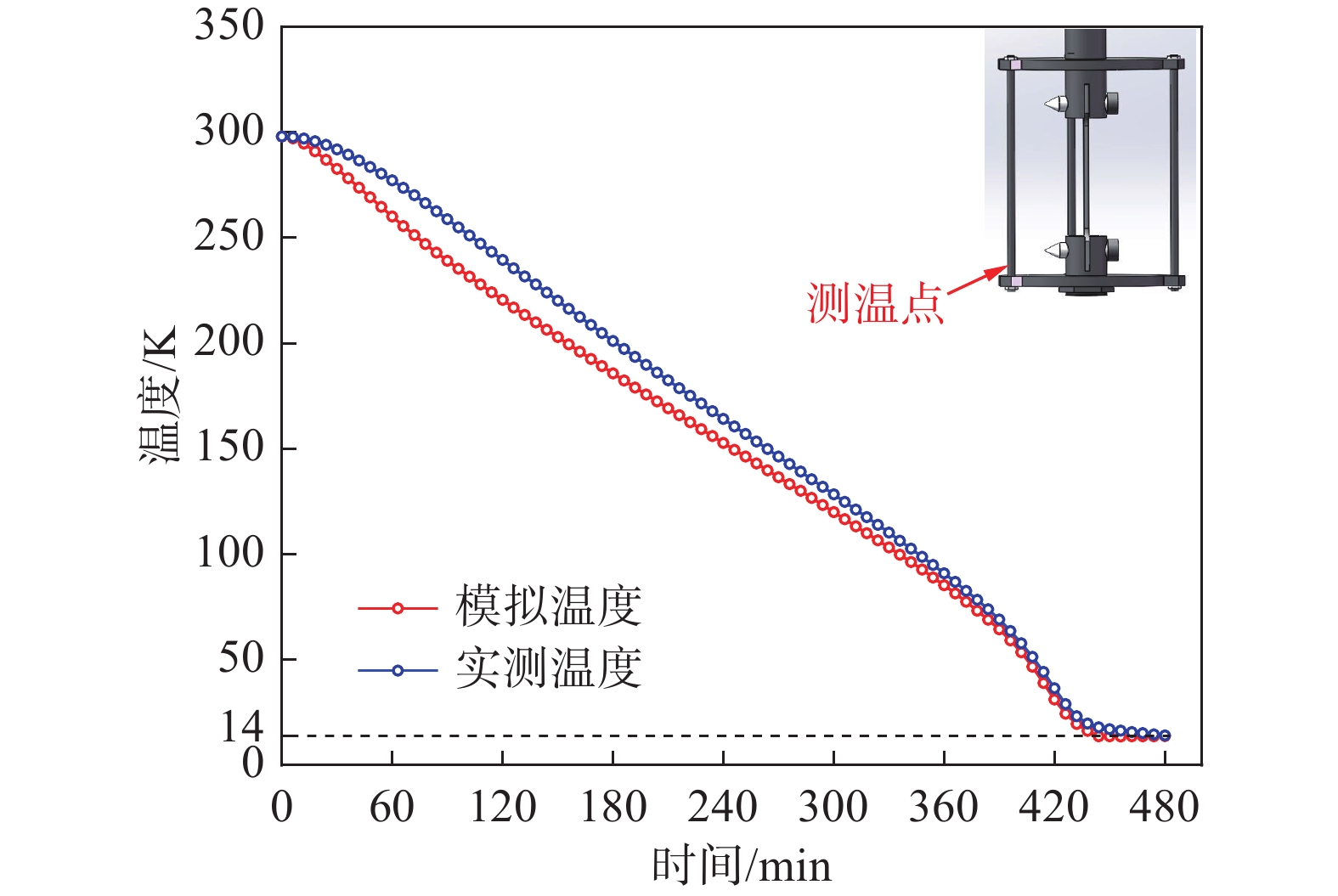
对模型中支撑架底部的温度进行记录并与实测的降温数据进行对比，如图8所示。可见仿真结果与实测数据趋势一致，在100~280 K温区最大偏差仅为7.8%，说明该模拟结果与实际降温情况具有较高的吻合度。
2.4 试件温度分布均匀性
利用验证后的仿真模型，图9给出了降温过程中试件平行段纵向和横向温度随时间的变化。
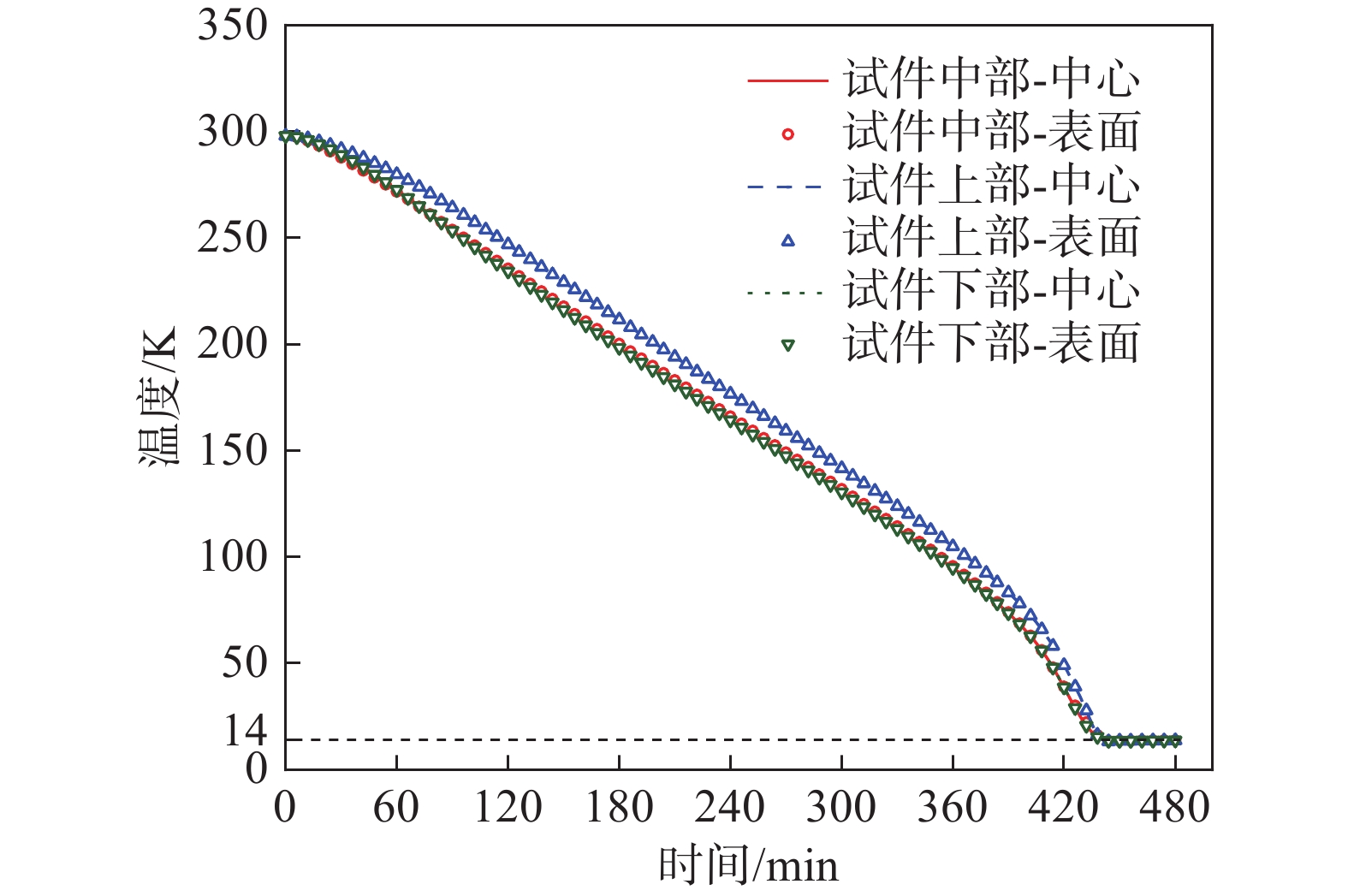
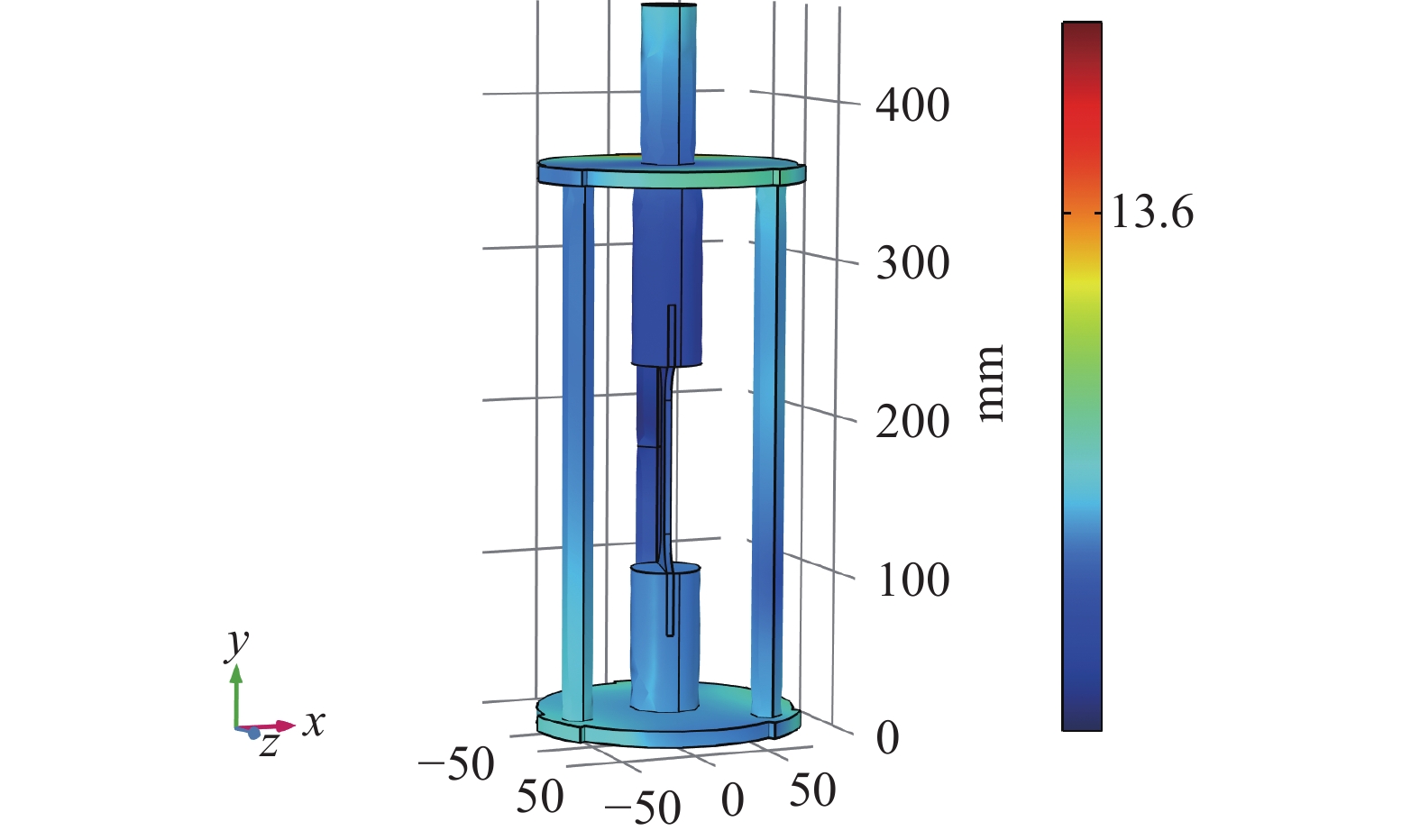
由图9表明，纵向方向上试件中下部的温度分布均匀性良好，同一时刻最大温差仅为1.94 K。由于支撑杆和上部腔体壁等漏热的影响，近乎整个降温过程中试件上部的温度明显高于中下部，同一时刻最大温差高达10 K。同一水平处，试件平行段在横向方向上的温度分布比较一致，同一时刻最大温差为1.8 K。这说明试件的温度分布在纵向上具有更为明显的差异，即试件的平行段长度对于试件温度均匀性的影响更大。7.5 h后试件平行段温度分布均匀，如图10所示，最大温差仅在0.1 K左右。
![]()
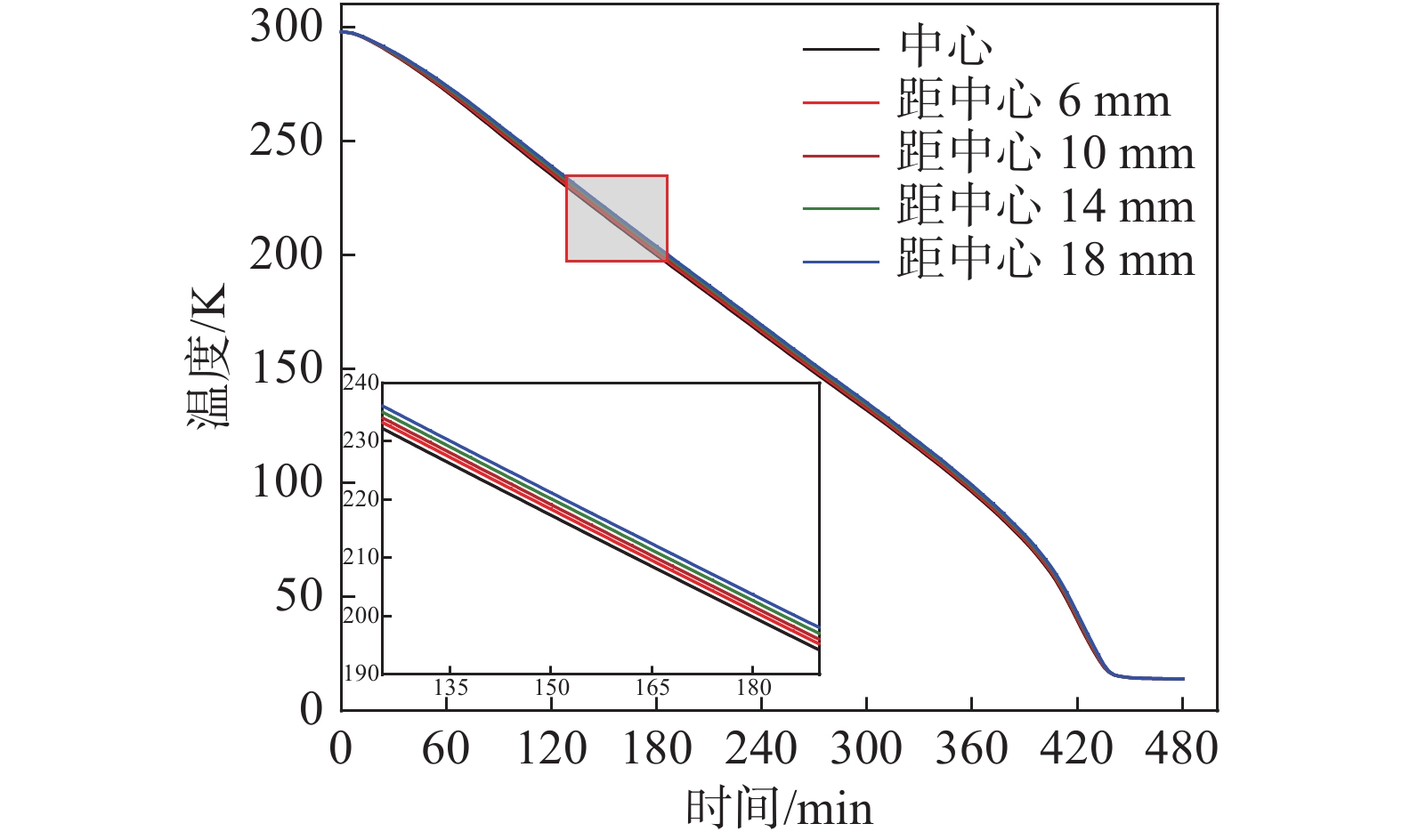
图 10 7.5 h时支撑杆与试件的温度分布情况Figure 10. Temperature distribution of support and specimen at 7.5th hour分别对距离试件中心6 mm、10 mm、14 mm和18 mm的位置进行温度探测并与中心处温度进行比较，如图11所示。这4个位置与中心的最大温差分别为1 K、1.8 K、2.9 K和3.9 K，考虑到试件被测段温度分布均匀性对测试结果的影响，采用本装置进行低温拉伸测试时，试件平行段总长应不超过20 mm。
![]()
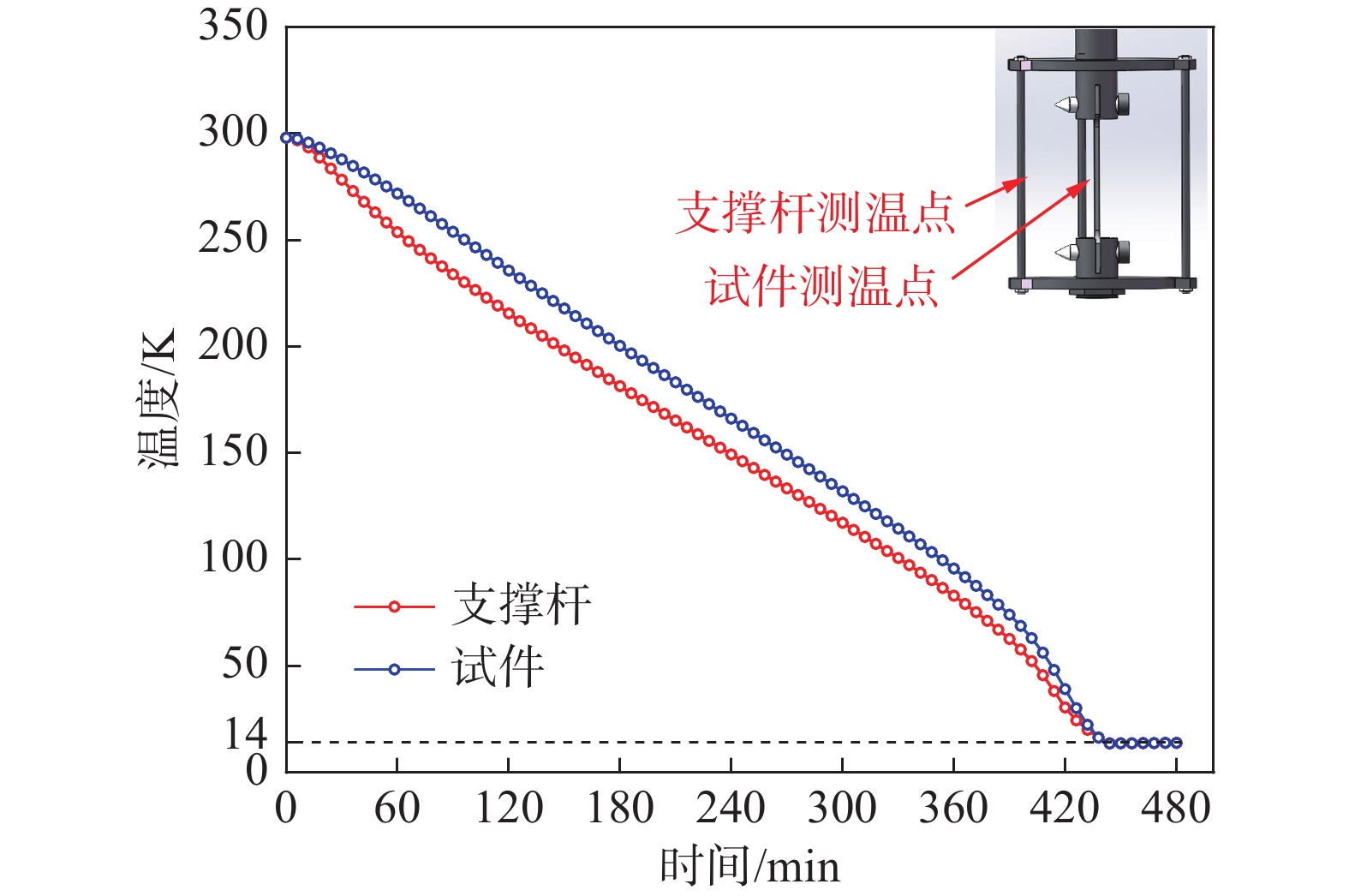
图 11 距中心不同距离处温度随时间变化情况Figure 11. Temperature variation with time at different distances from the center通常情况下，拉伸装置基本上都不会直接测试试件的温度（试件会被拉断）。本系统通过测试支撑杆竖直方向的温度来代表试件平行段的纵向温度分布。模拟结果显示，在50~300 K温区内支撑杆与试件表面的温度相差较大，同一时刻两者温度差在14 K左右，最大约20 K，如图12所示。
这是因为支撑杆底部测温点距离导热热桥更近，受冷头降温影响更加显著。由于氦气在低温下比热容较大而热导率较小，同一水平处试件温度的降低表现出迟滞性。延长保温时间是解决这一问题的首选方法。过往文献及测试者也都提及了这一点[6，15]。30~60 min的保温时间将有效减小温度计与实际试件中心点之间的温差，确保试件标距段温度到达目标温度。同时，在20 K以下温区，这一问题并不突出。
3. 测试装置功能验证
3.1 测试装置的可重复性验证
在297 K、77 K和20 K这3个温度工况下对316 L不锈钢进行拉伸测试来验证装置的重复性精度。所用拉伸试件为两端打孔的矩形截面试样，宽度为12.5 mm，厚度为4 mm。
试件在达到目标温度后，保温时间不少于30 min，待试件测试段温度稳定且分布均匀后开始进行拉伸测试，拉伸应变速率为3×10−4 s−1；测试结束后等待试验腔回温至接近室温时再打开腔体，防止空气中的水蒸气遇到腔内低温部件而发生严重的结霜、结露现象。
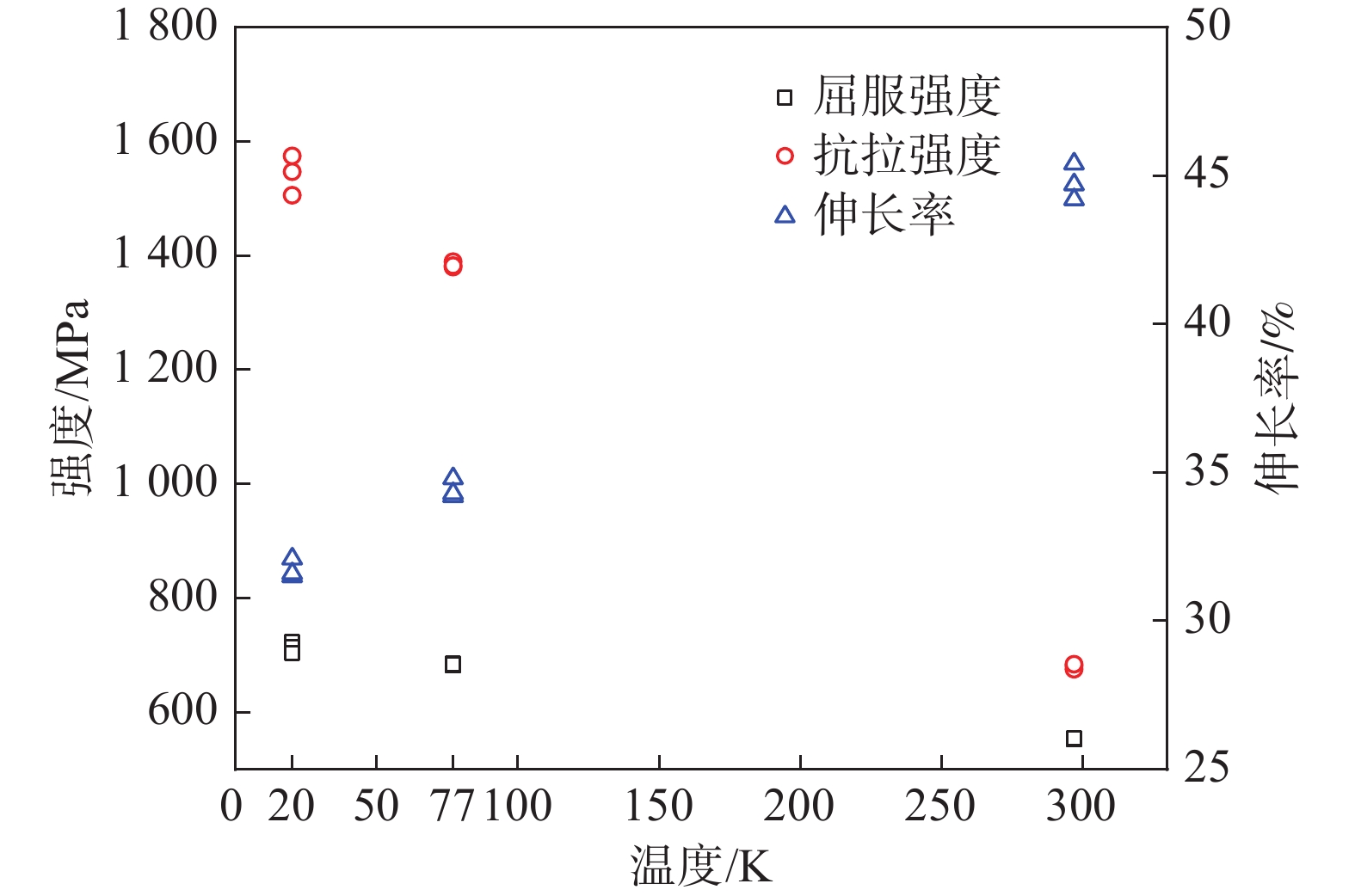
3个温度工况下316 L不锈钢试件的测试结果如图13所示。可见，同工况下的测试数据具有较高的吻合度。 20 K时的抗拉强度数据组呈现出最大的相对偏差，但也仅为4.7%，其余数据组的相对偏差均小于3%，最小的相对偏差仅为0.6%。经计算得，本测试装置的测量结果可重复性高达97.8%。
![]()
图 13 316 L不锈钢的拉伸测试数据可重复性验证Figure 13. Repeatability of tensile test data for 316 L stainless steel3.2 材料的测量结果与文献偏差分析
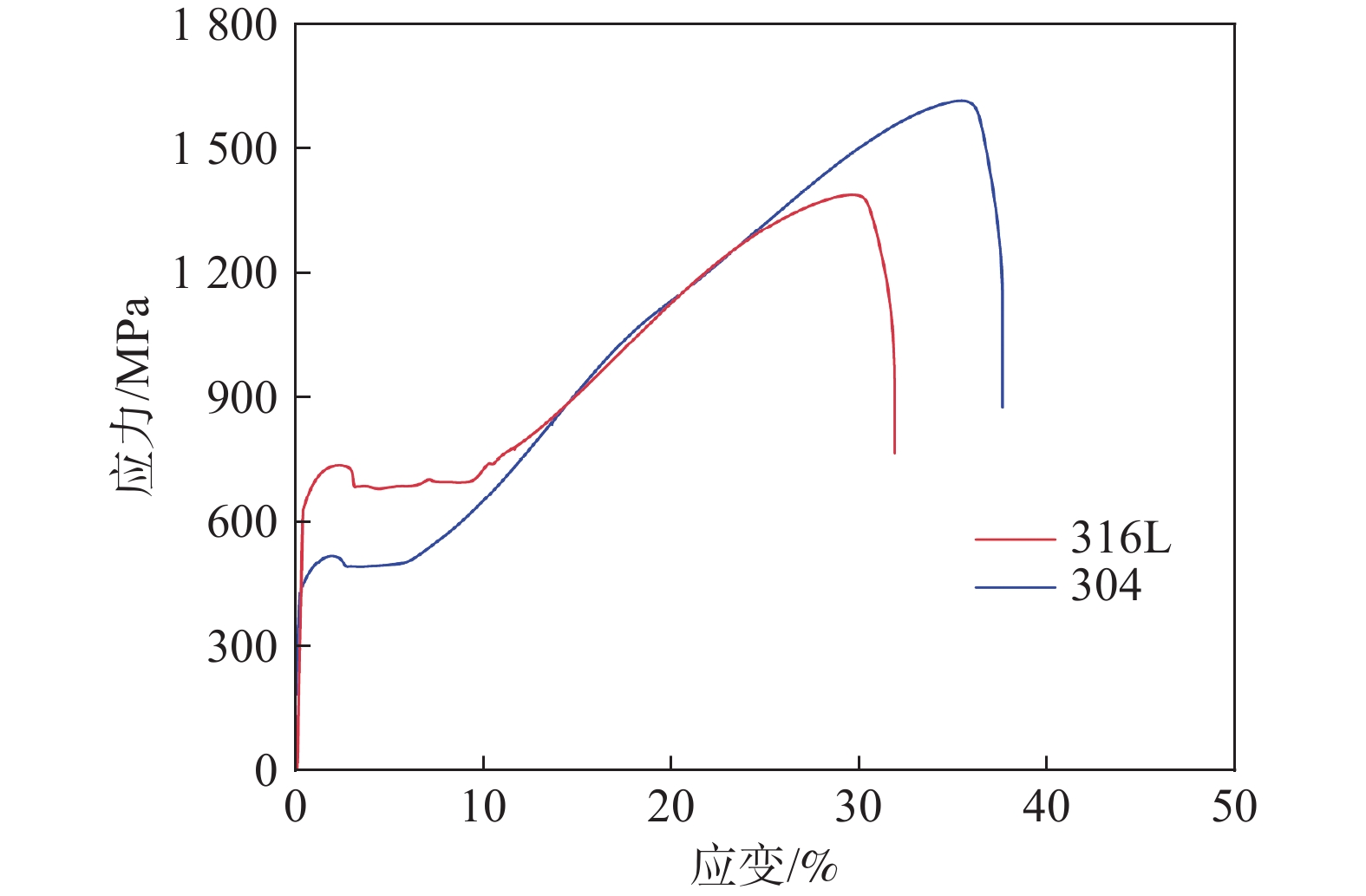
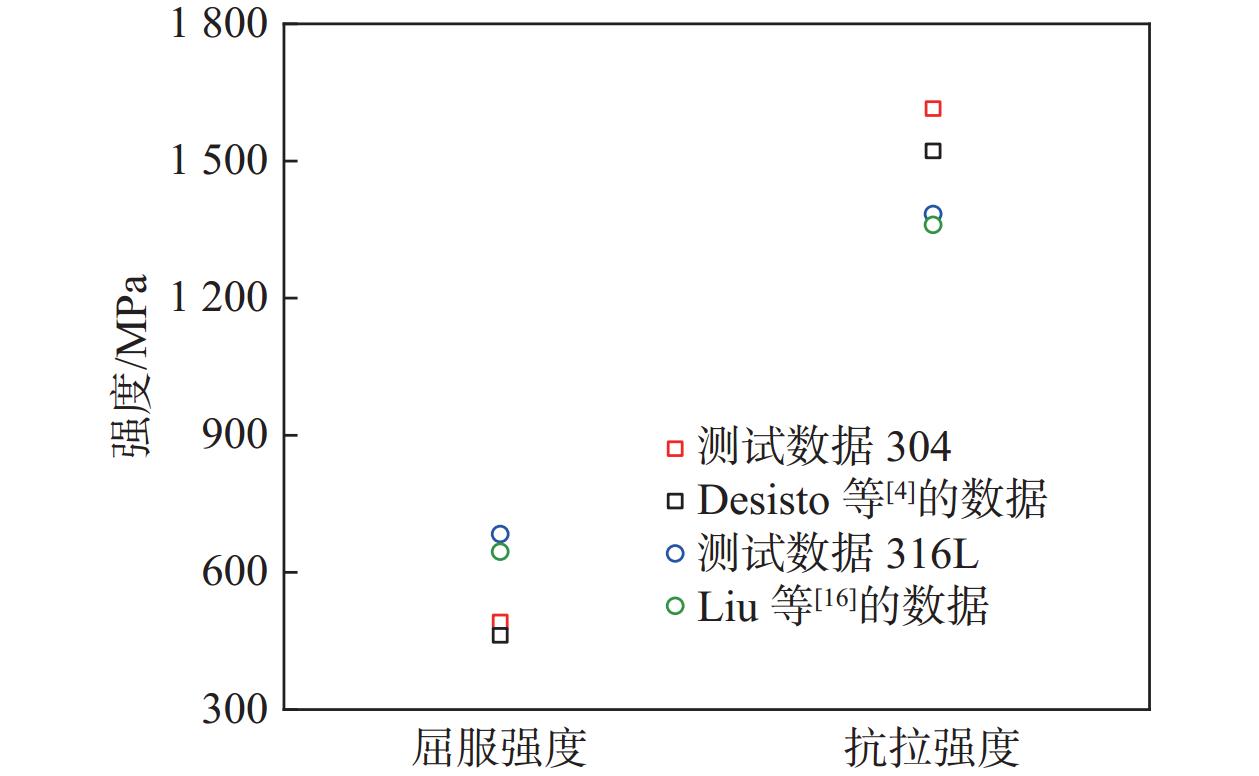
由于难以获得20 K温区的直接测量数据，以77 K为基准低温工况，选取304不锈钢和316 L不锈钢这两种常用低温典型材料进行拉伸测试，两种材料在77 K温度下的拉伸曲线如图14所示，并将测试所得数据与文献数据[4，16]进行对比，如图15所示。可见，本测试装置测得的304不锈钢和316 L不锈钢材料拉伸性能与文献数据吻合良好，最大偏差仅为6.3%。
![]()
图 14 304和316 L不锈钢在77 K温度下拉伸测试应力-应变曲线Figure 14. Tenslie test stress-strain curves of 304 and 316 L stainless steel at 77 K![]()
图 15 304不锈钢和316 L不锈钢测试数据与文献数据对比Figure 15. Comparison between present experimental data and literature data of 304 and 316 L stainless steel4. 结论
研制深冷温区材料拉伸测试装置，以G-M制冷机为冷源、以氦气为载冷介质，具备14~300 K大温区内材料拉伸性能测试能力。对腔内支撑架及试件的温度分布进行模拟，模拟结果显示试件纵向温度分布均匀性差，但横向没有表现出明显的温差。试件平行段长度不应超过20 mm，到达目标温度后应保温30~60 min。对316 L不锈钢在不同温度工况下拉伸性能进行多次重复测试，可重复性97.8%。同时对304不锈钢和316 L不锈钢在77 K温度下进行拉伸测试，测试数据与文献数据相比最大偏差和平均偏差分别为6.3%和3.9%，表明该测试装置具有良好的准确性，实现了深冷温区材料拉伸力学性能测试的功能要求。
-
![]()
图 1 低温拉伸测试装置系统组成图
1. 真空腔；2. 控温系统；3. 冷却系统；4. 真空抽气系统；5. 万能试验机龙门架；6. 移动横梁；7. 力传感器；8. 万能试验机底座。
Figure 1. Composition of low temperature tensile test system
![]()
图 2 真空腔三维结构图
1. 阀门操作区；2. 低温试验腔；3. 真空室；4. 冷屏；5. 导热热桥；6. G-M制冷机；7. 波纹管；8. 连接板；9. 通用力学试验机拉伸杆。
Figure 2. 3D Construction of cryogenic chamber
![]()
图 3 试验腔内部结构图
1. 连接板；2. 腔顶法兰；3. 隔热泡沫；4. 铜屏；5. 样品夹具；6. 样品；7. 拉伸试验工装；8. 液氮输送管路；9. 试验腔连接杆；10. 波纹管。
Figure 3. Internal Construction of test chamber
![]()
图 4 温度计布置示意图
1、2、3. PT1000温度计；4、5. 碳电阻温度计；6. 加热电阻；7. 试件。
Figure 4. Location of temperature sensors
![]()
图 5 实际降温测试的温度-时间变化曲线
Figure 5. The variation curves of temperature with in actual cooling test
![]()
图 6 有限元模型
1. 低温试验腔；2. 导热热桥；3. 制冷机二级冷头；4. 铜屏；5. 支撑杆；6. 试件；7. 万能试验机拉伸杆。
Figure 6. Finite element simulation model
![]()
图 10 7.5 h时支撑杆与试件的温度分布情况
Figure 10. Temperature distribution of support and specimen at 7.5th hour
![]()
图 11 距中心不同距离处温度随时间变化情况
Figure 11. Temperature variation with time at different distances from the center
![]()
图 13 316 L不锈钢的拉伸测试数据可重复性验证
Figure 13. Repeatability of tensile test data for 316 L stainless steel
![]()
图 14 304和316 L不锈钢在77 K温度下拉伸测试应力-应变曲线
Figure 14. Tenslie test stress-strain curves of 304 and 316 L stainless steel at 77 K
![]()
图 15 304不锈钢和316 L不锈钢测试数据与文献数据对比
Figure 15. Comparison between present experimental data and literature data of 304 and 316 L stainless steel
表 1 代表性低温力学性能测试装置
Table 1 Representative mechanical property test device at low temperature
冷源 测试温度/K 单次测试消耗/降温时间 测试样品 参考文献 液氦 4.2 5 L液氦、3 L液氮 302不锈钢等 DeSisto等[4] 液氢 20 140 L液氢 6061-T6铝合金 Belton等[5] 液氦 4.2 \ 聚苯乙烯 Foley等[8] 液氦 4.2 10~12 L 2024-T8铝合金 Kaufman等[9] 液氦、液氮、酒精干冰 4.2、77、195 \ 25Mn5Cr1Ni钢 陈国邦[10] 液氢、气氦 20 \ 304 L等 Deimel等[11] G-M制冷机 4.2~300 20 h以上 S30408钢 姜恒等[6] G-M制冷机 8~300 14 h 5A06铝合金 谢世永等[7] 
下载: 导出CSV
表 2 最低温度时试验腔漏热分析
Table 2 Heat load of test chamber at lowest temperature
漏热形式 漏热量/W 拉伸杆漏热 3.73 不锈钢壁漏热 4.02 液氮管路漏热 0.15 导线漏热 0.37 剩余气体导热 0.15 筒体辐射漏热 15.7 总计 24.12
下载: 导出CSV
表 3 误差计算数据
Table 3 Error calculation data
误差项 误差值/% $ \dfrac{{\delta {F_T}}}{{{F_T}}} $ ±0.5 $ \dfrac{{\delta {W_{293}}}}{{{W_{293}}}} $ ±0.08 $ \dfrac{{\delta {D_{293}}}}{{{D_{293}}}} $ ±0.25 $ \dfrac{{\delta \left( {d{L_T}} \right)}}{{d{L_T}}} $ ±0.006 $ \dfrac{{\delta {L_{293}}}}{{{L_{293}}}} $ ±0.02 $ \dfrac{{\delta T}}{T} $ ±0.67 $\dfrac{ {\Delta \sigma } }{\sigma }$ ±0.92 $\dfrac{ {\Delta \varepsilon } }{\varepsilon }$ ±0.67
下载: 导出CSV
表 4 紫铜热导率计算公式系数
Table 4 Copper thermal conductivity calucation formula coefficient
系数 取值 系数 取值 系数 取值 a 1.8743 d 0.13294 g −0.0051276 b −0.41538 e 0.26426 h 0.0014871 c −0.6018 f −0.0219 i 0.003723
下载: 导出CSV
表 5 模型中试验腔漏热分析
Table 5 Heat load of test chamber in model
漏热形式 漏热量/W 连接杆漏热 3.7 不锈钢壁漏热 4.02 液氮管路漏热 0.15 导线漏热 0.37 顶部气体导热 1.58 腔顶辐射漏热 1.04 剩余气体导热 0.15 总计 11.01
下载: 导出CSV
-
[1] DUTHIL P. Material properties at low temperature[R]. CERN Yellow Report CERN-2014-005,2015:77-95.
[2] KIM M S,LEE T,SON Y,et al. Metallic material evaluation of liquid hydrogen storage tank for marine application using a tensile cryostat for 20 K and electrochemical cell[J]. Processes,2022,10(11):2401. doi: 10.3390/pr10112401
[3] 吴英哲,赵钦宇,甘智华,等. 材料低温力学性能测试技术研究进展[J]. 低温工程,2021(5):18−27. doi: 10.3969/j.issn.1000-6516.2021.05.004 [4] DESISTO T S,CARR L C. Low temperature mechanical properties of 300 series stainless steel and titanium[C]//Advances in Cryogenic Engineering,Boston,MA:Springer US,1961:577-586.
[5] BELTON J,GODBY L,TAFT B. Materials for use at liquid hydrogen temperature[C]//Symposium on Low-Temperature Properties of High-Strength Aircraft and Missile Materials,West Conshohocken,PA:ASTM International,1961:108-121.
[6] 姜恒,陈学东,范志超,等. 金属材料低温深冷拉伸试验装置的研制[J]. 低温与超导,2018,46(6):11−15. doi: 10.16711/j.1001-7100.2018.06.003 [7] 谢世永,赵春宇,张连万,等. 单台G-M制冷机为冷源力学性能测试系统研究[J]. 低温工程,2022(1):1−4,16. doi: 10.3969/j.issn.1000-6516.2022.01.001 [8] FOLEY R J,JELINEK F J. Low temperature thermal and mechanical properties of polystyrene and polyethylene foams[EB/OL]. United Kingdom,1974 [2023-08-31] .https://www.osti.gov/biblio/4178824.
[9] KAUFMAN J G,BOGARDUS K O,WANDERER E T. Tensile properties and notch toughness of aluminum alloys at −452°F in liquid helium[C]//Advances in Cryogenic Engineering,Boston,MA:Springer US,1995:294-308.
[10] 陈国邦. 奥氏体不锈钢的低温拉伸试验[J]. 低温与特气,1984(4):52−56. [11] DEIMEL P,SATTLER E. Austenitic steels of different composition in liquid and gaseous hydrogen[J]. Corrosion science,2008,50(6):1598−1607. doi: 10.1016/j.corsci.2008.02.024
[12] POWELL R L,ROGERS W M,RODER H M. Thermal conductivities of copper and copper alloys[J]. Advances in Cryogenic Engineering,1956(2):166−171.
[13] HANDS B A,ARP V D. A correlation of thermal conductivity data for helium[J]. Cryogenics,1981,21(12):697−703. doi: 10.1016/0011-2275(81)90211-3
[14] ARP V D,MCCARTY R D,FRIEND D G. Thermophysical properties of helium-4 from 0.8 to 1 500 K with pressures to 2 000 MPa,NIST-TN/1334[R]. Washington,DC:NASA,1989.
[15] PARK W S,YOO S W,KIM M H,et al. Strain-rate effects on the mechanical behavior of the AISI 300 series of austenitic stainless steel under cryogenic environments[J]. Materials & Design,2010,31(8):3630−3640.
[16] LIU H J,WU Y,HAN Q Y,et al. Mechanical tests on the ITER PF 316L jacket after compaction[J]. Cryogenics,2011,51(6):234−236. doi: 10.1016/j.cryogenics.2010.06.017
计量
- 文章访问数: 33
- HTML全文浏览量: 14
- PDF下载量: 19
