Performance Testing and Optimization Layout Improvement Analysis ofMulti-layer Insulation Materials for Space
-
摘要:
多层隔热材料在空间高真空环境下具有优良的绝热性能，随着空间技术的发展，对液氢温区多层绝热材料提出了更高的绝热性能和阻燃等特殊要求。基于层与层计算方法建立了多层绝热材料热流密度的计算模型，选取40层、60层和70层三种常用层数绝热材料对其热流密度进行了测试与计算，分析了层密度、冷热边界条件等对多层绝热材料热流密度的影响。最后通过遗传算法分析了多层绝热材料的布置方式对绝热性能的影响，获得了液氢温区绝热材料优化布置方式，与等密度多层绝热材料布置方式相比，热流密度降低10.63%。
Abstract:Multi-layer insulation materials have strong insulation performance in high vacuum environments. With the development of space technology, special requirements have been put forward for the insulation performance of multi-layer insulation materials applied in the liquid hydrogen temperature range, such as higher insulation performance and flame retardancy. A calculation model for the heat flux of multi-layer insulation materials is established based on the layer by layer calculation method. Three commonly used layers of insulation materials, namely 40 layers, 60 layers, and 70 layers, are selected for testing and calculating their heat flux. The effects of layer density, cold and hot boundary conditions on the heat flux of multi-layer insulation materials are analyzed. Finally, the impact of the arrangement of multi-layer insulation materials on insulation performance is analyzed through genetic algorithm, and an optimized arrangement method for insulation materials in the liquid hydrogen temperature range is obtained. This arrangement method can reduce the heat flux by 10.63% compared to the equal density multi-layer insulation material arrangement method.
-
Keywords:
- multi-layer insulation /
- heat flux /
- optimize layout
-
0. 引言
液氢（LH2）、液氧（LO2）和液态甲烷（LCH4）等低温液体不仅是地面能源行业的重要燃料，也是航天器和运载火箭的首选推进剂[1]。为了获得更大的体积能量密度，这些低温液体在极端低温的条件下以饱和甚至过冷的状态储存，会导致相当大的热量从外部环境泄漏至低温储罐中。储罐的漏热会导致低温液体持续蒸发，进而导致储罐超压或推进剂排气损失[2-5]。因此，低温储罐的高效隔热技术是未来月球和火星探测等长期任务的关键技术。目前人们在了解高真空环境下的隔热性能方面做了大量工作，开发了多层绝热材料[6]（Multi Layer Insulation，MLI）。
本文对应用于空间的高性能多层绝热材料的优化布置方式及性能影响进行了分析。多层绝热材料结构由交替的反射层和间隔层组成，其内部传热分为辐射换热、残余气体导热和固体导热[7]。多层绝热材料的反射层通常由具有高反射率和低发射率的材料制成或涂覆，故而来自前一层的辐射热可以被当前层的辐射屏部分反射，而剩余的能量转移到下一层再次被反射。间隔层主要由低热导率的材料组成，如玻璃纤维、尼龙、丝网和泡沫等，降低相邻反射层间的固体导热。多层绝热材料多应用在高真空环境，避免了对流换热[8]。国内外对于多层绝热材料的研究已趋于成熟，主要以镀铝聚酯薄膜作为反射层，涤纶网作为间隔层[9]。针对液氢储罐中多层绝热材料需要具有较小的热流密度和阻燃性[10]等特殊要求，本文以铝箔作为反射层，玻璃纤维布作为间隔层进行实验及模拟，分析多层绝热在不同条件下的热流密度变化。此外通过遗传算法模拟求解在外界条件（如冷热边界温度、真空度等）相同、多层绝热材料数量相同的情况下的间隔层与反射层的优化布置方式。
1. 热流密度计算模型
对于多层绝热材料的热流密度的计算目前常见层与层模型（Layer-by-Layer）与洛克希德模型[11] 两种算法。两种方法虽均可求解多层绝热材料的热流密度，但洛克希德模型无法求解多层绝热材料的层间温度分布，且计算依赖于各材料的经验系数，故本文采用层与层模型进行多层绝热材热流密度的计算。
在层与层模型中，多层绝热材料的传热过程被分离为间隔物的固体导热（qs）、气体导热（qg）和辐射传热（qr）三个部分，并假定三种传热部分互不干扰。则多层绝热系统通过第i层的总热流密度（qtot，i）的计算公式为[7]：
$$ {q}_{\mathrm{t}\mathrm{o}\mathrm{t},i}={q}_{\mathrm{r},i}+{q}_{\mathrm{g},i}+{q}_{\mathrm{s},i} $$ (1) 式中：qtot.i为通过多层绝热结构的总热流密度；qr.i为通过多层绝热结构的辐射热流密度；qg，i为通过多层绝热结构的气体导热热流密度；qs，i为通过多层绝热结构的固体传热热流密度。
其中辐射传热部分认为多层绝热材料的层间间隔物对反射无影响，则相邻辐射层之间的辐射换热可表示为式：
$$ {q}_{\mathrm{r},i}=\frac{\sigma \left({T}_{i+1}^{4}{-T}_{i}^{4}\right)}{\dfrac{1}{{\varepsilon }_{i}+1}+\dfrac{1}{{\varepsilon }_{i}}-1} $$ (2) 式中：Ti+1为温度较高侧辐射屏的温度；Ti为温度较低侧辐射屏的温度；εi+1为温度较高侧辐射屏的发射率，εi为温度较低侧辐射屏的发射率，对于铝箔，参考文献[10]的数据；$ \sigma $为玻尔兹曼常数。
气体导热qg，i为：
$$ {q}_{\mathrm{g},i}={C}_{1}p\alpha （{T}_{i+1}-{T}_{i}） $$ (3) $$ C_1=\frac{\dfrac{\gamma+1}{\gamma-1}}{\left(\dfrac{R}{8\text{π}MT}\right)^{\frac{1}{2}}} $$ (4) 式中：p为相邻反射层之间的气体压力；α为适应系数，对于空气α=0.9；R为气体常数；M为气体的摩尔质量；T为反射层表面的温度；γ=cp/cv，cp为等压比热容，cv为等容比热容；C1为气体导热项经验参数，对于空气C1=1.1666。
固体导热qs，i为：
$$ q_{\mathrm{s},i}=K_{\mathrm{S}}\left(T_{i+1}-T_i\right) $$ (5) $$ K_{\rm{S}}=C_2fk $$ (6) 式中：C2为经验常数，与间隔物材料的种类有关；f为间隔材料的稀松程度；k为两辐射层间隔材料的热导率。间隔材料为玻璃纤维布，其热导率KS参考文献[7]的数据。
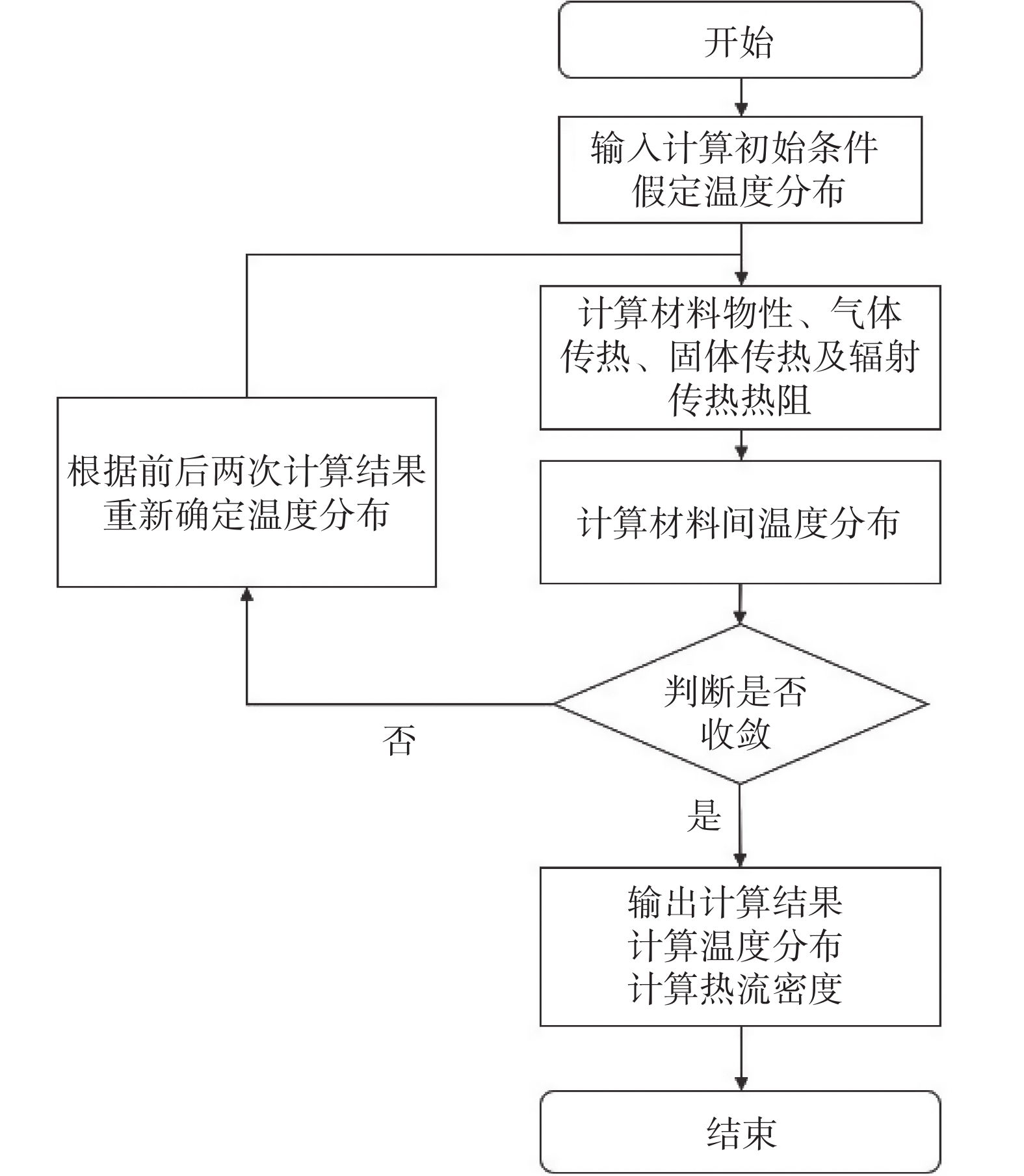
采用层与层模型，求解多层材料热流密度采用迭代算法。具体的求解流程如图1所示，首先沿绝热层厚度方向假定一个线性的温度分布，然后据此求解相邻两辐射层之间的热阻，再通过求得的热阻计算出新的温度分布，完成一个迭代周期。该过程一直进行到前后两次温度分布满足一定的收敛条件（收敛条件为前后两次温度分布小于0.001 K）[7]。其中完成一个周期后下一次迭代的温度分布可以由式（7）求出：
![]()
图 1 层与层模型求解多层绝热材料热流密度计算流程Figure 1. Calculation process for heat flux of multi-layer insulation materials using layer and layer model$$ T_n=T_{\mathrm{c}}+\frac{\displaystyle\sum_{i=1}^nR_i}{\displaystyle\sum_{i=1}^NR_i}\left(T_N-T_{\mathrm{c}}\right) $$ (7) 式中：Ri是第i−1层和第i层之间的热阻；N为总的层数；n为当前层的编号；TN为冷边界温度；Tc为热边界温度；Tn为第n层温度。
2. 实验装置及测试方法
2.1 实验测试装置及原理
多层绝热材料性能实验测试装置可对不同的绝热材料的热流密度进行测试，装置如图2所示。
![]()
图 2 多层绝热材料性能实验测试装置Figure 2. Schematic diagram of experimental testing device for multi-layer insulation material performance实验测试装置包括：量热器、真空系统、流量测量系统和温度测控系统。量热器包括：保护段加排液口、测量段加排液口、量热器内筒、量热器外筒、上保护段、测量段、下保护段及被测绝热材料。其中上保护段和下保护段充当等温保护器，以避免热量从两端泄漏到测量段中。进入测试容器的所有热量都只通过测量段侧壁，即被测材料的包裹处，测量段轴向上的温度梯度可以视为零。温度测量系统采用铂电阻温度计测量冷边界温度和热边界温度。流量测量系统使用湿式流量计，测量蒸发出的气体流量。
实验通过热流量法测试材料热流密度大小。在实验装置中冷热两侧热量传递仅通过多层绝热材料，通过测量以液氮为测量工质的量热器蒸发的气体流量，进而计算多层绝热材料热流密度大小[12]。
2.2 实验数据处理
2.2.1 多层绝热材料的漏热量计算
多层绝热材料的漏热量按式（8）计算。
$$ Q=VL{\rho }_{\mathrm{g}}\left(\frac{{T}_{0}}{{T}_{1}}\right)\left(\frac{{p}_{1}}{{p}_{0}}\right) $$ (8) 式中：Q为量热器漏热量；V为流量计采集的平均气体流量；L为液氮的汽化潜热；$ {\rho }_{\mathrm{g}} $为273.15 K下氮气的密度；p1为流量计出口处压力平均值；T1为流量计出口处温度平均值；p0为标准状态下的绝对压力；T0为标准状态下的热力学温度。
2.2.2 多层绝热材料的热流密度计算
多层绝热材料的热流密度q按式（9）计算。
$$ q=\frac{Q\mathrm{ln}\left(\dfrac{r+\delta}{r}\right)}{2\text{π}l\delta} $$ (9) 式中：r为量热器内筒的外半径；$ \delta $为多层绝热材料包裹的厚度；$ l $为量热器内筒的测量筒长度。
将实验测得的结果代入式（8）（9）即可计算出多层绝热材料样品的漏热量及热流密度。
3. 结果分析与讨论
3.1 实验与计算结果对比分析
对三种布置方式的多层绝热材料进行实验测量及模拟计算所得热流密度如表1所列。通过层与层模型，多层绝热材料的布置方案为1、2、3时模拟热流密度分别为1.93 W/m2、1.58 W/m2、1.41 W/m2。相较于实验所得热流密度分别为2.11 W/m2、1.64 W/m2、1.43 W/m2，误差分别为8.49%、3.38%、1.60%，误差整体较小。其中方案1计算与实验的热流密度的误差增大到8.49%，但实际两者数值误差仅为0.18 W/m2，证明了层与层模型计算的合理性。多层绝热材料的误差随层数的增加逐渐减少，这主要是因为层数及层密度的增加会导致层间气体导热难以下降以影响计算的准确性。
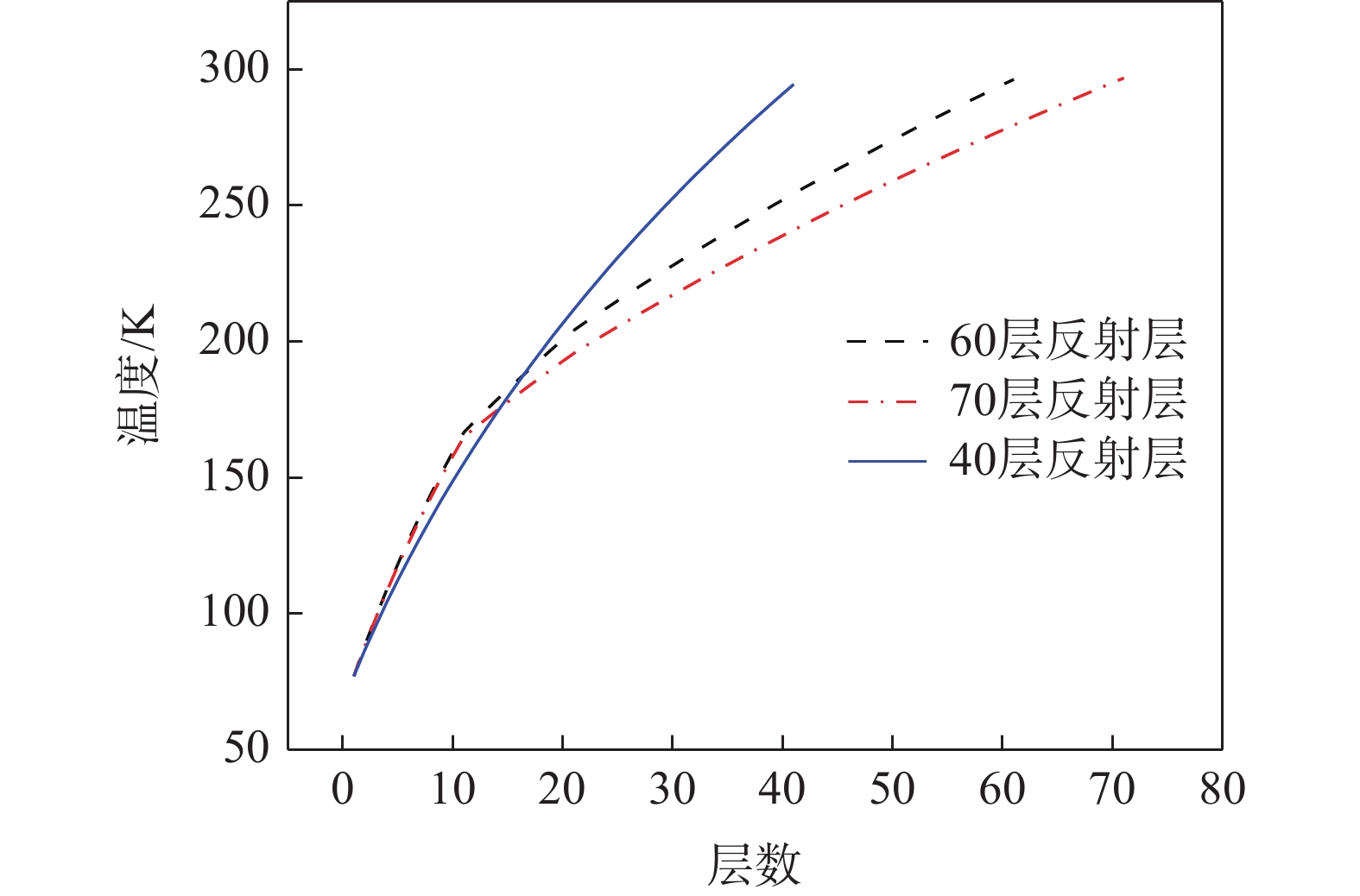
表 1 三种多层绝热材料实验及模拟热流密度Table 1. Experimental and simulated heat flux of three multilayer insulation materials方案 实验热流密度/（W/m2） 模拟热流密度/（W/m2） 误差/% 1 2.11 1.93 8.49 2 1.64 1.58 3.38 3 1.43 1.41 1.60 三种方案的多层绝热材料温度随层数的分布情况如图3所示。可以看出，三种方案的内部温度沿层数变化的趋势是一致的，即在低温段的斜率均大于在高温段斜率，由傅里叶定律可知多层绝热材料在低温侧的导热系数更小。方案2、3在10层及20层部分存在转折点主要是因为层密度的变化导致了温度梯度的突变。而在20层至30层的温度梯度变化不大，是因为实验仪器的真空夹层尺寸限制，层密度变化不大以致温度梯度几乎无变化。
![]()
图 3 三种布置方案在不同层数处的温度分布曲线Figure 3. Temperature distribution curves of three layout schemes at different levels3.2 层密度对热流密度变化的影响
固定多层绝热材料反射层数为30层，冷热边界温度分别为77 K、300 K，压力恒定为7×10−4 Pa。当层密度从10层/cm增加至40层/cm的过程中热流密度的变化如图4所示。由图可见在层密度降低的情况下，热流密度随之降低，需要注意的是虽然层密度的降低会带来热流密度的降低，但过低的层密度会使得在容器外包裹的多层绝热材料易于脱落，从而影响使用。
![]()
图 4 多层绝热材料层密度变化对热流密度的影响Figure 4. The effect of density changes in multi-layer insulation materials on heat flux density3.3 热边界温度对热流密度的影响
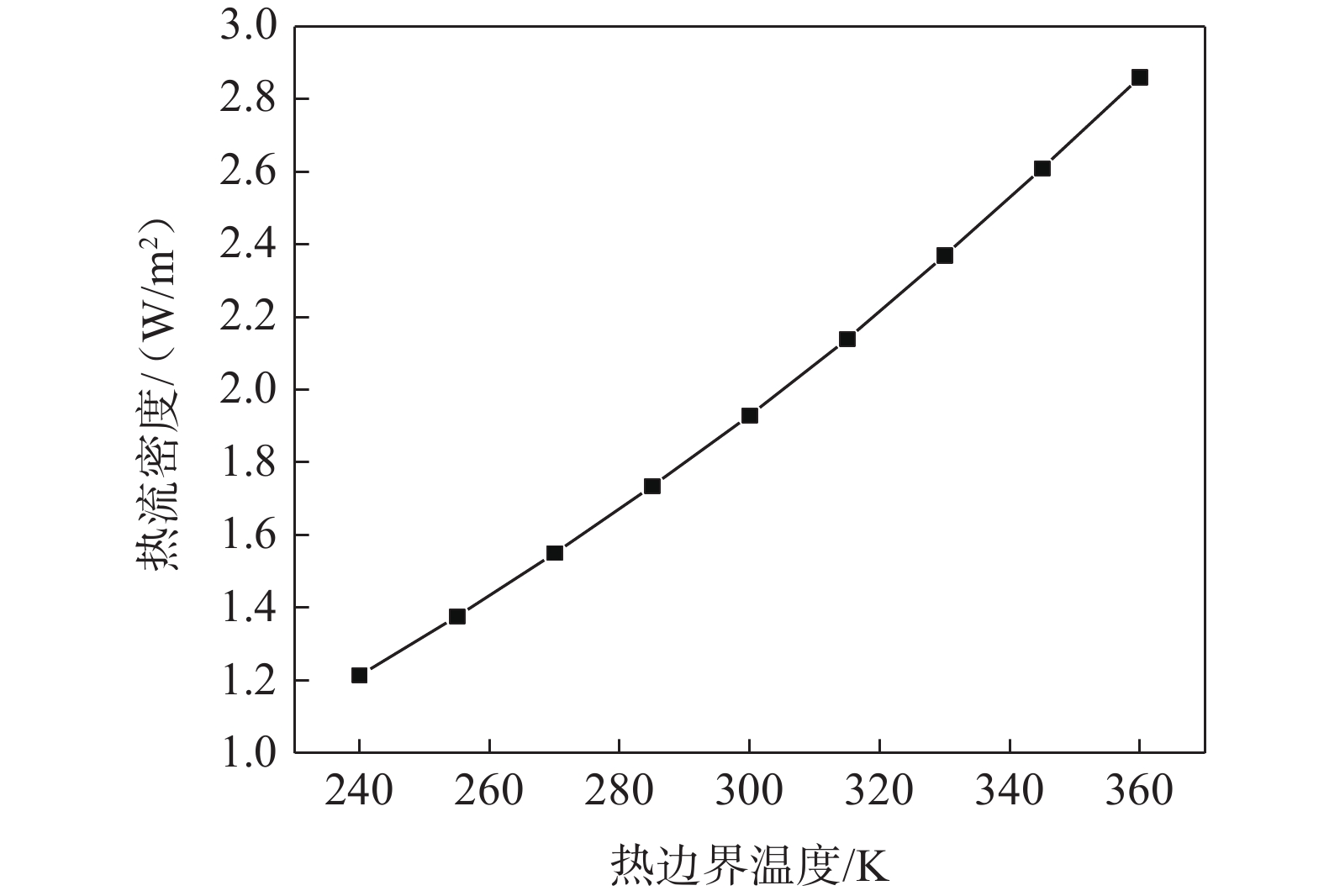
在实际使用环境中，多层绝热材料的热边界温度会随着环境温度变化而变化，需要考虑热边界温度与热流密度的变化关系。当压力恒定为7×10−4 Pa，冷边界温度77 K，其他条件保持不变的情况下，热边界温度由240 K升高至360 K时，热流密度变化如图5所示。温度由240 K升高至360 K的过程中，热流密度由1.21 W/m2升高至2.86 W/m2。热边界温度升高会导致热流密度的升高，但两者的关系为非线性，这主要是因为间隔材料及反射层材料的物性参数是随温度变化的非线性函数，故而影响热流密度的变化。
![]()
图 5 多层绝热材料热边界温度变化对热流密度的影响Figure 5. Effect of thermal boundary temperature changes on heat flux density of multilayer insulation material3.4 层数对多层绝热材料的影响
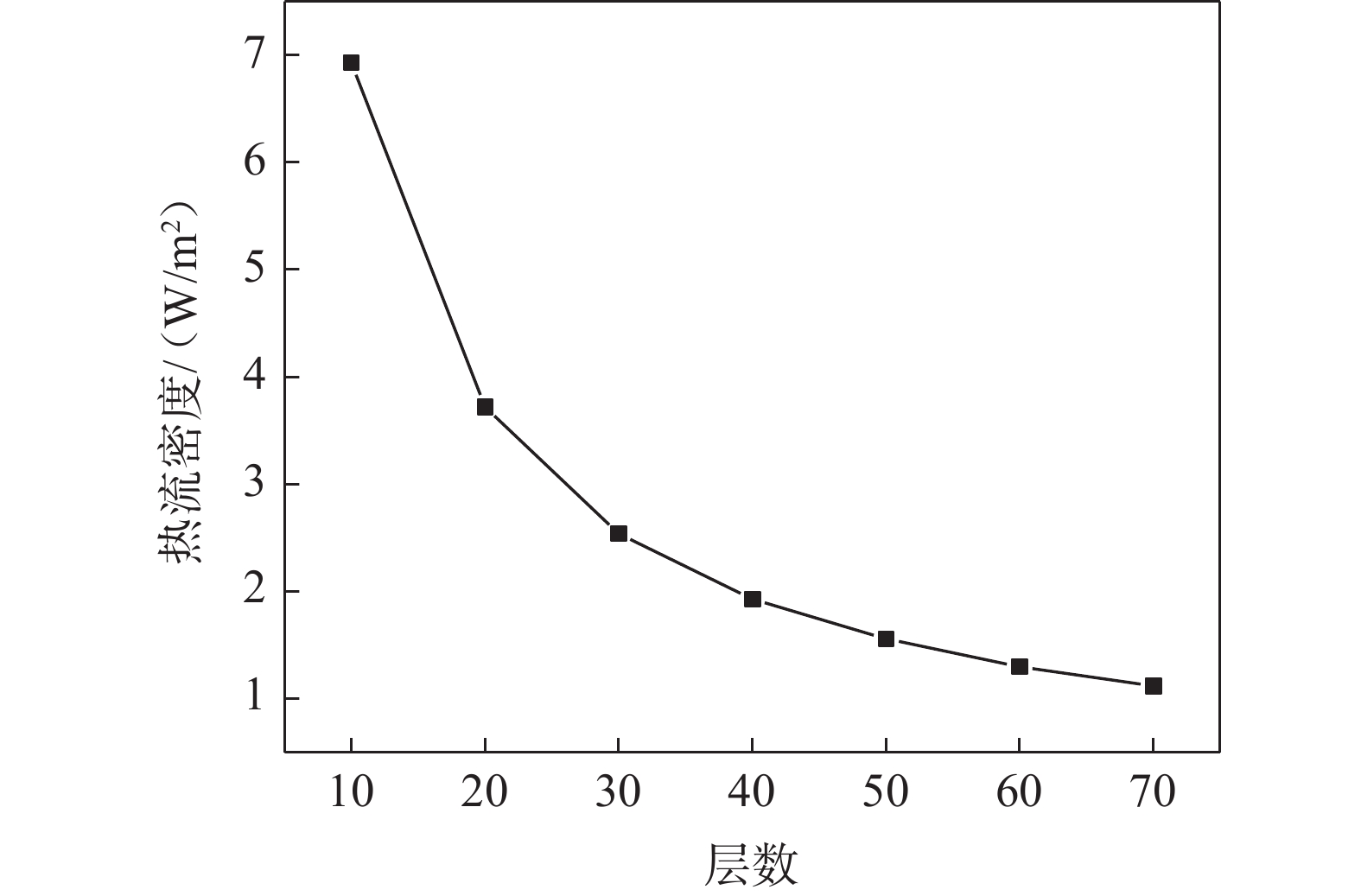
层密度为18.1层/cm，热边界温度300 K，压力7×10−4 Pa，不同层数下的热流密度变化如图6所示。可以看出，随着层数的增加，热流密度逐渐变小，但曲线的斜率也在逐渐变小。层数由总10层增加至20层时，热流密度由6.93 W/m2降低至3.72 W/m2，降低了46.3%，但总层数由60层增加至70层时，热流密度由1.3 W/m2降低至1.12 W/m2，降低了13.8%。可见随着层数的增加，热流密度的降低速率会减少。因此，在需要考虑空间材料的体积及质量等实际应用中，漏热量并不是越少越好，需要综合考虑。层数增多造成体积和质量的增加，应考虑实际的漏热量需求及多层绝热材料的层数、层密度等相关因素求解优化的分布。
![]()
图 6 多层绝热材料层数变化对热流密度的影响Figure 6. The effect of changes in the number of layers of multi-layer insulation materials on heat flux在高真空及冷边界温度一定的条件下，通过分析热边界温度、层密度、总层数等因素与多层绝热材料热流密度的变化关系，发现在材料选取时应考虑多层绝热材料的运行环境及实际漏热量需求。传统的多层绝热材料的技术已经比较成熟，但在实际使用时常将多层绝热材料当作一个整体分析而较少考虑层密度在径向上的变化。在实际使用时，多层材料的层数、层密度等受到材料的质量及体积的限制，冷热边界温度随外界环境温度变化而变化，而在材料的质量、体积、环境温度等因素限定的情况下，对多层材料性能的优化主要集中在对多层绝热材料的布置方式优化。Hedayat 等[13]首先提出了变密度多层绝热的概念，并通过分析认为变密度多层绝热材料应在固体导热量较大的部分增加间隔层材料，在何位置增加间隔层材料及增加多少间隔材料仍需明确。为解决以上两个问题，本文采用遗传算法进行求解。
4. 多层材料优化布置方式分析
4.1 遗传算法求解优化布置方式
遗传算法是模拟自然界生物进化机制的一种算法[14]。本文拟采用遗传算法来求解多层绝热材料的优化布置方式。
模拟假设条件：（1） 多层绝热材料中每层间隔层厚度一致（即预紧力相同）。（2）冷热边界温度不变，真空度不变。在进行计算时，模拟将m层间隔层均匀等密度排布后在其中插入n层反射层，每两层反射层间间隔层数为z层（z≠0），再通过遗传算法求解优化反射层与间隔层的分布，以求解多层绝热材料的优化布置方式。
步骤如下：
（1） 初始化模型参数。设置群体大小100，交叉概率0.9，变异概率0.05，算法终止的循环次数为1000次。
（2） 在总反射层数和间隔层数固定的情况下随机生成100种不同的多层绝热材料布置方式，并通过层与层模型计算对应热流密度。
（3） 计算每种布置方式的热流密度，并在100个不同的多层材料模型中去除10个热流密度最大的个体，即选择剩余90个个体进入下一代。
（4） 交叉变异。群体中剩余的90个个体以0.9及0.05的概率进行随机交叉和变异，使子代个体分别具有父代个体的某些特征，得到新的布置方式。
（5） 计算个体中的最低热流密度，并重新插入10组布置方式。重复上述3~5步骤直至达到迭代次数并每次迭代的最小热流密度不变。
需要注意的是遗传算法作为优化算法，只能求解问题的近似解而不是最优解。在间隔层固定为60层，反射层为30层的情况下使用遗传算法对多层绝热材料的优化布置求解10次。求解结果为：布置方式2为1~8层反射层处每两层反射层间间隔层层数固定为3层（z=3），9~22层反射层处每两层反射层间间隔层层数固定为2层（z=2），23~30层处每两层反射层间间隔层层数固定为1层（z=1）。对比布置方式2、7、8，虽然不同布置方式的层数分布方式有所区别，但整体趋势变化不大，且热流密度分别为2.3137 W/m2、2.3156 W/m2、2.3172 W/m2，三者间最大误差小于0.005 W/m2。使用遗传算法求解多层绝热材料的优化布置是可行的。
4.2 优化布置方式
4.2.1 间隔层与反射层之比为2∶1
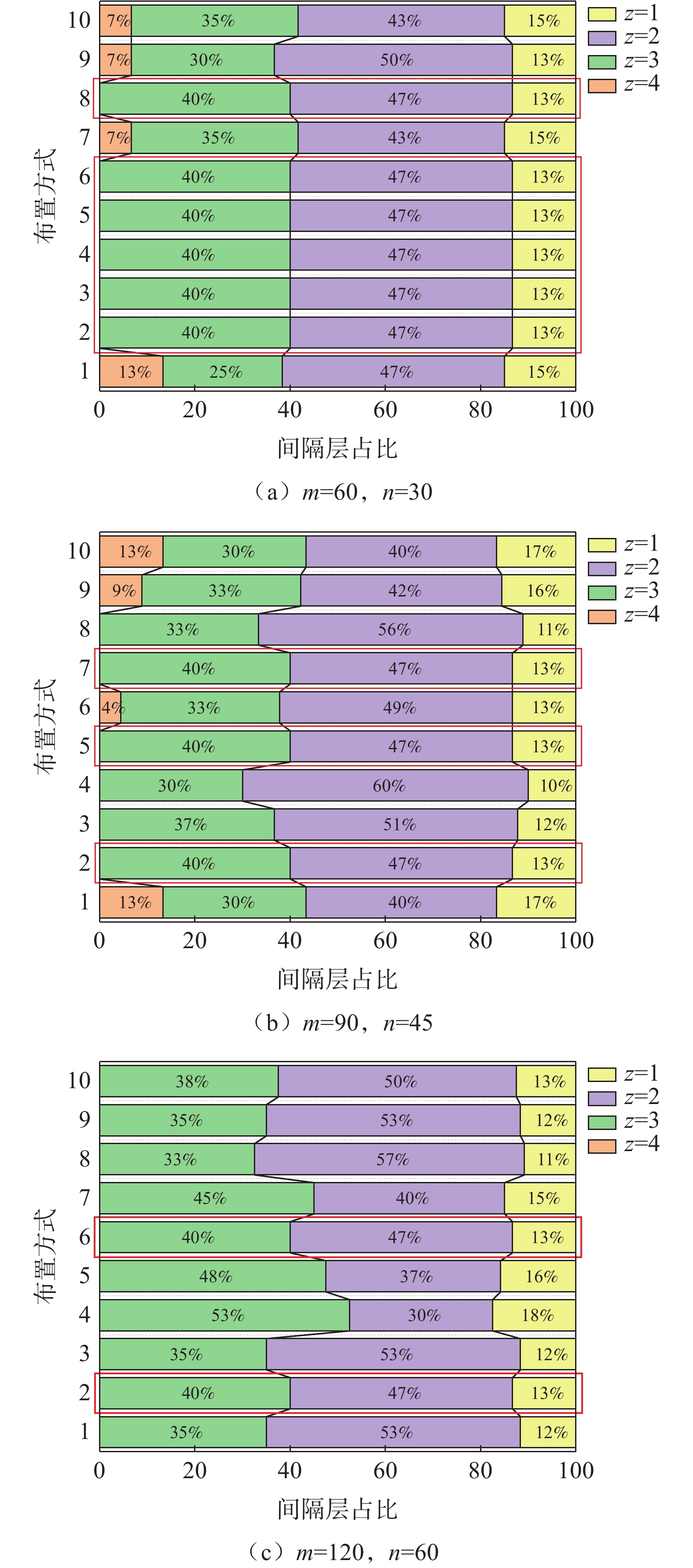
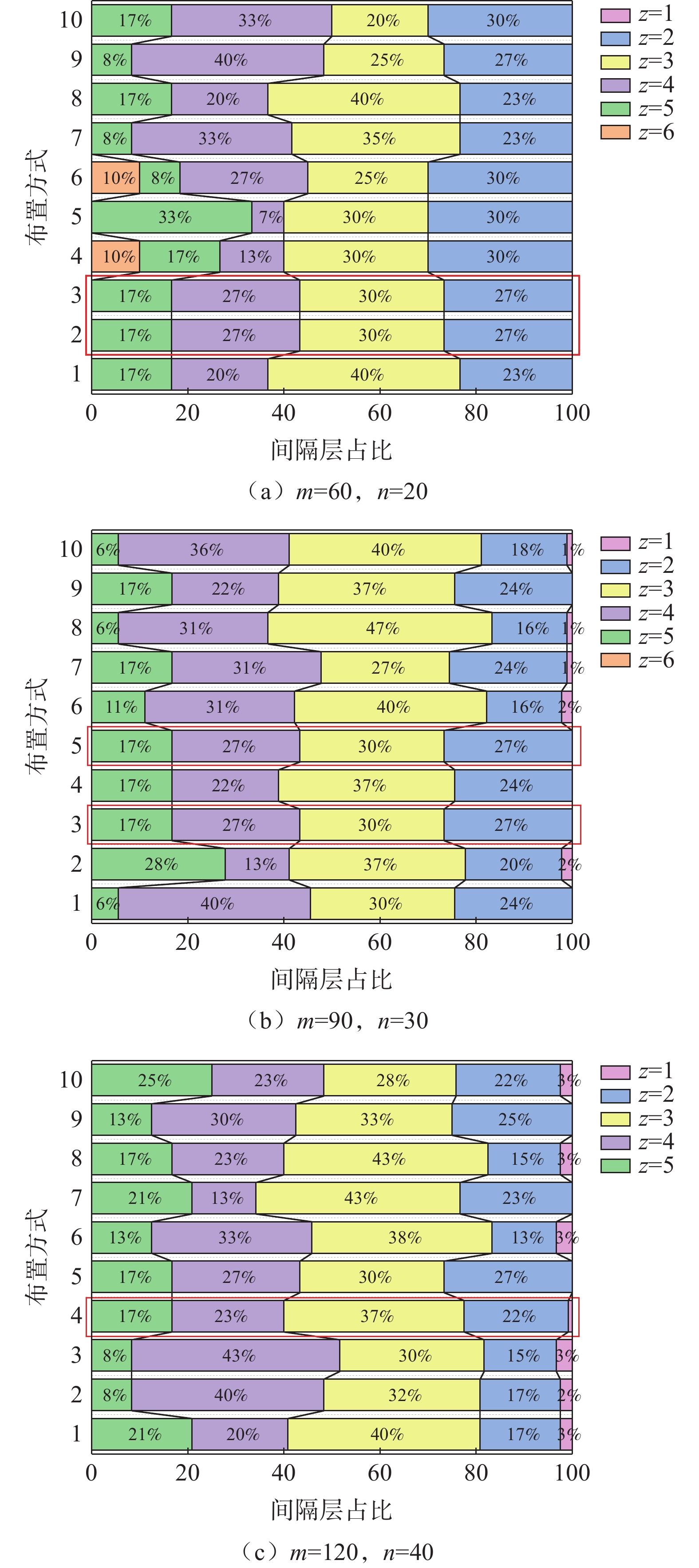
在优化布置求解中，在其他条件相同且间隔层与反射层之比固定为2∶1的情况下，分别对间隔层60层、反射层30层，间隔层90层、反射层45层，间隔层120层、反射层60层三种情况求解优化布置方式。为了便于分析对比，将求解的布置方式按相邻反射层间间隔层数的不同进行归纳，结果如图7所示。
![]()
图 7 通过遗传算法求解的优化布置方式（m∶n=2∶1）Figure 7. Optimal layout method solved by genetic algorithm（m∶n=2∶1）在间隔层与反射层数相同的情况下，虽然通过遗传算法求解的布置方式有所不同，但大致趋势一致。在每两层反射层中布置4层间隔层及3层间隔层的部分（即在z=4及z=3的情况下），间隔层层数总和约为总间隔层数的40%；相邻反射层间布置2层间隔层的部分（z=2），间隔层层数总和约为总间隔层层数的50%；相邻反射层间布置1层间隔层的部分（z=1），间隔层层数总和约为总间隔层层数的10%。此外，虽然在间隔层为60层、90层、120层时，通过遗传算法求解的优化布置方式有所变化，但出现了同一比例分布，即为40%、47%、13%。在间隔层由60层增加至120层的三种情况下，此比例出现的次数逐渐减少。因为当间隔层与反射层层数增加，遗传算法求解的解逐渐不稳定，层数分布方式增多，故而该比例出现的次数减少，说明此比例的分布方式的普遍性，即为相对优化的布置方式。
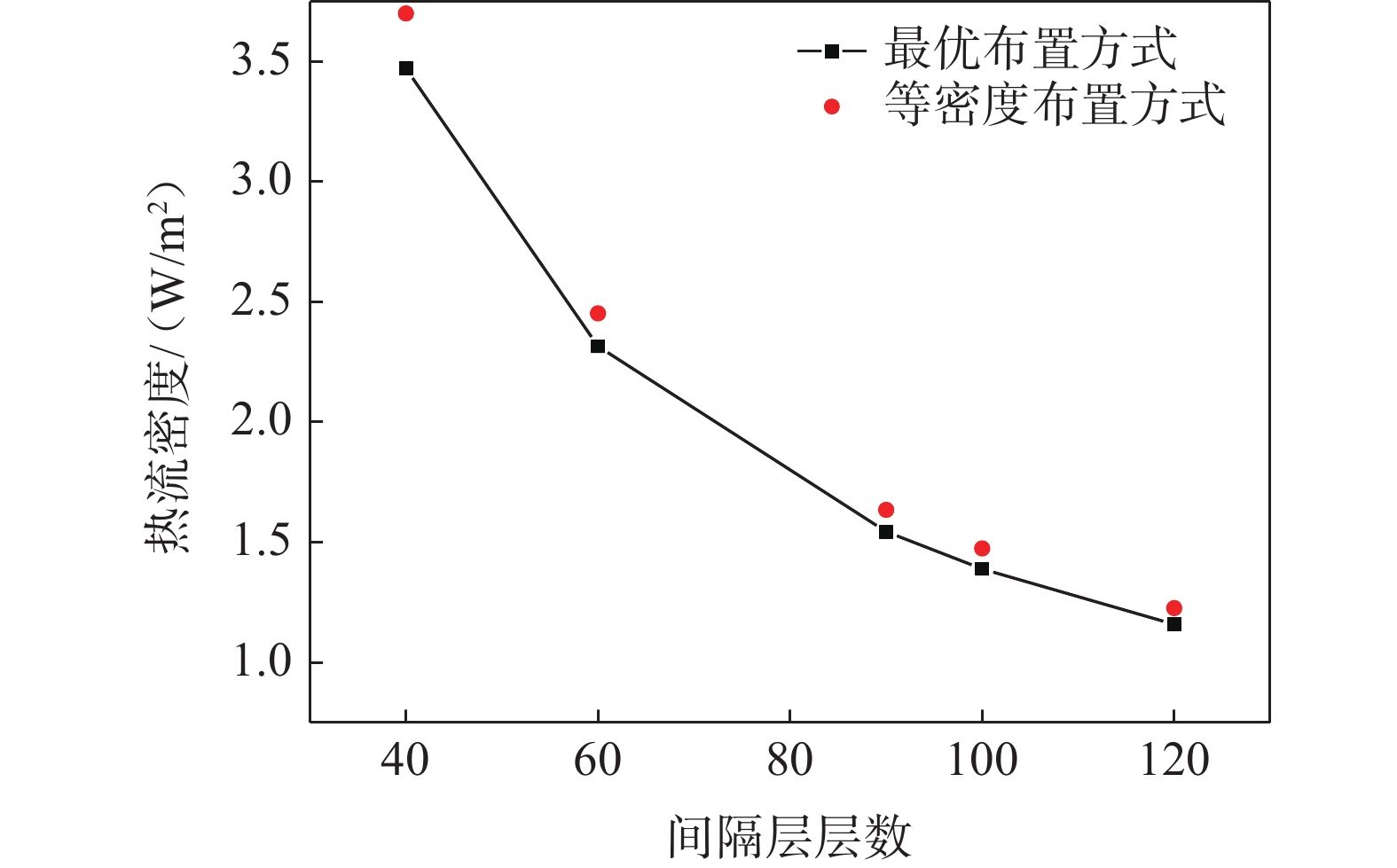
在确保间隔层层数与反射层层数的占比为2∶1，其他条件不变的情况下，求解当间隔层数由40层增加至120层时，以相对优化比例（即为40%∶47%∶13%）布置时的热流密度，结果如图8所示。求解的热流密度几乎始终为均匀层密度布置方式的94%，说明了此比例分布对于在间隔层数与反射层数比例固定2∶1的多层绝热材料布置的扩展性。
4.2.2 间隔层与反射层之比为3:1
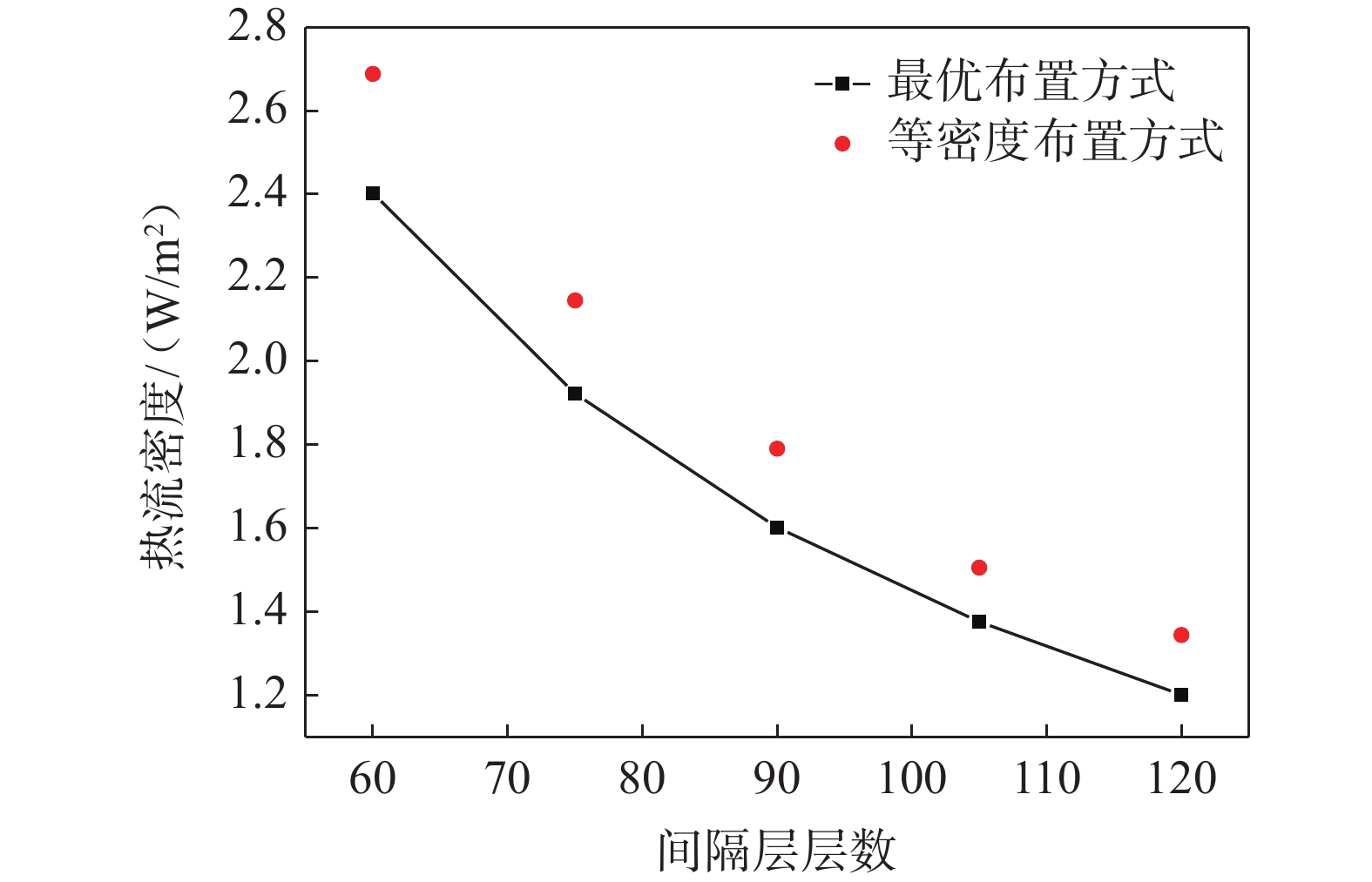
采用间隔层为60层、90层、120层三种情况，控制间隔层与反射层占比为3∶1，其他条件保持不变，通过遗传算法对优化布置方式求解，求解结果如图9所示。虽然各布置方式有所差异，但不同层数间隔层的占比的比例变化不大。在相邻反射层中布置间隔层数大于3的部分（z>3），间隔层层数总和约为总间隔层数的40%；在相邻反射层中布置间隔层数为3的部分（z=3），间隔层层数总和约为总间隔层数的35%；在相邻反射层中布置间隔层数小于3的部分（z<3），间隔层层数总和约为总间隔层数的25%。在图中重复出现了一个特殊的比例即17%、23%、30%、27%。同样在其他条件不变的情况下，按照该比例计算间隔层数由60层增至120层时的热流密度变化，如图10所示。
![]()
图 9 通过遗传算法求解的优化布置方式（m∶n=2∶1）Figure 9. Optimal layout method solved by genetic algorithm（m∶n=2∶1）从图10可见，间隔层为60层时优化布置方式所获得的热流密度为2.40 W/m2，等密度布置方法计算得热流密度2.69 W/m2，采用优化布置方法时的热流几乎始终为采用等密度布置方法热流的89.37%。
5. 结论
通过对多层绝热材料的热模拟分析及实验测试，可以获得如下结论：
（1）通过层与层模型计算了多层绝热材料在实验状况下的热流密度，计算结果与实验测试结果误差小于10%，证明了采用层与层模型对多层绝热材料热流密度进行分析计算的合理性。
（2）基于层与层模型分析了多层绝热材料的热流密度与层密度、热边界温度、总层数等参数之间的关系。多层绝热材料热流密度会随着层密度的降低、总层数的增多而减小；热边界温度会随使用的环境变化而变化，热流密度会随着热边界温度的升高而升高。
（3）在实际使用时应考虑在体积质量及环境因素都不变的情况下降低热流密度。通过遗传算法获得了多层绝热材料的优化布置方案。在间隔层与反射层之比为2∶1的情况下，最具代表的布置方式为随着层位置逐渐靠近热边界，相邻反射层间间隔层数由3层依次递减至1层。其中间隔层数为3层、2层、1层的部分在总间隔层数中的占比分别为40%、47%、13%，相较于等密度多层绝热材料布置方式，热流密度可以降低6%。在间隔层与反射层之比为3∶1的情况下，最具代表的布置方式为随着层位置逐渐靠近热边界，相邻反射层间间隔层数由5层依次递减至2层。其中间隔层数为5层、4层、3层、2层的部分在总间隔层数中的占比分别为17%、23%、30%、27%，相较于等密度多层绝热材料布置方式，热流密度可以降低10.63%。
-
![]()
图 1 层与层模型求解多层绝热材料热流密度计算流程
Figure 1. Calculation process for heat flux of multi-layer insulation materials using layer and layer model
![]()
图 2 多层绝热材料性能实验测试装置
Figure 2. Schematic diagram of experimental testing device for multi-layer insulation material performance
![]()
图 3 三种布置方案在不同层数处的温度分布曲线
Figure 3. Temperature distribution curves of three layout schemes at different levels
![]()
图 4 多层绝热材料层密度变化对热流密度的影响
Figure 4. The effect of density changes in multi-layer insulation materials on heat flux density
![]()
图 5 多层绝热材料热边界温度变化对热流密度的影响
Figure 5. Effect of thermal boundary temperature changes on heat flux density of multilayer insulation material
![]()
图 6 多层绝热材料层数变化对热流密度的影响
Figure 6. The effect of changes in the number of layers of multi-layer insulation materials on heat flux
![]()
图 7 通过遗传算法求解的优化布置方式（m∶n=2∶1）
Figure 7. Optimal layout method solved by genetic algorithm（m∶n=2∶1）
![]()
图 9 通过遗传算法求解的优化布置方式（m∶n=2∶1）
Figure 9. Optimal layout method solved by genetic algorithm（m∶n=2∶1）
表 1 三种多层绝热材料实验及模拟热流密度
Table 1 Experimental and simulated heat flux of three multilayer insulation materials
方案 实验热流密度/（W/m2） 模拟热流密度/（W/m2） 误差/% 1 2.11 1.93 8.49 2 1.64 1.58 3.38 3 1.43 1.41 1.60 
下载: 导出CSV
-
[1] 迟晓婷. 低温推进剂储箱多层绝热结构的传热特性研究 [D]. 哈尔滨:哈尔滨工业大学,2019. [2] 高云飞,王博,王浩任,等. 液氢温区真空多层绝热材料研究进展[J]. 低温工程,2021(6):12−21. [3] 李延娜. 低温贮箱新型组合绝热(SOFI/VD-MLI)传热特性研究 [D]. 兰州:兰州理工大学,2015. [4] ZHENG J,CHEN L,LIU X,et al. Thermodynamic optimization of composite insulation system with cold shield for liquid hydrogen zero-boil-off storage[J]. Renewable Energy,2020,147:824−832. doi: 10.1016/j.renene.2019.09.078
[5] SONG X,XIAO W,WANG P,et al. Hollow glass microspheres-based ultralight non-combustible thermal insulation foam with point-to-point binding structure using solvent evapo-ration method[J]. Construction and Building Materials,2021,292:123415. doi: 10.1016/j.conbuildmat.2021.123415
[6] 李德富,杨炜平,刘小旭. 多层隔热材料传热特性研究现状及展望[J]. 航天器环境工程,2013,30(3):302−309. [7] 李凡杰. 复合多层材料绝热性能研究 [D]. 杭州:浙江大学,2017. [8] 沈铣. 高真空多层绝热材料绝热性能测试系统研究 [D]. 杭州:浙江大学,2013. [9] 王苗,冯军宗,姜勇刚,等. 多层隔热材料的研究进展[J]. 材料导报,2016,30:461−465. [10] 周志雄,魏蔚,汪荣顺. 阻燃型高真空多层绝热材料性能的实验研究[J]. 低温与超导,2006,34(6):428−431. [11] FESMIRE J E,JOHNSON W L. Cylindrical cryogenic calorimeter testing of six types of multilayer insulation systems[J]. Cryogenics,2018,89:58−75. doi: 10.1016/j.cryogenics.2017.11.004
[12] 中华人民共和国国家质量监督检验检疫总局,中国国家标准化管理委员会. 深冷容器用高真空多层绝热材料:GB/T 31480-2015 [S]. 北京:中国标准出版社,2015:24. [13] HEDAYAT A,HASTINGS L J,BROWN T. Analytical modeling of variable density multilayer insulation for cryogenic storage[J]. AIP Conference Proceedings,2002,613(1):1557−1564.
[14] 周佳莹,周炫宇,李晓东. 基于遗传算法的大小交路开行方案优化模型研究[J]. 科技创新与应用,2023,13(31):63−66. -
期刊类型引用(2)
1. 邱一男，康慧芳，马兴龙. 液氢储箱柔性支撑杆设计与仿真分析. 真空与低温. 2025(01): 48-55 . 
本站查看
2. 马晓勇，陈叔平，张亚娟，于洋，于海峰，王波. 间隔层纤维纸微观结构及热物理性质研究. 中国造纸. 2025(03): 60-69 . 百度学术
其他类型引用(1)
计量
- 文章访问数: 30
- HTML全文浏览量: 6
- PDF下载量: 14
- 被引次数: 3
