Design and Test Analysis of Thermometer Calibration Platform for 1.8 K to 300 K
-
摘要:
核聚变装置通常在超低温环境下运行，对温度的精确测量有着严苛的要求。超低温环境下的温度精确测量与标定直接影响着核聚变、高能物理、航空航天等涉及超低温环境的研究领域的发展。根据聚变堆主机系统综合研究设施CRAFT的测试条件，设计了液氦温度计标定平台，可开展1.8~300 K温区内的温度标定与实验研究。该平台通过吉福德-麦克马洪循环制冷机（GM制冷机）以及毛细管节流制冷，实现样品腔降温至1.8 K；通过调节加热器功率控制样品腔温度，可实现1.8~20 K温区内±5 mK波动、20~300 K温区内±15 mK波动的温度环境条件。使用低温测量控制设备对标定区域进行不同温度点位的控温和数据采集，最终得到标定精度结果为：1.8~4.2 K时为±9.54 mK；4.2~20 K时为±22.44 mK；20~300 K时为±346.78 mK。
Abstract:The precise measurement of temperature is crucial for nuclear fusion devices operating in ultra-low temperature magnetic field environments. The accurate temperature measurement and calibration in ultra-low temperature environment has a direct impact on the development of nuclear fusion, high energy physics, aerospace and other research fields involving ultra-low temperature environment. Relying on the comprehensive research facility CRAFT for fusion reactor host systems, a liquid helium temperature calibration platform has been designed to carry out temperature calibration and experimental research in the temperature range of 1.8 K to 300 K. The platform uses the Gifford-McMahon Cycle Chiller （GM Chiller） and capillary throttling refrigeration to cool the sample chamber to 1.8 K. By controlling the temperature of the sample chamber by adjusting the heater power, the temperature environment of ±5 mK fluctuation in the temperature zone of 1.8 K to 20 K and ±15 mK fluctuation in the temperature zone of 20 K to 300 K can be achieved. Low-temperature measurement and control equipment are used for temperature control and data acquisition at different temperature points in the calibration area, resulting in a calibration accuracy of ±4.39 mK at 1.8 K to 4.2 K, ±6.08 mK at 4.2 K to 20 K, and ±75.62 mK at 20 K to 300 K.
-
Keywords:
- thermometer calibration /
- liquid helium /
- cryogenic
-
0. 引言
在计量科学领域中，温度是一个基本的物理量，随着高能物理、超导技术、宇航工程、核能和医学等科学技术领域的快速发展，对超低温环境下的温度测量也随之提出了新的要求[1-3]，如准确度高、复现性能好、使用简便、成本低廉和受磁场影响小等。超低温环境下的温度精确测量与标定直接影响着与之相关的研究领域的发展。温度标定平台为发展极端环境下低温物理参数的精密测量方法与快速响应测试技术，同时为开展低温、真空环境下的低温精密测量测试研究提供了实验测试环境[4]。在此平台上，可以研究与发展1.8 K超流氦下低温温度精密测量方法，开展超低温环境下各种电阻型低温温度计的电阻效应测试研究，并为保障托卡马克聚变装置、高能物理加速器、先进光源等大科学工程实验装置的安全稳定运行提供技术支撑。
近年来，关于温度传感器标定精度的研究有着长足的进步，Nakano等[5]、王博阳等[6]、White等[7]通过对铂电阻计的研究，提高了其在不同温度范围下的标定精度及应用范围；Tew等[8]、Chung等[9]、钱静等[10]改进了低温条件下电阻温度计的插值方法及拟合方程；于颖泽[11]归纳总结了1 K以下超低温环境的获得方法及温度测量技术；Blagg 等[12]和任建平等[13]研究了自热效应对温度计标定结果的影响。这些研究为液氦温区温度传感器的标定提供重要的参考和指导。国内超低温实验研究中广泛应用的温度计是Cernox温度计，其需求量大，标定精度要求高。而对于超低温下尤其是2 K以下的Cernox温度计标定，国内尚未受到充分关注和深入研究。因此，有必要开展对Cernox温度计在超低温环境下的标定精度及其在实际应用中的可行性等方面的深入研究，以满足国内超低温实验环境下对高精度温度测量的需求，其不仅对提高超低温环境下温度测量的准确性具有重要意义，也有望为国内相关领域的科学研究和工程应用提供可靠的技术支持。
1. 温度传感器标定实验装置
1.1 实验样品及标准温度计选用
国内的核聚变装置、高能物理加速器装置、先进光源等大科学工程项目中的大型超导磁体都需要配备大型氦低温系统以进行冷却，整个装置及其低温系统需要精密的低温温度测量，目前低温领域使用最多的是美国LakeShore公司的Cernox温度计。Cernox电阻温度计具有良好的抗磁性、长期稳定性以及可复现性，实验采用的待测及标准温度传感器均为四线接法的CX-SD封装Cernox-1050温度计，表1给出标准Cernox CX1050温度传感器在不同温度下的扩展不确定度及长期稳定性。
表 1 Cernox CX1050温度传感器在不同温度下的精度Table 1. Accuracy of the Cernox CX1050 temperature sensor at different temperatures温度/K 扩散不确定度/mK 长期稳定性/mK 1.4 ±5 ±3 4.2 ±5 ±3 10 ±6 ±6 20 ±9 ±12 77 ±16 ±46 300 ±40 ±180 1.2 液氦温度传感器标定系统
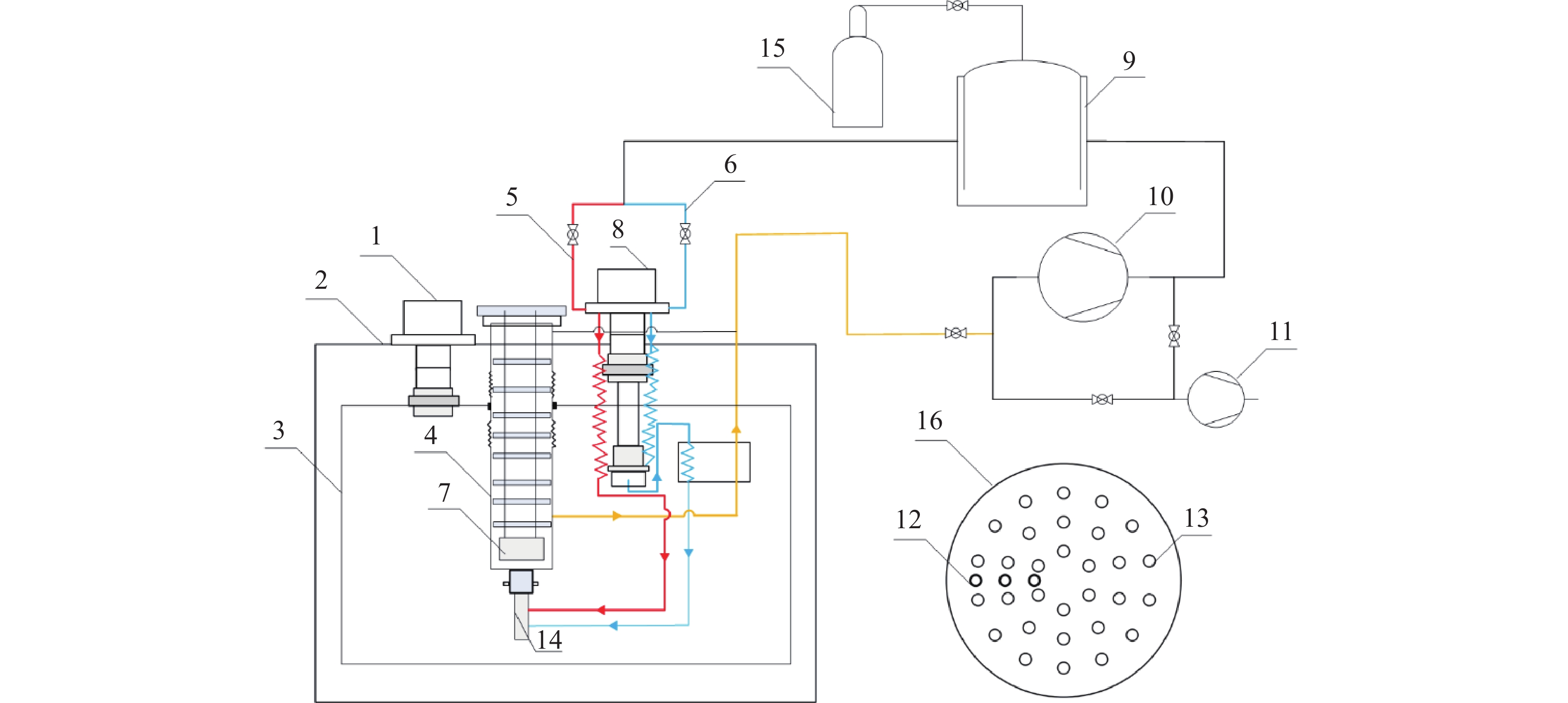
标定系统主要由真空系统、低温恒温系统、温度传感器样品腔及低温测量控制设备构成。真空腔组件由提供负压的真空机组组成；低温恒温系统由两台GM制冷机组成，GM制冷机1用于降温冷屏，GM制冷机2用于为氦循环提供冷量；低温测量控制设备配置低温温度传感器、压力变送器等测量仪表，以及温控仪、采集控制设备等。
传感器标定系统在液氦温区可以实现真空腔10−5 Pa的压力，在1.8~20 K时使用低温进气管路，通过调节流量和控温加热器功率可以达到10 min内±5 mK的温度稳定性，在20~300 K时使用高温进气管路，通过控制控温加热器功率使温度稳定性优于10 min内±15 mK，取值频率为2次/s。
如图1所示，系统运行前的流程为：连接真空泵对真空腔进行抽气，直至常温下压力降至0.5 Pa后，关闭真空腔阀门以维持真空度；然后将样品腔抽口与真空泵连接，开启氦循环管路的所有阀门，并开启循环泵和分子泵，将氦循环管路抽气至常温下0.1 Pa，随后补入氦气并再次抽真空至0.1 Pa，关闭分子泵及其与循环泵之间的连接阀门。真空腔抽气及样品腔置流换洗完成后开始氦循环降温流程：开启两台GM制冷机，关闭低温氦气进气管路的阀门，通过氦气瓶向缓冲罐输入氦气，这时在循环泵的作用下，缓冲罐内的氦气会走高温氦气进气管路经过制冷机的冷头，将冷头的冷量带入样品腔，然后氦气通过循环泵回到缓冲罐；待样品架的温度降到20 K后，关闭高温氦气进气管路的阀门，开启低温氦气进气管路的阀门，低温氦气进气管路的孔径较小，且在二级冷头处设置毛细管段，通过毛细管段的节流作用将冷量带入样品腔，最后使样品架的温度达到1.8 K。另外，制冷机1的一级冷头连接冷屏，使冷屏温度降至50 K。
![]()
图 1 温度传感器标定平台流程及样品架孔位示意图1. GM制冷机1；2. 真空腔；3. 冷屏；4. 温度传感器样品腔；5. 高温氦气进气管路；6. 低温氦气进气管路；7. 温度传感器样品架；8. GM制冷机2；9. 氦气缓冲罐；10. 循环泵；11. 分子泵；12. 标准温度传感器孔位；13. 待测温度传感器孔位；14. 控温加热器；15. 氦气瓶；16. 样品架。Figure 1. Temperature sensor calibration platform flow and sample frame hole position diagram测试样品腔组件主要由样品杆和温度传感器样品架组成，为传感器样品的标定提供独立的氦循环通路。温度传感器样品架可以同时安装30个待测温度传感器以及3个标准温度传感器。温度传感器通过电流引线连接低温测量控制设备。样品架由无氧铜制作，通过拉杆吊装在样品腔底部，其上有辐射挡板。样品架在1.8~4.2 K时热扩散系数高达0.15 m2/s[14]，同时标准温度传感器和待测温度传感器安装位置半径相同，由于样品架有超高的导热率及其形状为薄圆盘，温度梯度近似为径向分布，标准温度传感器和待测温度传感器可视作等温。
低温测量控制设备配有一台Lakedhore 公司出品的Model 336控温仪及四台Model 224测温仪。使用研华IPC610MB-JQ工控机以及西门子PLC控制器控制加热器功率，以达到稳定控温的目的。
1.3 标定实验系统热力学计算
标定系统的热力学计算涉及漏热计算、真空泵选型以及制冷机功率计算。热力学计算可以确保系统能够达到所需的工况，并在工作时保持稳定运行。这些计算对于系统的设计和优化非常关键，能够提高系统的性能和可靠性。
制冷机1冷头在50 K的热负荷主要包含冷屏辐射漏热、残余气体分子间的对流换热以及固体传导漏热等，经计算，总漏热为21.6 W。选择一台万瑞GM415制冷机可满足使用要求。
制冷机2通过一级、二级冷头将氦气降温至4.2 K，经计算得出其热负荷如表2所列。制冷机2选取住友GM415制冷机，一级冷头冷量为35 W@50 K，二级冷头冷量为1.5 W@4.2 K，满足制冷需求。
表 2 真空泵抽速及制冷机2热负荷计算Table 2. Calculation of vacuum pump flowrate and chiller 2 thermal load设备 参数 值 真空泵 质量流量/（g/s） 0.02 真空泵抽速/（L/min） 540 制冷机2 一级冷头热负荷/W 25.97 二级冷头热负荷/W 1.11 基于热力学计算结果，温度标定平台真空泵选取大阪真空NeoDry60E 小型空冷干式真空泵，最高抽速可达
1000 L/min，满足抽速需求。2. 标定实验
2.1 标定系统实验流程
为实现液氦温区的标定，需要对系统进行抽气以尽可能减小外界的热辐射，连接外部真空泵对真空腔抽气，使其能在液氦温区达到10−5 Pa的压力，并使用循环泵和分子泵串联对样品腔进行置流换洗，保证循环过程中氦冷却介质的纯度，防止管路堵塞。
使用高温氦气进气管路进行大流量氦气循环，将制冷机的冷量带到循环管路的各部分以实现快速预冷。温度降至20 K后，关闭高温氦气进气管路阀门，打开低温氦气进气管路阀门，通过毛细管节流作用实现1.8 K低温。标定实验开始前，一般已保持超过5 h的最低温恒温时间，可以保障系统温度均匀性。
通过Lakeshore公司提供的测温点位进行控温，在1.8~20 K区间，使用低温氦气进气管路，保持升温速率小于20 mK/min，控温稳定时间大于10 min。为了降低样品架温度传导过程中的误差，选取数据时排除稳定阶段前5 min的数据。在20~300 K区间，切换为高温氦气进气管路，保持升温速率小于50 mK/min，控温稳定时间大于20 min。同样为了降低样品架温度传导过程中的误差，选取数据时排除稳定阶段前15 min的数据。
2.2 标定实验数据处理
实验数据的拟合处理会直接影响到传感器标定精度，一般将拟合过程的不确定度记为A类不确定度。一般负温度系数校准拟合会采用切比雪夫多项式做最小二乘法拟合[15]，拟合式如下：
$$ T = \frac{{{a_0}}}{2} + \sum\nolimits_{i = 1}^n {{a_i}\cos [i} \arccos (A\ln R + B)] $$ (1) $$ A = \frac{2}{{\ln {R_{\max }} - \ln {R_{\min }}}} $$ (2) $$ B = 1 - \frac{{2\ln {R_{\max }}}}{{\ln {R_{\max }} - \ln {R_{\min }}}} $$ (3) 式中：T为温度；R为传感器电阻；ai为拟合系数；A、B为归一化常数； Rmax和Rmin分别为电阻值的最大最小值。拟合标准差按式（4）计算：
$$ {D_{{\text{T,std}}}} = \sqrt {\sum\nolimits_{{{j}} = 1}^m {\frac{{{{({T_{{\text{C}}{{j}}}} - {T_{{\text{E}j}}})}^2}}}{{m - n - 1}}} } $$ (4) 式中：DT，std为校准数据拟合的标准偏差；TCj为校准点数据拟合后得出的温度值；TEj为校准点实测的温度值；m为参加拟合的校准点数；n 为拟合的方次。
使用Matlab软件对数据进行拟合。由于国内大型低温超导设备要求的温度一般在4.2 K以下，需将1.8~300 K的实验数据以4.2 K为节点分段处理，同时由于标定实验在20 K时需要切换管路，因此将数据分为4.2~20 K和20~300 K两段。
3. 标定实验结果及分析
3.1 标定实验结果
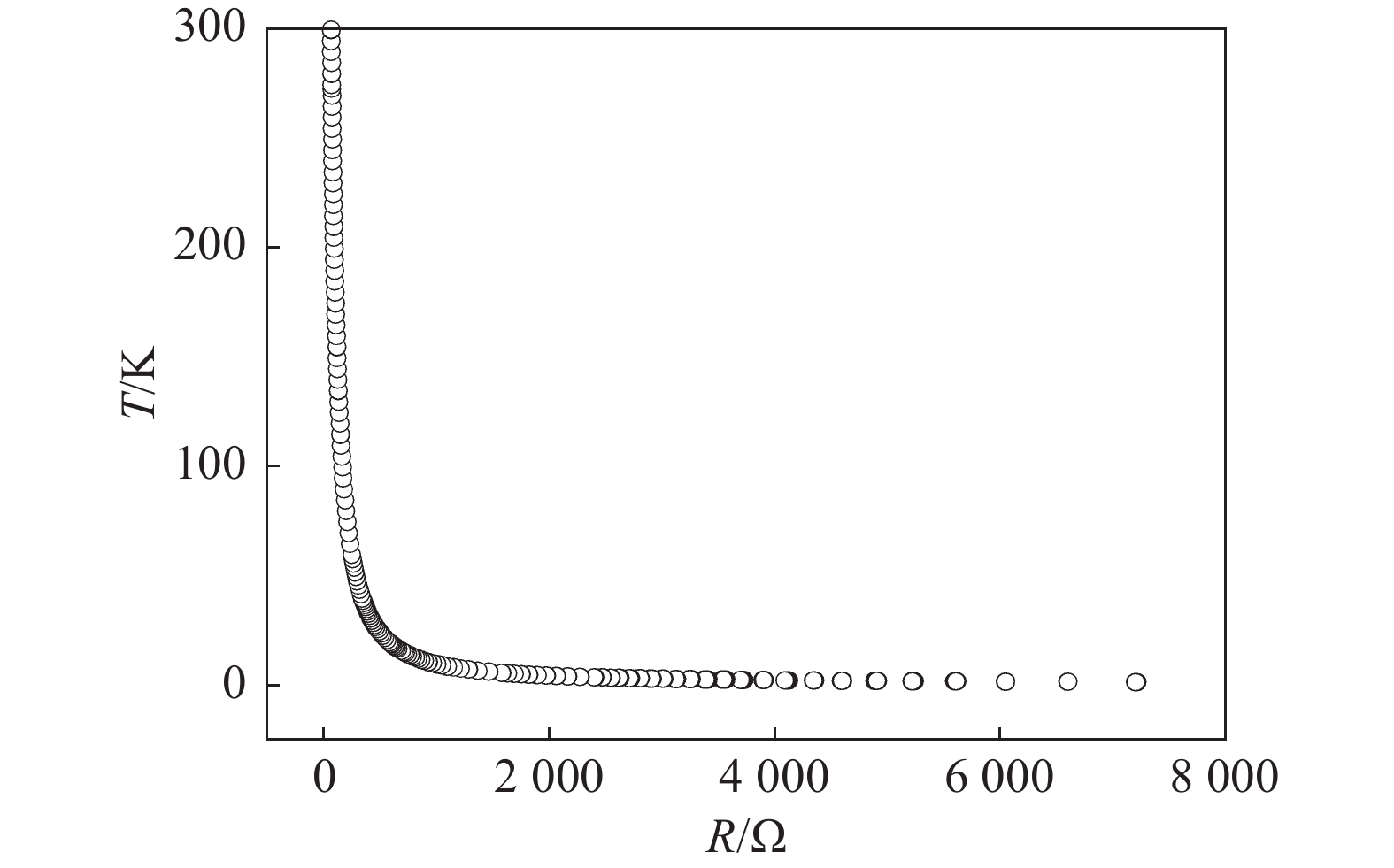
图2为待标定传感器的处理后（1.8~300 K）的R-T曲线。表3为不同温区内温度点的取值间隔。
表 3 不同温度区间内的温度点取值间隔Table 3. The interval between temperature points in different temperature ranges温度/K 间隔温度/K 1.8 ~ 4 0.1 4 ~ 6 0.2 6 ~ 20 0.5 20 ~ 40 1.0 40 ~ 50 2.0 50 ~ 75 5.0 77.35 — 80 ~300 5.0 将数据分三段导入Matlab软件进行分析处理，选用Levenberg-Marquardt算法，选取一支温度传感器标定数据，处理结果如表4所列，公式拟合结果如表5所列。
表 4 标定实验拟合结果Table 4. The fitting results of the calibration experiment温区/K 公式方次 拟合标准差/mK 1.8 ~ 4.2 4 0.3 4.2 ~ 20 4 1.8 20 ~ 300 7 0.8 表 5 公式系数Table 5. Formula coefficient系数 1.8 ~ 4.2 K 4.2~20 K 20~300 K a0 5.4759 20.4325 238.9549 a1 − 1.0852 − 7.5862 − 131.8734 a2 0.1641 1.8551 38.9273 a3 − 0.0210 − 0.3203 − 7.6418 a4 0.0025 0.0340 1.4353 a5 — — − 0.4577 a6 — — 0.1668 a7 — — − 0.0297 A 1.8137 1.2525 0.9021 B − 15.1094 − 9.5564 − 4.7385 3.2 标定结果不确定度分析
温度传感器标定的不确定性一般分A、B两类，A类不确定度即式（4）得出的拟合方程标准差。在3.1节已给出。
B类标准差由温度计偏差、电测设备偏差、控温温度性偏差等引入，讨论如下。
（1）标准温度计引入的不确定度
由标准温度计引入的不确定度按式（5）计算：
$$ {u_1} = \frac{{{U_{\text{C}}}}}{{{k_1}}} $$ (5) 式中：UC为标准温度计的扩展不确定度；k1为置信因子，取2。
由Cernox-1050说明书可知，在1.8~4.2 K时，标准温度计扩展不确定度小于±5 mK；4.2~20 K时，小于±9 mK；在20~300 K时，小于±40 mK。
计算可得三个温区引入的不确定度分别为2.5 mK、4.5 mK、20 mK。
（2）标准温度计电测设备引入的不确定度
该不确定按式（6）计算。
$$ u_2=\Delta\frac{\mathrm{d\mathit{T}/d\mathit{R}}}{k_2} $$ (6) 式中：k2为置信因子，取$\sqrt 3 $；dT/dR为温度随电阻的变化率；$\Delta $为电测设备的精度。
标定系统测试电阻Model 224在三个温度范围内的测量精度分别为±1 Ω显示读数的0.04% 、±0.1 Ω显示读数的0.04% 和±0.1 Ω显示读数的0.04% 。将标准温度传感器附带的温度曲线数据分别代入式（6）。计算结果如表6所列。
表 6 标准温度计电测设备引入的不确定度计算表Table 6. Uncertainty introduced by standard thermometers electrical measuring equipment温区/K 电阻/Ω dT/dR u2/mK 1.8~4.2 3507 − 0.00054 0.469 4.2~20 393 − 0.00778 1.155 20~300 59 − 5.78035 112.133 （3）待测温度计电测设备引入的不确定度
待测温度计电测设备引入的不确定度u3计算方式和标准温度计u2相同，使用同样的方法计算校准实验中的数据，表7为1.8~300 K内待测温度计电测设备引入的不确定度最大时的电阻以及dT/dR。
表 7 待测温度计电测设备引入的不确定度计算表Table 7. Uncertainty caused by the electrical measuring device of the thermometer to be measured温区/K 电阻/Ω dT/dR u3/mK 1.8~4.2 3000 − 0.00098 0.749 4.2~20 579 − 0.03321 6.364 20~300 63 − 5.8722 119.481 （4）标准温度计长期不确定度
长期不确定度按式（7）计算。
$$ {u_4} = \frac{{{U_{\text{L}}}}}{{{k_4}}} $$ (7) 式中：UL为标准温度计长期稳定性的值；k4为置信因子，取$\sqrt 3 $。
Cernox 1050传感器在4.2 K时长期稳定性为3 mK，20 K时为12 mK，300 K时为180 mK。计算可知，由温度计长期稳定性引入的不确定度分别为1.732 mK、6.928 mK和51.962 mK。
（5）控温波动引入的不确定度
该不确定按式（8）计算。
$$ {u_5} = \frac{{\Delta {T_5}}}{{{k_5}}} $$ (8) 式中：k5为置信因子，取$\sqrt 2 $；$\Delta {T_5}$为温度波动范围。
1.8~20 K时，温度最大波动小于5 mK，20~300 K时，小于15 mK。计算得出由控温波动引入的不确定度分别为3.55 mK、3.55 mK和10.6 mK。
（6）其他因素的影响
温度传感器标定时，自热效应和铜块热偏差也是误差的重要来源，根据相关研究，1.8~20 K区间内，励磁电流小于30 μA时，自热效应忽略不计。20 ~300 K区间内，最小电阻为63 Ω，励磁电流最大为100 μA，自热效应造成的误差为15.56 μK[16]，可以忽略。铜块热偏差由设计保证可以忽略不计。
综合A类和B类各种不确定度，表8列出了各种标定不确定度的计算结果。
表 8 标定不确定度分类明细表Table 8. Calibration uncertainty calculation results序号 不确定度来源 1.8~4.2 K 4.2~20 K 20~300 K 1 拟合标准差/mK 0.3 1.8 0.8 2 标准温度计/mK 2.5 4.5 20 3 标准温度计电测设备/mK 0.469 1.155 112.133 4 待测温度计电测设备/mK 0.749 6.364 119.481 5 长期稳定性 1.732 6.928 51.962 6 控温波动/mK 3.55 3.55 10.6 7 自热效应/mK 0 0 0 8 样品架温差/mK 0 0 0 根据不确定度的方根合成计算方法，计算出标定实验的测量标准不确定度：
$$ U = ku = k\sqrt {{D_{{\text{T,std}}}}^{\text{2}} + \sum\nolimits_{k = 1}^p {u_{{k}}^2} } $$ (9) 式中：U为扩展不确定度；u为合成标准不确定度；k为置信因子，取2；p为不确定度来源项目数；uk为各项不确定度。
经计算，合成标准不确定度分别为：在1.8~4.2 K时，±4.77 mK；4.2~20 K时，±11.22 mK；20~300 K时，±173.39 mK。
扩展不确定度分别为：在1.8~4.2 K时，±9.54 mK；4.2~20 K时，±22.44 mK ；20~300 K时，±346.78 mK。
4. 结论
超流氦温区温度标定平台实现了液氦温区温度传感器的自主标定。标定平台在1.8~4.2 K时，扩展不确定度U1=±9.54 mK；在4.2 ~20 K，扩展不确定度U2=±22.44 mK ；在20 ~300 K时，扩展不确定度U3=±346.78 mK。
该平台可以满足聚变堆配套的超导磁体系统在运行时的测温需求，以及国内大部分大科学实验装置在超低温条件下的温度测量要求。在此平台上，能够研究与发展1.8 K超流氦下低温温度精密测量方法，开展各种电阻型低温温度计的测试研究，以此为保障托卡马克聚变装置、高能物理加速器、先进光源等大科学工程实验装置的安全稳定运行提供技术支撑。
-
![]()
图 1 温度传感器标定平台流程及样品架孔位示意图
1. GM制冷机1；2. 真空腔；3. 冷屏；4. 温度传感器样品腔；5. 高温氦气进气管路；6. 低温氦气进气管路；7. 温度传感器样品架；8. GM制冷机2；9. 氦气缓冲罐；10. 循环泵；11. 分子泵；12. 标准温度传感器孔位；13. 待测温度传感器孔位；14. 控温加热器；15. 氦气瓶；16. 样品架。
Figure 1. Temperature sensor calibration platform flow and sample frame hole position diagram
表 1 Cernox CX1050温度传感器在不同温度下的精度
Table 1 Accuracy of the Cernox CX1050 temperature sensor at different temperatures
温度/K 扩散不确定度/mK 长期稳定性/mK 1.4 ±5 ±3 4.2 ±5 ±3 10 ±6 ±6 20 ±9 ±12 77 ±16 ±46 300 ±40 ±180 
下载: 导出CSV
表 2 真空泵抽速及制冷机2热负荷计算
Table 2 Calculation of vacuum pump flowrate and chiller 2 thermal load
设备 参数 值 真空泵 质量流量/（g/s） 0.02 真空泵抽速/（L/min） 540 制冷机2 一级冷头热负荷/W 25.97 二级冷头热负荷/W 1.11
下载: 导出CSV
表 3 不同温度区间内的温度点取值间隔
Table 3 The interval between temperature points in different temperature ranges
温度/K 间隔温度/K 1.8 ~ 4 0.1 4 ~ 6 0.2 6 ~ 20 0.5 20 ~ 40 1.0 40 ~ 50 2.0 50 ~ 75 5.0 77.35 — 80 ~300 5.0
下载: 导出CSV
表 4 标定实验拟合结果
Table 4 The fitting results of the calibration experiment
温区/K 公式方次 拟合标准差/mK 1.8 ~ 4.2 4 0.3 4.2 ~ 20 4 1.8 20 ~ 300 7 0.8
下载: 导出CSV
表 5 公式系数
Table 5 Formula coefficient
系数 1.8 ~ 4.2 K 4.2~20 K 20~300 K a0 5.4759 20.4325 238.9549 a1 − 1.0852 − 7.5862 − 131.8734 a2 0.1641 1.8551 38.9273 a3 − 0.0210 − 0.3203 − 7.6418 a4 0.0025 0.0340 1.4353 a5 — — − 0.4577 a6 — — 0.1668 a7 — — − 0.0297 A 1.8137 1.2525 0.9021 B − 15.1094 − 9.5564 − 4.7385
下载: 导出CSV
表 6 标准温度计电测设备引入的不确定度计算表
Table 6 Uncertainty introduced by standard thermometers electrical measuring equipment
温区/K 电阻/Ω dT/dR u2/mK 1.8~4.2 3507 − 0.00054 0.469 4.2~20 393 − 0.00778 1.155 20~300 59 − 5.78035 112.133
下载: 导出CSV
表 7 待测温度计电测设备引入的不确定度计算表
Table 7 Uncertainty caused by the electrical measuring device of the thermometer to be measured
温区/K 电阻/Ω dT/dR u3/mK 1.8~4.2 3000 − 0.00098 0.749 4.2~20 579 − 0.03321 6.364 20~300 63 − 5.8722 119.481
下载: 导出CSV
表 8 标定不确定度分类明细表
Table 8 Calibration uncertainty calculation results
序号 不确定度来源 1.8~4.2 K 4.2~20 K 20~300 K 1 拟合标准差/mK 0.3 1.8 0.8 2 标准温度计/mK 2.5 4.5 20 3 标准温度计电测设备/mK 0.469 1.155 112.133 4 待测温度计电测设备/mK 0.749 6.364 119.481 5 长期稳定性 1.732 6.928 51.962 6 控温波动/mK 3.55 3.55 10.6 7 自热效应/mK 0 0 0 8 样品架温差/mK 0 0 0
下载: 导出CSV
-
[1] MANZAGOL J,ATTARD A,LUCHIER N,et al. Thermometric chains for ITER superconductive magnets[J]. Fusion Engineering and Design,2019,146:651−655. doi: 10.1016/j.fusengdes.2019.01.047
[2] COURTS S S. A standardized diode cryogenic temperature sensor for aerospace applications[J]. Cryogenics,2016,74:172−179. doi: 10.1016/j.cryogenics.2015.09.006
[3] 白波,胡海韬,袁宝,等. 中国散裂中子源4 K低温恒温器研制及测试[J]. 低温与超导,2023,51(7):1−6. [4] XUE R,YANG S Q,XIE X J,et al. Influence of key parameters on the performance of a helium cryogenic system in refrgeration and liquefaction modes[J]. Cryogenics,2021,121:103386.
[5] NAKANO T,KAWAMURA Y,IMAMURA T,et al. ITS-90 non-uniqueness and evaluation of characteristics of new 1 000 Ω type platinum resistance thermometers for low-temperature measurement[J]. Measurement Science and Technology,2020,31(9):094017. doi: 10.1088/1361-6501/ab8089
[6] 王博阳,曾凡超,黄安贻,等. PPRTs偏差方程外推至-189.344 2~156.598 5 ℃温区的研究[J]. 计量学报,2022,43(7):869−876. doi: 10.3969/j.issn.1000-1158.2022.07.06 [7] WHITE D R,ROURKE P M C. Standard platinum resistance thermometer interpolations in a revised temperature scale[J]. Metrologia,2020,57(3):035003. doi: 10.1088/1681-7575/ab6b3c
[8] TEW W L,RUSBY R L,LIN P,et al. A Standardized interpolation of temperature using rhodium–iron resistance thermometers over the interval 4.2 K to 24.5 K[J]. International Journal of Thermophysics,2015,36(8):2036−2059. doi: 10.1007/s10765-015-1877-4
[9] CHUNG J P,OH S W. A residual compensation method for the calibration equation of negative temperature coefficient thermistors[J]. Thermochimica Acta,2015,616:27−32. doi: 10.1016/j.tca.2015.07.015
[10] 钱静,翁佩德,罗家融,等. 温度计标定中曲线拟合的应用及研究[J]. 低温与超导,2009,37(11):26−28. [11] 于颖泽. 1 K以下超低温的获得与测量方法[J]. 低碳世界,2017(29):262−263. doi: 10.3969/j.issn.2095-2066.2017.29.167 [12] BLAGG K,CASTAGNEDE A,SINGH M. On-chip heating effects in electronic measurements at cryogenic temperatures[J]. Cryogenics,2022,126:103536. doi: 10.1016/j.cryogenics.2022.103536
[13] 任建平,孙建平,李婷,等. 标准铂电阻温度计自热效应对测量结果的影响[J]. 计量学报,2021,42(5):589−594. [14] 吴萌,方志春,王春栋,等. 基于PPMS测试系统的低温温度计标定研究[J]. 低温工程,2022(6):13−17. [15] 林鹏. 负温度系数低温电阻温度计校准规范:JJF 1170-2007[S]. 北京:国家质量监督检验检疫总局,2007. [16] 王珞畅,刘磊,周文杰,等. CERNOX温度计自热效应[J]. 低温与超导,2020,48(3):17−21.
计量
- 文章访问数: 38
- HTML全文浏览量: 7
- PDF下载量: 23
