Optimization Design and Numerical Simulation of High-power MPCVD Resonance Cavity
-
摘要:
微波等离子体化学气相沉积（MPCVD）装置能够非常高效地产出高质量的金刚石薄膜，由于波长和腔体结构的限制，传统2.45 GHz MPCVD装置所沉积出的薄膜面积直径通常维持在50～70 mm之间。以增大金刚石膜沉积面积为目标，通过对微波电场进行仿真分析，优化设计腔体尺寸，并对电子密度和温度的分布特性进行数值模拟，以保证等离子体能够均匀分布于沉积片上，将沉积直径扩增至90 mm。模拟结果表明，当腔内微波源功率为
6000 W，压力为14.7 kPa时，沉积片上可以产生电子密度和温度分别为1.76×1018 m−3和4.7×104 K的高密度且均匀的等离子体。Abstract:The Microwave Plasma Chemical Vapor Deposition（MPCVD） system has emerged as a highly efficient method for producing high-quality diamond films, which have a wide range of applications in electronics, optics, and cutting tools. However, traditional MPCVD systems operating at a frequency of 2.45 GHz face inherent limitations regarding the diameter of the film area that can be deposited. Typically, this diameter ranges from 50 to 70 mm, constraining the potential for large-area applications. To address this challenge, recent efforts have focused on optimizing the design of the cavity dimensions within the MPCVD system. By simulating and analyzing the microwave electric field, researchers have been able to identify configurations that enhance the deposition area for diamond films. These optimizations are critical for increasing the uniformity and quality of the deposited films, allowing for more versatile industrial applications. In addition to cavity design improvements, numerical simulations have been conducted to investigate the distribution characteristics of electron density and temperature within the plasma. Achieving a uniform plasma distribution on the deposition substrate is vital for enhancing the overall film quality and expanding the deposition diameter. Through these simulations, researchers have successfully demonstrated that the deposition diameter can be increased to 90 mm, significantly surpassing the limitations of traditional systems. The simulation results reveal that when the microwave source power is set to 6 000 W and the pressure within the cavity is maintained at 14.7 kPa, a high-density and uniform plasma is generated on the deposition substrate. Specifically, the electron density reaches an impressive value of 1.76×1018 m−3, while the temperature of the plasma is approximately 4.7×104 K. These findings indicate that the optimized MPCVD system can produce high-quality diamond films over a larger area, paving the way for advancements in various technological fields. The enhancements achieved through careful simulation and design highlight the potential for further developments in plasma deposition techniques.
-
Keywords:
- microwave plasma /
- MPCVD /
- diamond film /
- numerical simulation
-
0. 引言
金刚石薄膜作为一种具有极高硬度、高耐磨性和优异导热性的材料，已经成为现代科技中不可或缺的一部分。制备金刚石薄膜的方法包括热丝沉积法（HF-CVD）[1]、直流等离子体喷射法（DC-arcjet）[2]、直流等离子体沉积法（DC-plasma）[3]和微波等离子体化学气相沉积法（MPCVD）[4]等。
近年来，通过化学气相沉积（Chemical Vapor Deposition，CVD）技术制备金刚石薄膜已经成为一种备受关注的方法。但是，金刚石薄膜的质量通常受到制备条件的限制。为了制备高品质的金刚石薄膜，需要进一步研究和探索制备工艺，如气体组成、反应条件等，以提高薄膜的结晶度、纯度和致密性等性能。微波等离子体化学气相沉积（MPCVD）是合成高质量金刚石薄膜最广泛使用的技术[5-7]，具有成本低、制备过程简单等优点，能够在较低温度和压力下实现金刚石薄膜的制备，同时还具备良好的可控性和高稳定性。MPCVD谐振腔利用微波能量激发等离子体，使其在化学气相沉积过程中产生化学反应，从而在基板表面沉积出所需的薄膜材料。与传统的化学气相沉积技术相比，微波等离子体化学气相沉积技术具有较高的沉积速率、较低的沉积温度和较好的薄膜质量控制等优点，因此在半导体器件、光电子器件、涂层材料等领域得到广泛应用。
MPCVD谐振腔的数值模拟常用的气体模型是H2与甲烷（CH4）的混合模型，且CH4占比小。根据现有文献[8-10]，在固定的功率和压力输入下，CH4的存在与否对所形成的电子密度等参数都影响甚微。本文将在纯氢气环境下进行数值模拟，设计一款2.45 GHz频率下以TM021谐振模式为工作模式的MPCVD谐振腔，在谐振腔中引入H2，并利用由微波发生器产生的微波能量来激活等离子体，通过频域分析和数值模拟的方法来研究纯氢等离子体在不同环境下等离子体域内性质的变化（包括电场分布、电子密度和气体温度等）。
1. MPCVD谐振腔的模拟理论
微波谐振现象即微波场中的某些元件（如空心腔、波导等）的尺寸满足特定条件时，会出现共振现象，在一定频率下电磁场能量在系统中不断反射并形成驻波，从而达到能量集中和传输的目的。谐振频率是指在谐振条件下微波系统的工作频率，谐振模式则描述了谐振器中电磁场的分布形态和特性，常见的谐振模式有横磁（TM）、横电（TE）和横电磁（TEM）模式等，TM模式中磁场与波传播方向垂直而电场与波传播方向平行，TE模式中电场与波传播方向垂直而磁场与波传播方向平行，而TEM模式中电场和磁场均与波的传播方向垂直。
微波谐振理论在通信、雷达、天线、微波加热等领域都有广泛的应用，例如，微波天线中的谐振可以用来调节频率和增强信号传输效果。现如今微波放电最常使用的频率为2.45 GHz和915 MHz，微波能量被微波源转换成气体分子内能，以便激发并电离气体分子，形成等离子体。不同于直流放电和射频放电，微波放电是一种利用高频电磁波电离工作气体，从而生成等离子体的技术。微波在传播时可以穿透等离子体，这种技术不需要内部电极，能够有效防止电极高温分解所产生的污染。在微波放电反应室中，气体分子的核外电子受到微波能量的影响而获得动能并加速运动，这些电子在与其他分子碰撞时会产生能量交换、损失和电离解离，进而产生自由电子和正离子。同时，运动的电子和离子激发电磁场并与外界电磁场相互作用，致使等离子体电离参数发生改变。
1.1 电磁场模块的计算
通过式（1）的Maxwell方程可以计算MPCVD谐振腔中的微波电场：
$$ \nabla\mu_{\mathrm{r}}^{-1}(\nabla E)-k_0^2\left(\varepsilon_{\mathrm{p}}-\frac{j\sigma}{\omega\varepsilon_0}\right)E=0 $$ (1) 式中：k0为微波的波数；E为电场强度；j为电流密度；ω为微波的角频率；μr为相对磁导率；εp为相对介电常数；σ为电导率；ε0为真空介电常数。
对于材料域内的电导率σ和相对介电常数εp的设置：空气区域设为σ=0 S/m，εp=1；石英窗口材料设为σ=1×10−14 S/m，εp=3.78；而在等离子体域内（放电区域），材料电导率σ和相对介电常数εp则跟随着电子密度的变化而变化，其表达式如式（2）、式（3），等离子体的频率如式（4）[11]。
$$ \sigma_{\mathrm{p}}=v_{\mathrm{m}}\frac{\varepsilon_0\omega_{\mathrm{p}}^2}{\omega^2+v_{\mathrm{m}}^2} $$ (2) $$ \varepsilon_{\mathrm{p}}=1-\frac{\omega_{\mathrm{p}}^2}{\omega^2+v_{\mathrm{m}}^2} $$ (3) $$ {\omega }_{\mathrm{p}}^{2}=\frac{{e}^{2}{n}_{\mathrm{e}}}{{\varepsilon }_{0}{m}_{\mathrm{e}}} $$ (4) 式中：ωp为等离子体的频率；vm为电子碰撞频率；ω为微波的频率；e为元电荷；ne为电子密度；me为电子质量。式（5）和式（6）分别为ω和vm的表达式[12-14]：
$$ \omega =2\mathrm{\pi }\times 2.45 $$ (5) $$ v_{\mathrm{m}}=\left(1.08\times10^{10}\right)\frac{p_0}{T_{\mathrm{g}}} $$ (6) 式中： p0为输入压力；Tg为气体温度。
1.2 等离子体模块的计算
由于等离子体内部会发生大量的粒子碰撞，且伴随有复杂的化学反应，因此相较于微波电场来说，等离子体的数值模拟会更复杂。针对该问题，Füner等[14]提出一种新方法来计算电子数密度，从而简化了等离子体计算过程，如式（7）所示：
$$ n_{\mathrm{e}}=\left\{\begin{array}{cc}\gamma(E-E_{\mathrm{M}})+n_{\mathrm{e}_{\mathrm{-}}\mathrm{mi}\mathrm{n}} & \mathrm{ }E > E_{\mathrm{M}} \\ 0 & \mathrm{其}\mathrm{他}\mathrm{情}\mathrm{况}\end{array}\right. $$ (7) 式中：γ为Füner系数；EM为击穿场强；ne_min为电子密度的最小值。Füner的模型简洁明了地表示出了局部电子数密度与局部电场强度之间的线性关系。然而，该线性关系和实际状态存在明显的差异，方程的解通常不会呈平滑状态，该方法也难以实现对次生等离子体转化的模拟。
参考Pleuler团队改进的唯象模型[15]可以有效避免Füner模型中出现的问题，即可以将电子密度视为各种电子生成和损失过程之间达成平衡的产物，同时使用该唯象模型计算电子密度时无须求解大量电子碰撞和反应的微分方程，这使得“唯象法”的计算量显著减少，计算方法如式（8）。
$$ \nabla(-D_{\mathrm{e}}\nabla n_{\mathrm{e}})+R_{\mathrm{v}\mathrm{r}}n_{\mathrm{e}}^2+R_{\mathrm{a}}n_{\mathrm{e}}=R_{\mathrm{i}}E^2n_{\mathrm{e}} $$ (8) 式中：De为电子扩散系数；Ri、Rvr和Ra三个速率系数描述氢分子电离产生电子和电子通过与离子和中性粒子碰撞而消失的过程。Ri的值的设置见参考文献[16]；Rvr的取值[17-18]可以设为10−13 m³/s；Ra的取值[19]设为10−2 s−1，但由于Rane这一项对于方程起不到较大影响，所以可以将其省去。在对MPCVD谐振腔进行唯象模拟时，假设谐振腔处于纯氢气环境中，忽略电子、离子和中性粒子之间复杂的碰撞和反应，从而简化模拟过程[20]。
1.3 流体传热模块的计算
在求解电场和电子密度ne的计算时，可以通过式（9）和式（10）求得等离子体微波的功率密度Qh和气体温度Tg[11，20]。
$$ {Q}_{\mathrm{h}}=\frac{{e}^{2}{v}_{\mathrm{m}}{n}_{\mathrm{e}}{E}^{2}}{2{m}_{\mathrm{e}}({\omega }^{2}+{v}_{\mathrm{m}}^{2})} $$ (9) $$ \nabla(-k\nabla T_{\mathrm{g}})=Q_{\mathrm{h}} $$ (10) 式中： k为热导率。气体温度Tg的分布情况对于等离子体的数值模拟来说是必不可少的，微波的功率密度会随电场、电子密度的变化而变化。
从电磁求解器中求得E的值并代入唯象模型的偏微分方程中用以求解电子密度ne的值，同时也可以求出相应的电导率σ和相对介电常数εp，通过电场和电子密度的解可以求得微波功率密度Qh，将Qh带入传热方程可以得到气体温度Tg的值。至此一个运算流程结束，但为了保证最终结果的自洽性，应将该流程循环多次，即把一次循环得到的解作为下一次循环开始的初始值进行迭代，直到最终结果趋于稳定。
2. MPCVD谐振腔的设计
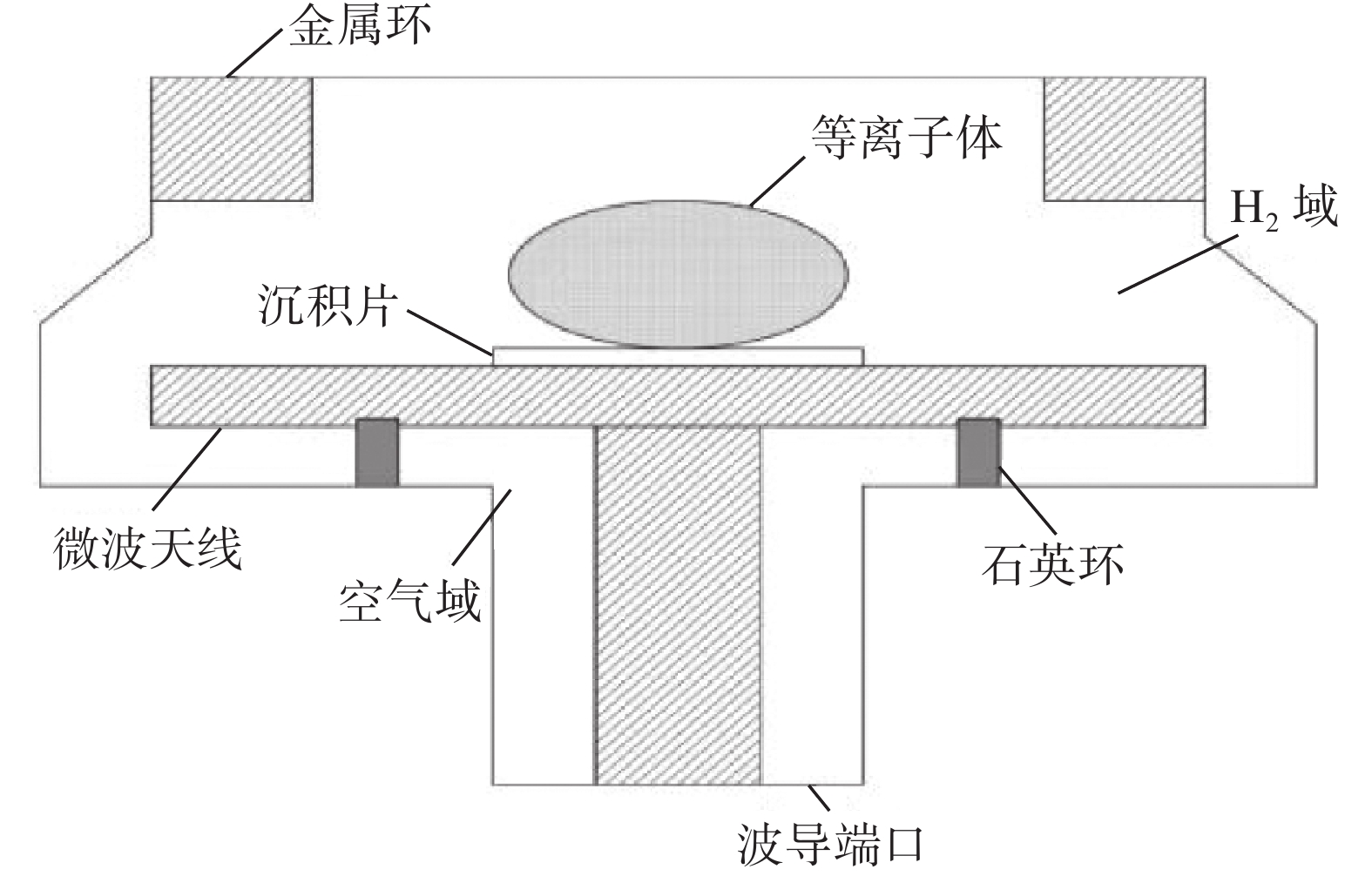
MPCVD谐振腔的设计要考虑到诸多要素，本文主要依据三个准则来进行谐振腔构建。首先选择固定的谐振模式，本文选择电场与波传播方向平行的TM模式，将谐振输入压力的壁看作理想导电表面，根据理想导电表面上电场的边界条件来看，电场的切向分量将为零，电场方向垂直于内壁；然后是耦合方式的选取，本文采取电耦合的方式进行数值模拟，即通过在MPCVD装置内放置电极或天线等元器件，实现微波能量的传输和耦合，该方式实现简单，只需要安置天线就可激发谐振腔的激励模式，同时可以通过天线更方便地对MPCVD装置进行调节，实现对耦合效果的精确控制且存在较好的稳定性和可靠性，耦合效率高；最后进行相应的环口设置，对MPCVD谐振腔内石英环进行合理设计，用来更好地激发等离子体和实现对金刚石膜的沉积，同时避免石英环附近次生等离子体的产生，这就要求要在等离子体域创造一个低压环境，并且只能在这个区域内产生一个强电场来激发等离子体，需要注意的是，石英环附近的场强不能过高以防止石英环被烧坏，且激发出的等离子体不能对石英环造成任何损害。
为了确保构建的MPCVD谐振腔能够达到预期的工作状态，需要对其进行尺寸的优化和改进，具体方案如下。
（1）增大沉积片尺寸：初始电场分布分析显示，当沉积片直径为90 mm时，腔内出现了较多次生场强的区域，导致电场分布不均匀和部分区域场强过高，容易烧坏器件。因此，需要优化腔体尺寸以改善电场分布。
（2）电场线分割[21]和调整：通过对电场线进行分割，特别是在垂直电场线的方向上进行调整，减小了腔体上部的尺寸，同时在腔体中部采用平滑斜面延伸到下部的设计。这一调整有助于减少器件附近的次生电场，提高了电场分布的均匀性和稳定性。
（3）金属环的嵌入：在腔体上部安装金属环，用来进一步调节场强分布。金属环的引入使得腔体内的电场更加集中和均匀，有效消除了新次生电场，从而改善了沉积片表面的电场覆盖情况。
（4）优化的MPCVD谐振腔模型：最终得到的电场分布显示，峰值场强显著提升，达到了能够在沉积片上生成等离子体所需的水平，确定了能够在2.45 GHz频率下工作，并且适应较大沉积片面积。同时，器件附近的次生电场明显减弱，保证了器件的稳定性和可靠性。
使用CST Studio Suite软件对MPCVD谐振腔进行初步设计，在不考虑等离子体效应的情况下，对腔体内电场分布进行仿真分析，通过调试腔体使电场分布满足腔内TM021谐振模式的工作状态。确定了最终的MPCVD谐振腔模型之后，再使用COMSOL Multiphysics有限元模拟软件对MPCVD谐振腔内部电场分布（包括有等离子体效应和无等离子体效应时的电场）、电子密度（等离子体密度）分布和气体温度分布进行数值模拟。
图1为沉积片直径为60 mm时的电场分布，根据初步构建的结果来看，发现该MPCVD谐振腔符合TM021工作模式，考虑到目前市面上大多数MPCVD装置所用的沉积片直径在60 mm左右，且已知的能够在较大直径沉积片下产生等离子体的MPCVD装置通常工作频率为915 MHz。
![]()
图 1 沉积片直径为60 mm时的电场分布Figure 1. Electric field distribution of deposition sheet with diameter of 60 mm本文以增大沉积片面积为目标，对所构建的谐振腔模型进行优化改进，通过数值模拟的方法，设计出一款能够在2.45 GHz下工作的具有较大沉积片面积的MPCVD谐振腔模型，为后续的MPCVD反应器提供参考。
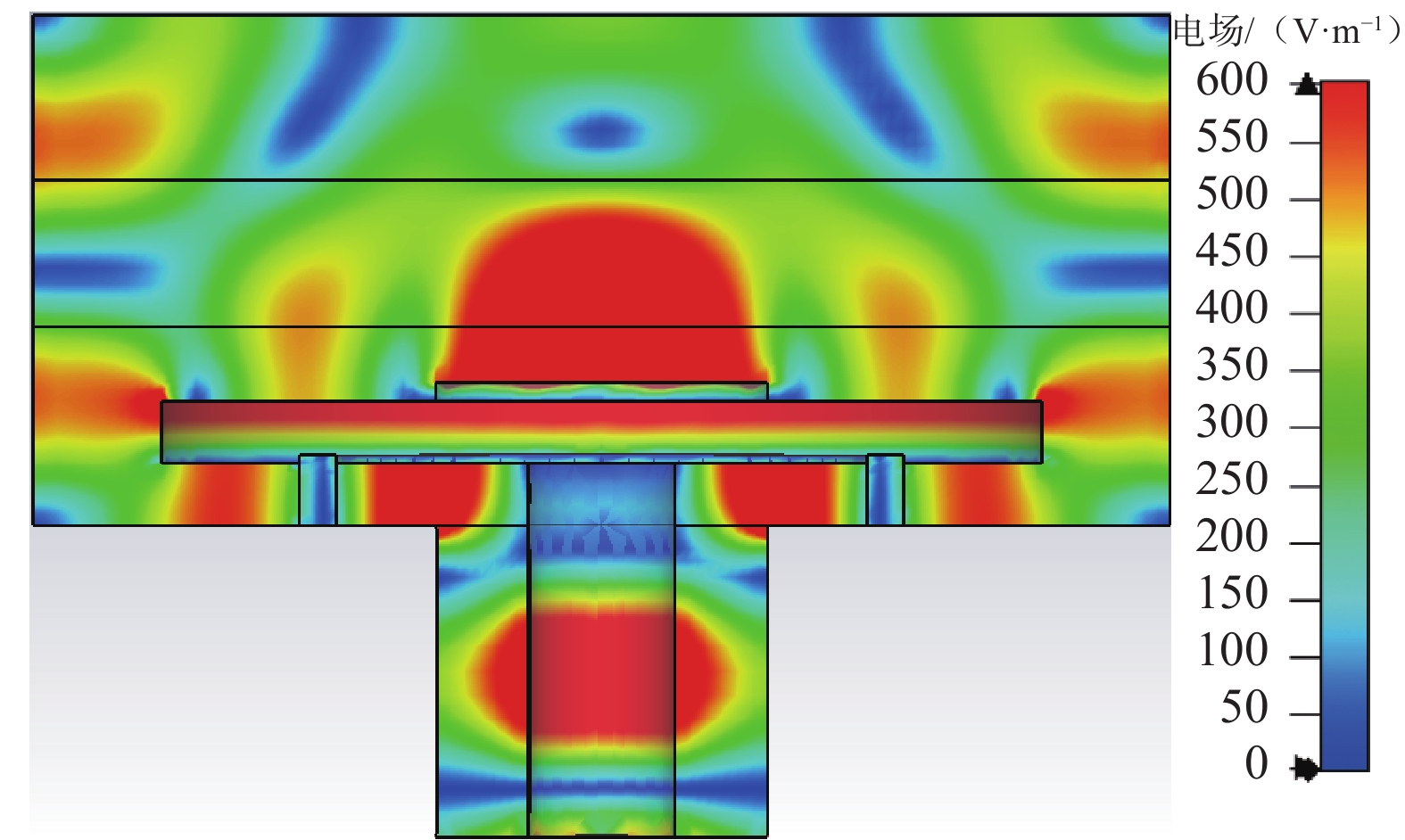
沉积片直径增大至90 mm，对MPCVD谐振腔电场分布进行仿真分析。由图2的结果可知，当沉积片表面被电场覆盖时，腔内产生次生场强的区域较多，从而导致腔内电场分布不均，且天线端和石英环附近的场强容易烧坏器件。同时，观察到场强峰值偏低（仅有600 V/m），而过低的场强可能会导致后续无法在沉积片上产生等离子体。因此尝试采用分割电场线的方法对腔体进行调整。
![]()
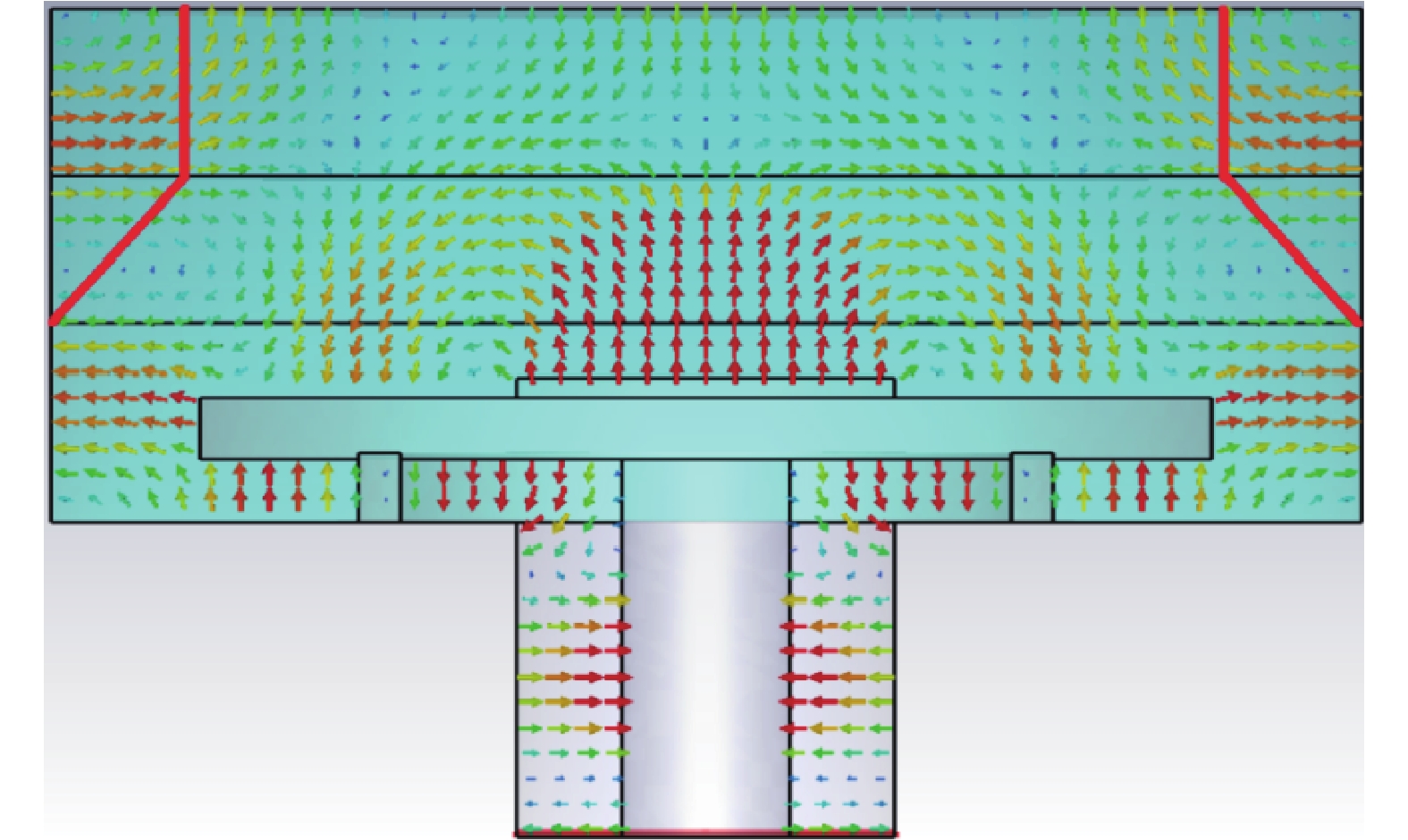
图 2 沉积片直径为90 mm时的电场分布Figure 2. Electric field distribution of deposition sheet with diameter of 90 mm依照图3中的红色分割线，沿垂直电场线的方向对腔体进行分割，减小腔体上部的尺寸，腔体中部以平滑斜面延伸到下部，对分割后的腔体电场分布进行仿真，结果如图4所示。
![]()
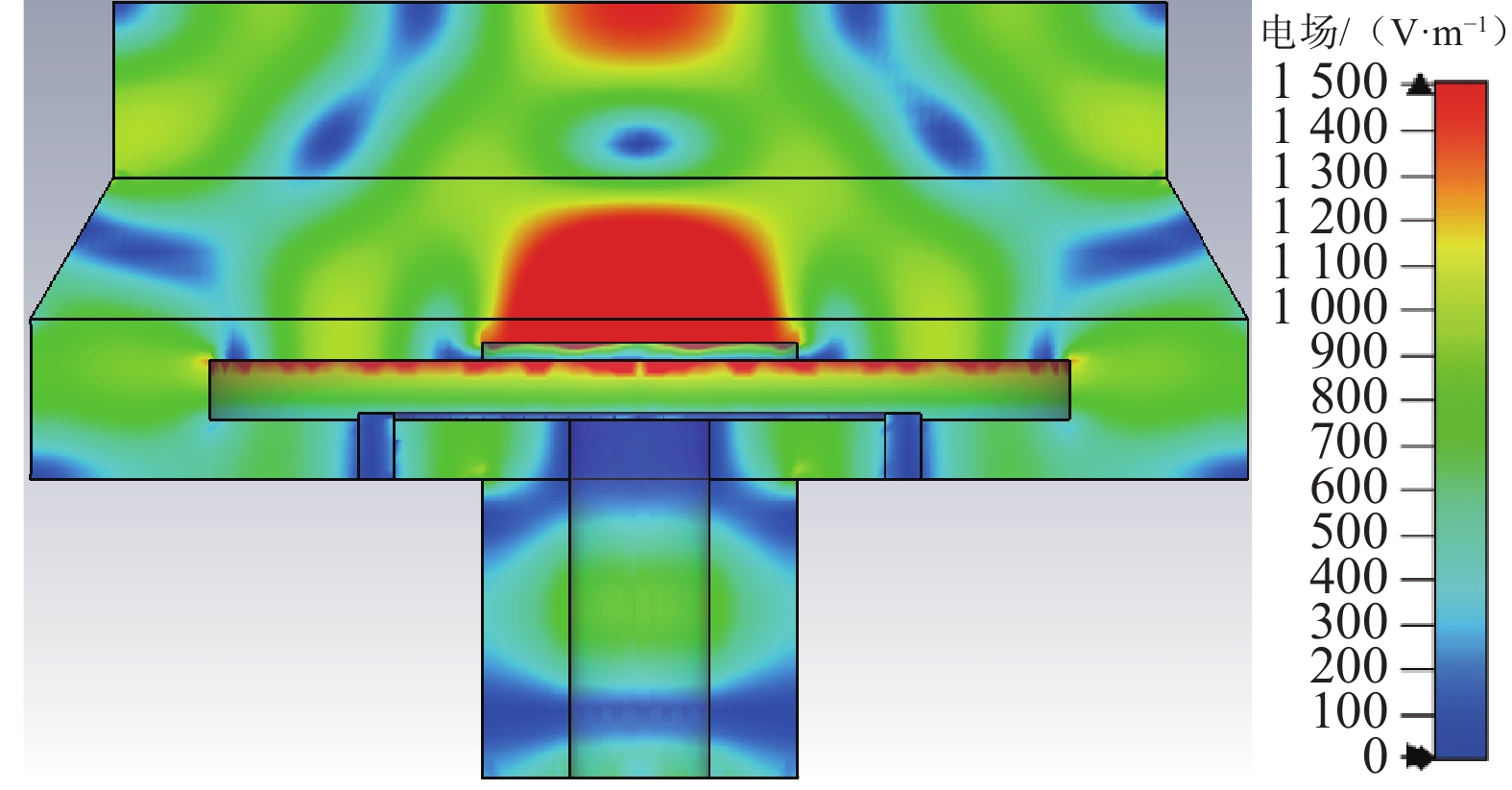
图 3 电场线分布（红线标识为电场分割线）Figure 3. Electric field line distribution（The red line is the electric field divider）根据图4所示电场分布结果发现经分割后的谐振腔内的峰值场强有了明显提升，能更好地在沉积片上生成等离子体，同时器件附近的次生电场明显减弱，天线端和石英环也不会被烧坏。但观察到腔体上方产生了新次生电场。
![]()
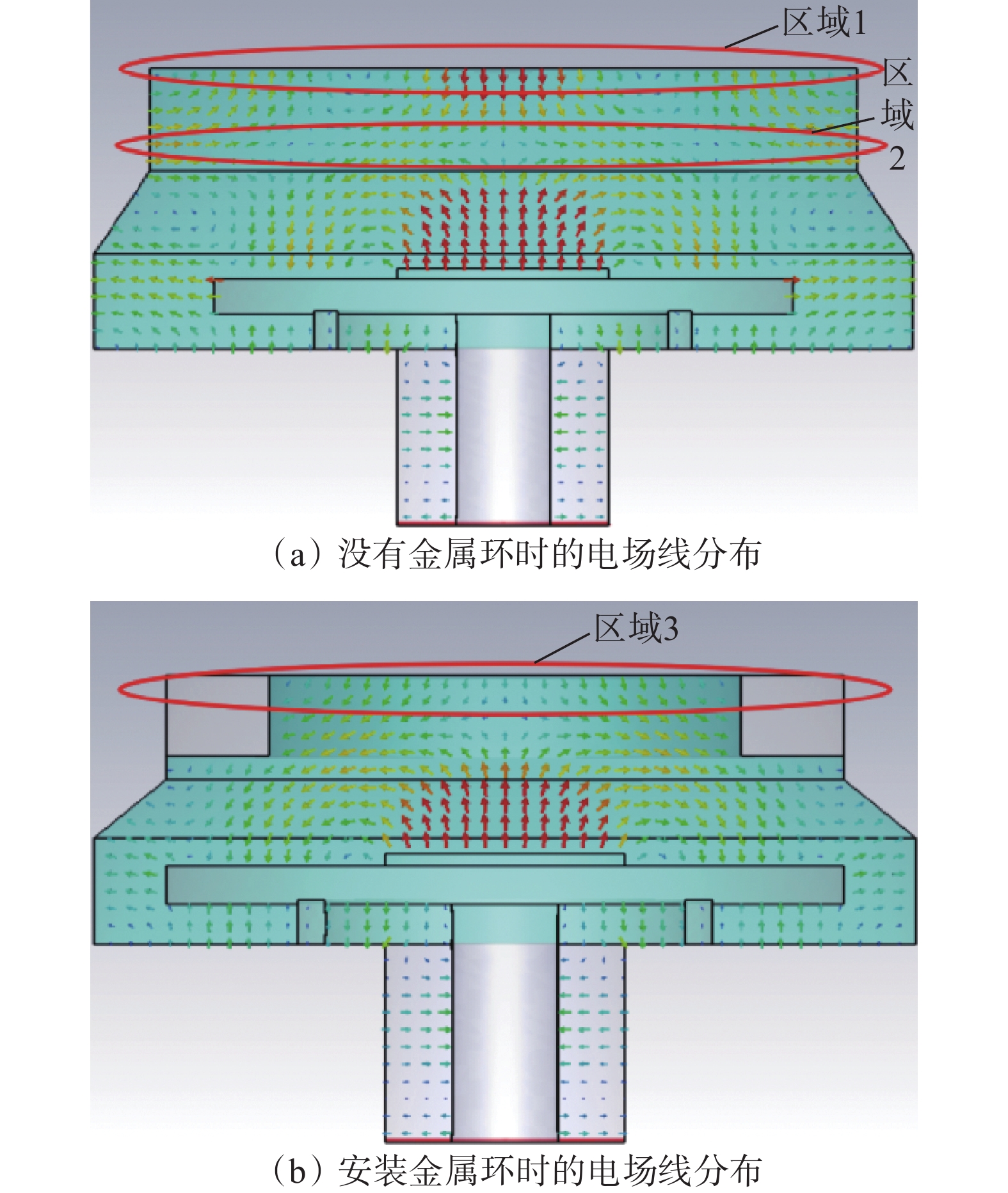
图 4 调整后的MPCVD谐振腔电场分布Figure 4. The adjusted electric field distribution of MPCVD resonator为了消除新次生电场，在谐振腔上部安装上金属环，用来调节腔内电场线分布，如图5所示。
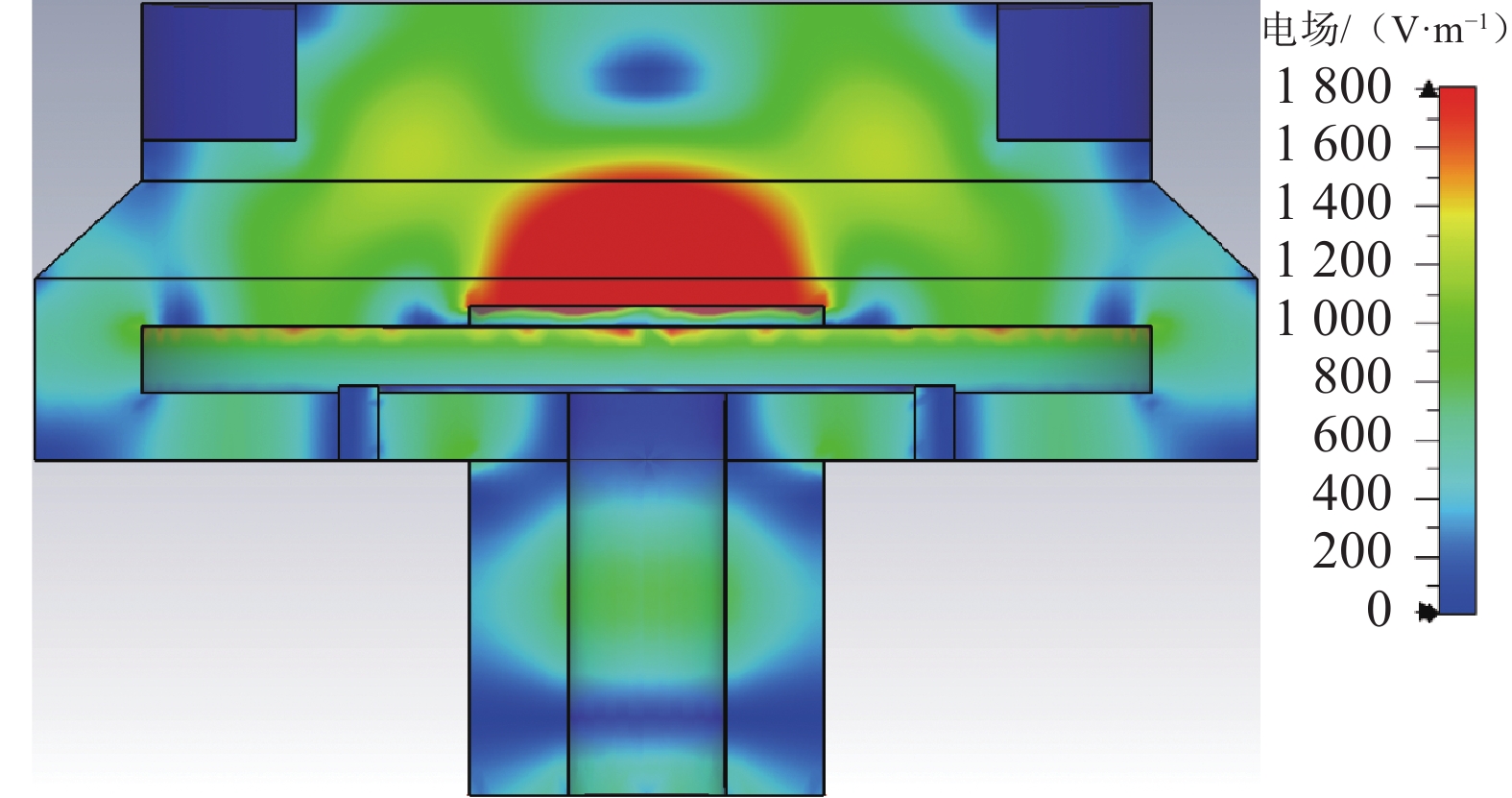
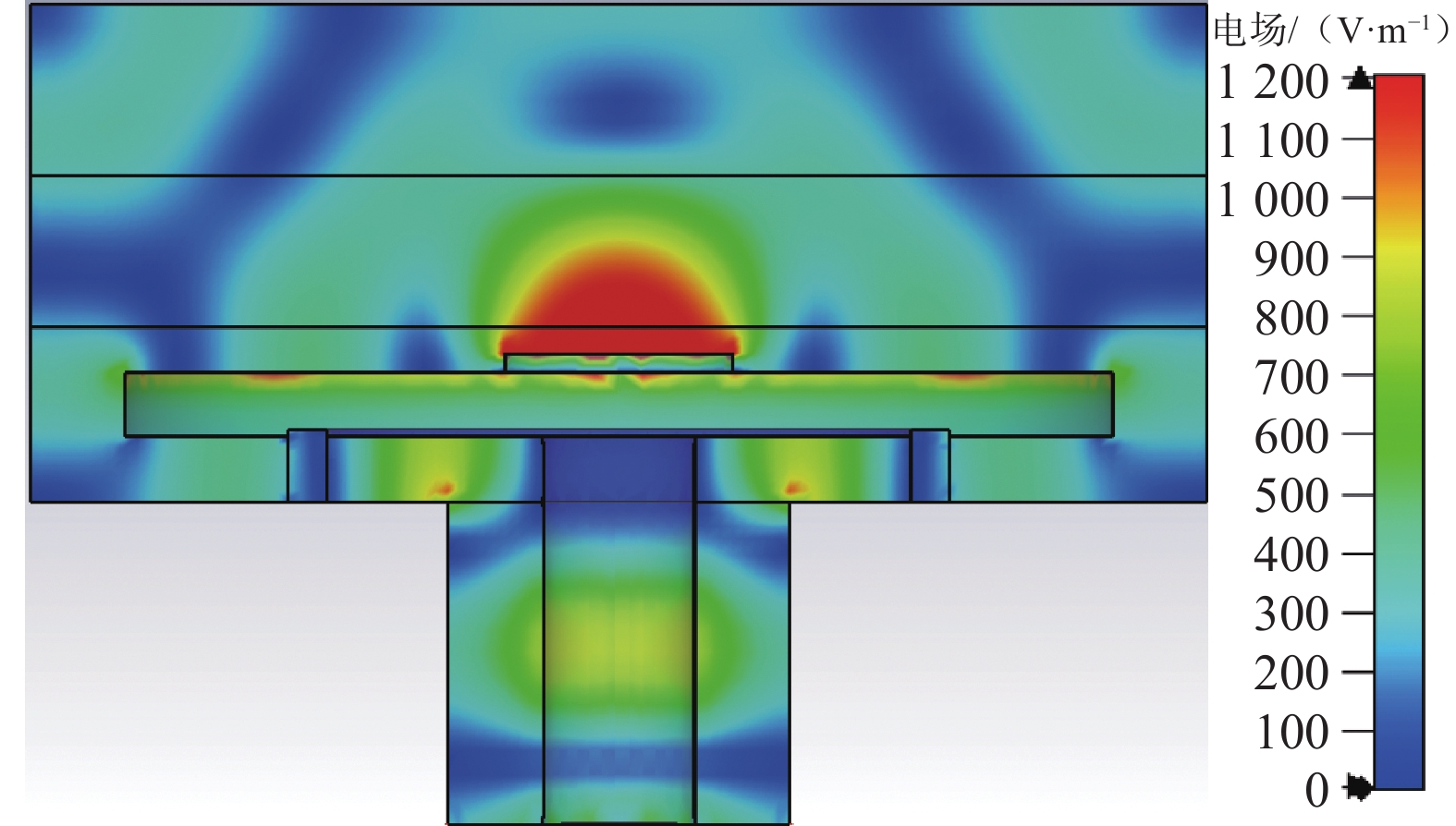
对比图5（a）和图5（b），可以发现区域1的电场线分布随着金属环的加入而消失，区域2与区域3内的电场线分布保持一致，这说明金属环的介入使腔体内电场分布集中上移，从而使得产生的次生电场消失。由于金属环对电场分布的调谐，沉积片上的电场更加集中且均匀，腔内不再产生次生电场，电场分布如图6所示，仿真结果符合预期。最终优化的MPCVD谐振腔模型如图7所示。
![]()
图 6 最终优化的MPCVD谐振腔电场分布Figure 6. Final optimization of electric field distribution in MPCVD resonator3. 结果与讨论
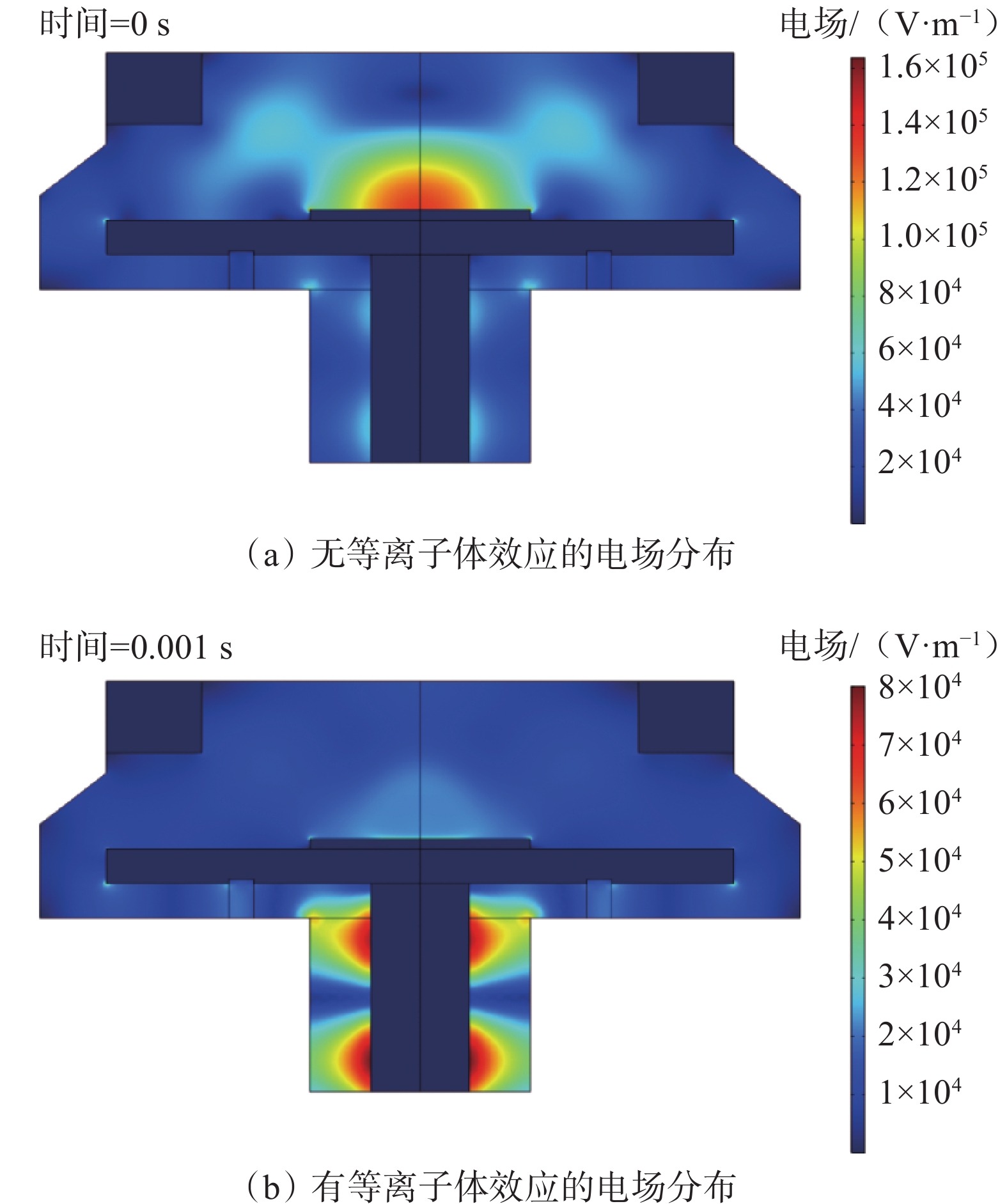
图8（a）为进行电子密度的数值仿真之前，MPCVD腔体内不存在等离子体效应的电场分布结果。图8（b）为完成电子密度的数值仿真后，腔体存在等离子体效应的电场分布结果。通过对比可知，电子密度的产生与微波电场的分布呈负相关，也就是说等离子体的存在会吸收微波，从而导致电场衰减。
微波源功率和输入压力是影响数值模拟的两个重要因素，图9为MPCVD装置在功率
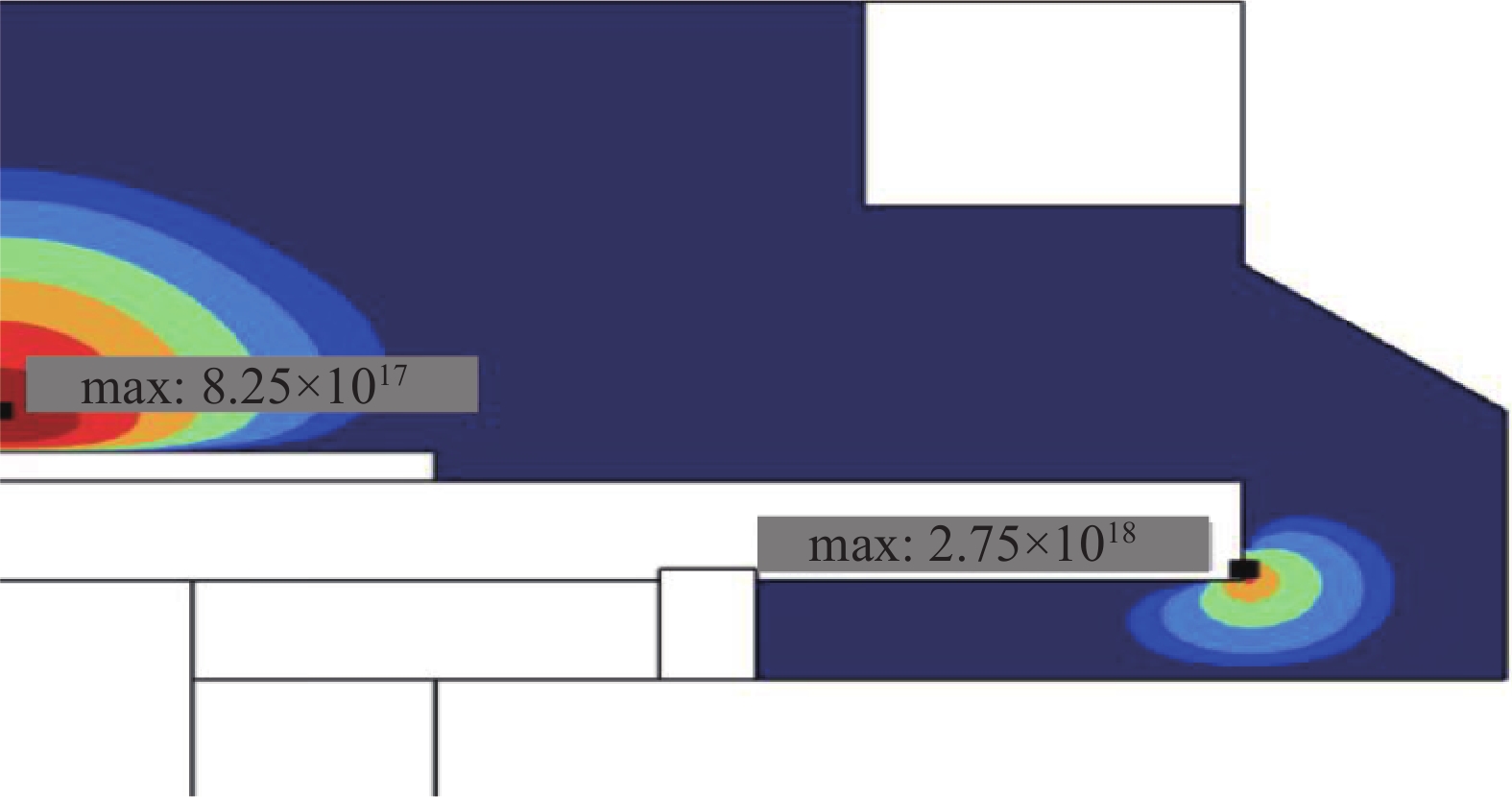
3000 W、压力8 kPa条件下电子密度和温度模拟结果，图10为在该条件下选取的腔内沉积片上方和天线端处电子密度的最大值。可以发现在微波源功率3000 W、输入压力8 kPa的条件下，沉积片上激发的等离子体较少，电子密度最大也仅为8.25×1017 m−3，同时等离子体有着向微波天线聚拢的趋势，以至于在天线末端的电子密度峰值超过沉积片上的电子密度最大值，达到了2.75×1018 m−3。这种结果导致了等离子体的分布不均，并且天线端激发出的次生等离子体会对天线造成刻蚀现象，损坏天线。![]()
图 9 3 000 W、8 kPa条件下的模拟结果Figure 9. The simulation results obtained at3000 W and 8 kPa![]()
图 103000 W、8 kPa条件下沉积片上方和天线端处电子密度的最大值Figure 10. The maximum electron density above the deposited sheet and at the antenna end at3000 W and 8 kPa考虑将微波源功率增大至
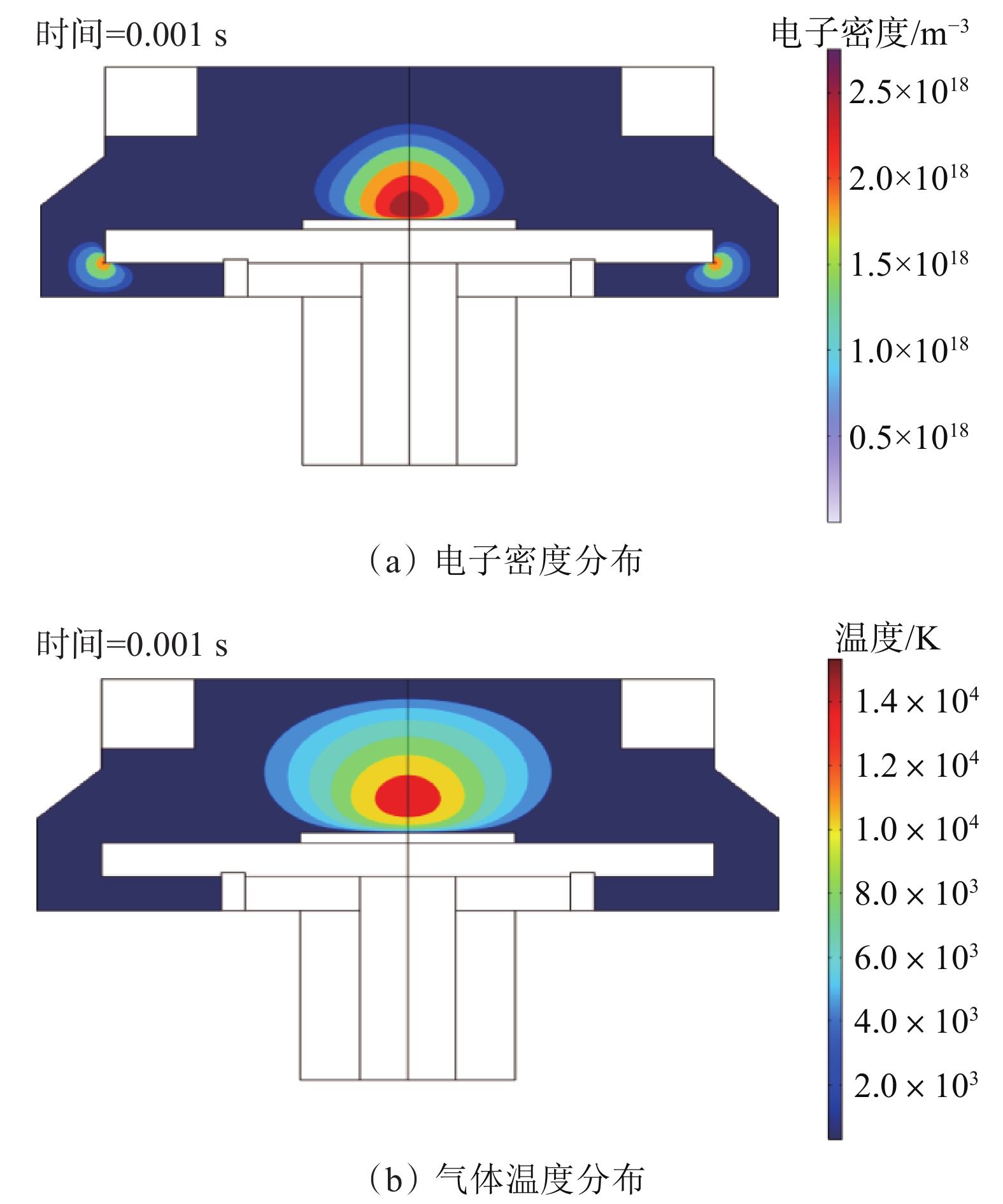
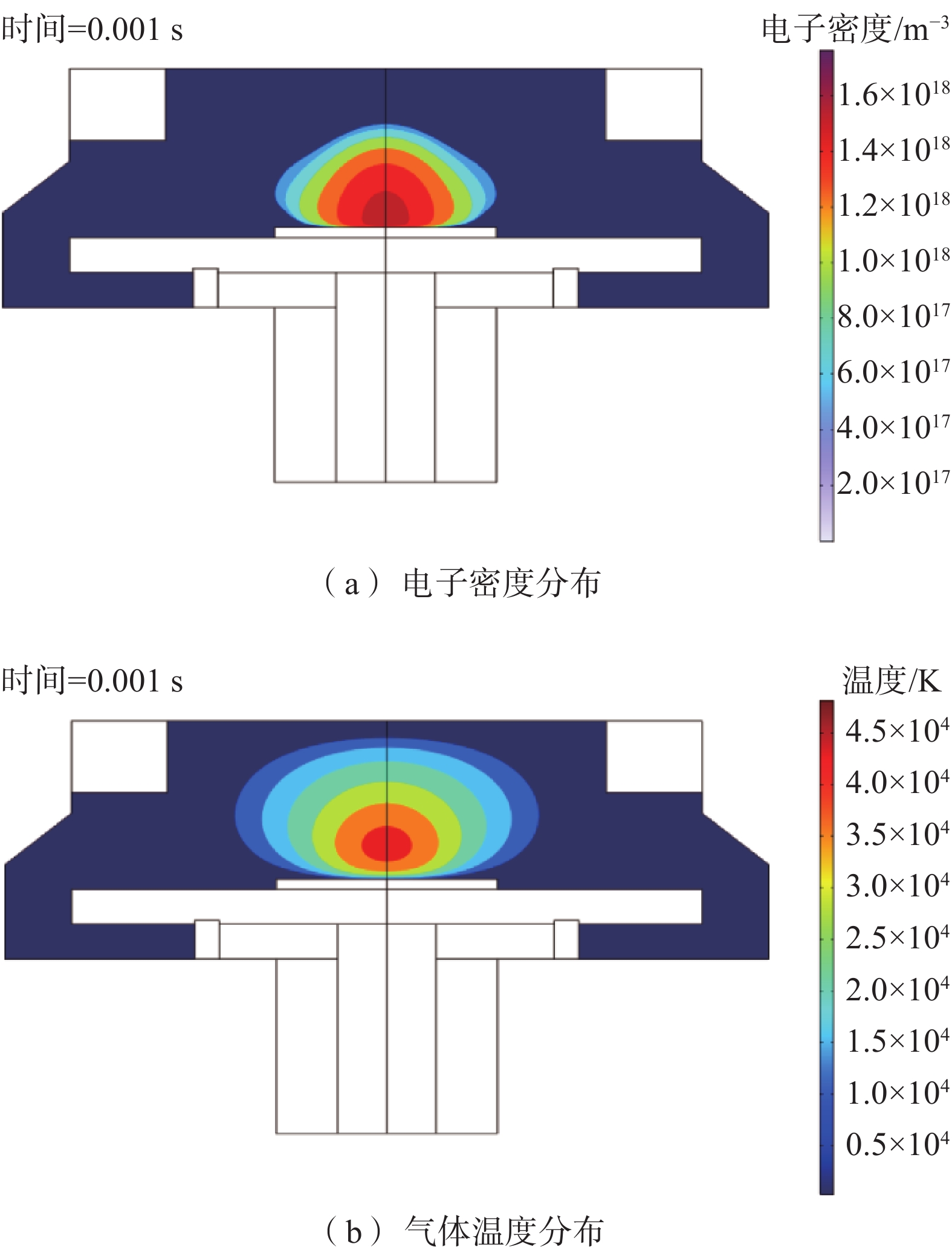
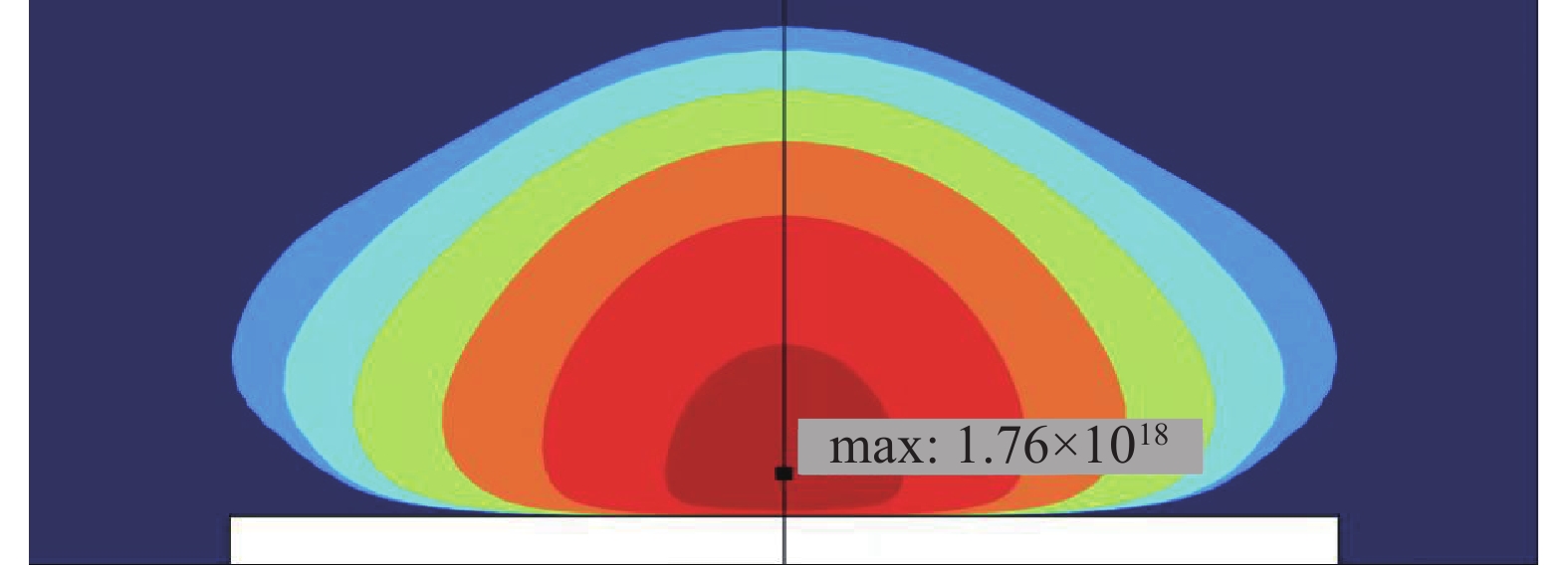
6000 W、输入压力增大至14.7 kPa，模拟结果如图11所示。图12是在此条件下选取的腔内沉积片处的电子密度最大值。可以看到，此时沉积片上激发出的等离子体密度增大，达到了1.76×1018 m−3，并且等离子体分布均匀，没有次生等离子体的产生，因而不会在天线末端形成聚拢和刻蚀，防止了天线受到损害。![]()
图 116000 W、14.7 kPa条件下的模拟结果Figure 11. The simulation results obtained at6000 W and 14.7 kPa![]()
图 126000 W、14.7 kPa 条件下沉积片上电子密度的最大值Figure 12. The maximum electron density on the deposited sheet at6000 W and 14.7 kPa根据仿真结果可知，微波源功率和输入压力与沉积片上所生成的电子密度和气体温度呈现正相关的关系，即随着功率和压力的增加，电子密度和气体温度也随之增加。在
3000 W、8 kPa的条件下，沉积片上的电子密度和气体温度分别约为8.25×1017 m−3和1.5×104 K。当功率增至6000 W，压力增至14.7 kPa时，电子密度和气体温度都有明显的升高，分别约为1.76×1018 m−3和4.7×104 K，这表明较高的微波源功率和输入压力可以产生高密度等离子体，所得气体温度也符合实际应用情况，并且沉积片上仅存在一个等离子体区，没有次生等离子体的出现，电子密度分布与期望结果基本契合。4. 结论
本文设计了一个在2.45 GHz频率下满足TM021谐振工作模式的微波等离子体化学气相沉积（MPCVD）装置，该装置的沉积片直径为90 mm，相较于现有大多数沉积片来说，所得到的沉积膜面积更大。运用数值模拟的方法对所构建的谐振腔进行分析，根据微波电场模拟理论和电子漂移扩散的原理，模拟出微波场强E、电子密度ne以及气体温度Tg等能够反映等离子体特性的参数。通过比对不同微波输入功率、输入压力下所得的电子密度和气体温度的仿真结果，确定了最终微波输入功率为
6000 W，输入压力为14.7 kPa，在该条件下的数值模拟结果显示能很好地抑制了次生等离子体的产生，从而规避了微波天线受损的风险，并且激发出的等离子体能够均匀地分布于沉积片上。该MPCVD谐振腔的设计和数值模拟具有一定的可靠性，为后续较大沉积面积MPCVD装置的实现提供了思路。 -
![]()
图 1 沉积片直径为60 mm时的电场分布
Figure 1. Electric field distribution of deposition sheet with diameter of 60 mm
![]()
图 2 沉积片直径为90 mm时的电场分布
Figure 2. Electric field distribution of deposition sheet with diameter of 90 mm
![]()
图 3 电场线分布（红线标识为电场分割线）
Figure 3. Electric field line distribution（The red line is the electric field divider）
![]()
图 4 调整后的MPCVD谐振腔电场分布
Figure 4. The adjusted electric field distribution of MPCVD resonator
![]()
图 6 最终优化的MPCVD谐振腔电场分布
Figure 6. Final optimization of electric field distribution in MPCVD resonator
![]()
图 9 3 000 W、8 kPa条件下的模拟结果
Figure 9. The simulation results obtained at
3000 W and 8 kPa![]()
图 10
3000 W、8 kPa条件下沉积片上方和天线端处电子密度的最大值Figure 10. The maximum electron density above the deposited sheet and at the antenna end at
3000 W and 8 kPa![]()
图 11
6000 W、14.7 kPa条件下的模拟结果Figure 11. The simulation results obtained at
6000 W and 14.7 kPa -
[1] ITOH H,NAKAMURA T,IWAHARA H. Microstructural control of boundary region between CVD diamond film[J]. Journal of Materials Science,1994,29(5):1404−1410. doi: 10.1007/BF00975095
[2] LIAO Y,FANG R,YE Z Y,et al. Investigation of the thermal conductivity of diamond film on aluminum nitride ceramic[J]. Applied Physics A,1999,69:101−103. doi: 10.1007/s003390050979
[3] YANG Q,YANG S L,XIAO C,et al. Effects of nickel thin films on nucleation and growth of diamond on silicon substrates[J]. Materials Research Innovations,2006,10(4):408−410. doi: 10.1179/143307507X199380
[4] XU Z Q,ASHOK S K,ARUN K. Amperometric detection of glucose using a modified nitrogen-doped nanocrystalline diamond electrode[J]. Journal of Biomedical Nanotechnology,2005,1(4):416−420. doi: 10.1166/jbn.2005.057
[5] NAKAI T,ARIMA K,MAIDA O,et al. High-quality diamond films grown at high deposition rates using high-power-density MWPCVD method with conventional quartz-type chamber[J]. Journal of Crystal Growth,2007,309(2):134−139. doi: 10.1016/j.jcrysgro.2007.09.024
[6] ASMUSSEN J,GROTJOHN T A,SCHUELKE T,et al. Multiple substrate microwave plasma-assisted chemical vapor deposition single crystal diamond synthesis[J]. Applied Physics Letters,2008,93(3):031502. doi: 10.1063/1.2961016
[7] ZUO S S,YARAN M K,GROTJOHN T A,et al. Investigation of diamond deposition uniformity and quality for freestanding film and substrate applications[J]. Diamond and Related Materials,2008,17(3):300−305. doi: 10.1016/j.diamond.2007.12.069
[8] HASSOUNI K,SILVA F,GICQUEL A. Modelling of diamond deposition microwave cavity generated plasmas[J]. Journal of Physics D:Applied Physics,2010,43(15):153001. doi: 10.1088/0022-3727/43/15/153001
[9] GICQUEL A,HASSOUNI K,BRETON Y,et al. Gas temperature measurements by laser spectroscopic techniques and by optical emission spectroscopy[J]. Diamond and Related Materials,1996,5(3/5):366−372. doi: 10.1016/0925-9635(95)00429-7
[10] GICQUEL A,CHENEVIER M,HASSOUNI K H,et al. Validation of actinometry for estimating relative hydrogen atom densities and electron energy evolution in plasma assisted diamond deposition reactors[J]. Journal of Applied Physics,1998,83(12):7504−7521. doi: 10.1063/1.367514
[11] SU J J,LI Y F,LI X L,et al. A novel microwave plasma reactor with a unique structure for chemical vapor deposition of diamond films[J]. Diamond and Related Materials,2014(42):28−32.
[12] YAMADA H,CHAYAHARA A,MOKUNO Y,et al. Qualitative correspondences of experimentally obtained growth rates and morphology of single-crystal diamond with numerical predictions of plasma and gas dynamics in microwave discharges for various substrate holder shapes[J]. Japanese Journal of Applied Physics,2006,45(10B):8177.
[13] TAN W,GROTJOHN T A. Modelling the electromagnetic field and plasma discharge in a microwave plasma diamond deposition reactor[J]. Diamond and Related Materials,1995,4(9):1145−1154. doi: 10.1016/0925-9635(95)00291-X
[14] FÜNER M,WILD C,KOIDL P. Simulation and development of optimized microwave plasma reactors for diamond deposition[J]. Surface and Coatings Technology,1999,116/119(9):853−862.
[15] PLEULER E,WILD C,FÜNER M,et al. The CAP-reactor,a novel microwave CVD system for diamond deposition[J]. Diamond and Related Materials,2002,11(3/6):467−471. doi: 10.1016/S0925-9635(01)00731-2
[16] SU J J,LI Y F,DING M H,et al. A dome-shaped cavity type microwave plasma chemical vapor deposition reactor for diamond films deposition[J]. Vacuum,2014,107:51−55. doi: 10.1016/j.vacuum.2014.04.002
[17] SURENDRA M,GRAVES D B,PLANO L S. Self-consistent dc glow-discharge simulations applied to diamond film deposition reactors[J]. Journal of Applied Physics,1992,71(10):5189−5198. doi: 10.1063/1.350575
[18] SCOTT C D,FARHAT S,GICQUEL A,et al. Determining electron temperature and density in a hydrogen microwave plasma[J]. Journal of Thermophysics and Heat Transfer,1996,10(3):426. doi: 10.2514/3.807
[19] SU J,LI Y,LIU Y,et al. Development of cylinderical cavity type microwave plasma CVD reactor for diamond films deposition[C]//IEEE International Pulsed Power Conference(PPC),2013.
[20] LI Y F,AN X M,LIU X C,et al. A 915 MHz/75 kW cylindrical cavity type microwave plasma chemical vapor deposition reactor with a ladder-shaped circumferential antenna developed for growing large area diamond films[J]. Diamond and Related Materials,2017,78:67−72. doi: 10.1016/j.diamond.2017.08.007
[21] LI Y F,SU J J,LIU Y Q,et al. Design of a new TM021 mode cavity type MPCVD reactor for diamond film deposition[J]. Diamond and Related Materials,2014,44:88−94. doi: 10.1016/j.diamond.2014.02.010
下载:
计量
- 文章访问数: 16
- HTML全文浏览量: 3
- PDF下载量: 8
