0.   引言

溅射离子泵是一种气体捕集类真空获得设备。自1958年Hall完成了对溅射离子泵的改良后，溅射离子泵由单筒结构，改为了多筒结构，抽气性能得到大幅提升，广泛应用于航空航天、物理实验等诸多领域中^[1]。

目前，关于溅射离子泵抽速的理论计算已形成较为完备的体系，但这些理论大多基于经验公式进行计算。相比之下，利用模拟仿真方法对溅射离子泵抽速进行研究的相关理论尚未完善，且该领域的研究仍有较大的发展空间。Malev等^[2]根据Popov的潘宁放电理论首次给出了计算溅射离子泵抽速以及溅射离子泵极限压力的方法，但该方法并未考虑阴极板与阳极筒之间的间隔对抽速的影响，且在工作压力较低的情况下误差较大。Hartwig等^[3]根据Suhuurman的放电理论给出了一种较为完备的溅射离子泵抽速计算方法，该方法通过磁场强度判断潘宁放电模式，进而计算单个潘宁放电单元的理论抽速，但该方法并未考虑离子入射后产生的溅射产额对抽速的影响，存在一定误差。何炜等^[4]总结前人理论，根据Suhuurman气体放电理论，Sigmund溅射理论和Langmuir的吸附理论给出了一种更加准确的计算抽速的方法，但是在该方法中入射离子的入射参数差异未被考虑。宁久鑫等^[5]通过使用COMSOL软件模拟潘宁放电过程与离子入射过程，通过离子电流计算了溅射离子泵抽速，但在低压力环境下采用COMSOL的流体力学模型模拟等离子体会出现较大误差。Ha等^[6]采用PIC-MCC算法OOPIC分析了单一压力下入射阴极板的氮气离子分布，并计算了相应的溅射产额，但没有给出不同工作压力下溅射离子泵的抽速变化。耿健等^[7]使用VSIM的二维模型模拟潘宁放电，通过PIC-MCC方法得到了入射离子的入射能量、入射角度等入射参数，并结合何炜等的计算方法计算出溅射离子泵抽速，但二维模型可能会对潘宁放电结果带来一定误差，需要在其基础上，使用三维模型进行模拟。

本文使用基于OpenFOAM开发的PIC-MCC模拟代码picFoam^[8]对溅射离子泵单个潘宁放电单元进行模拟，并结合现有理论计算，总结PIC-MCC计算溅射离子泵的抽速的方法。并通过统计模拟结果，分析离子入射参数分布对溅射离子泵抽速的影响。

1.   PIC-MCC理论

1.1   粒子碰撞模型

在以氮气为背景气体的潘宁放电空间中，存在以下粒子：（1）电子e、（2）氮气离子N₂⁺、（3）氮气离子N₂⁺⁺、（4）氮离子N⁺以及（5）中性气体分子N₂。由于碰撞产生氮气离子N₂⁺⁺以及氮离子N⁺所需电子能量较大，故不考虑空间中N₂⁺⁺以及N⁺的存在^[9]。在PIC-MCC方法中并不需要考虑空间中存在的所有碰撞，可使用Tomonor等^[10]的方法通过计算不同物质之间的密度比，判断可以忽略的碰撞反应。

经过计算，在10⁻⁵~10⁻³ Pa工作压力范围内，需要考虑的碰撞反应为：电子与氮气分子的电离碰撞 e + N₂ →N₂⁺ + 2e ，电子与氮气分子的弹性碰撞e + N₂ →N₂ + e ，电子与氮气分子的激发碰撞e + N₂ → N₂^* + e ，电子与电子的碰撞： e + e→ e + e^[11]。

1.1.1   库伦碰撞模型

潘宁放电中电子与电子之间的库伦碰撞是单个电子失去能量的主要途径^[12]。在PIC-MCC方法中，带电粒子之间的碰撞采用Nanbu提出的方法进行计算。在这种方法中，粒子之间的多次小散射角碰撞被累计为一种独特的大散射角碰撞。这种计算方法需要模拟空间中碰撞粒子足够多，且由于在速度的计算中，假设粒子为非相对论状态，并采用了非相对论状态下的计算公式，因此需要空间中粒子不处于相对论状态^[13]。

在溅射离子泵潘宁放电的模拟中，电子的数量较多且平均能量约为300 eV，未处于相对论状态。基于这样的特性，Nanbu 的计算方法能够在潘宁放电模拟中展现出良好的适用性。

1.1.2   电子与中性分子的碰撞

作为潘宁放电中离子的主要来源，电子与中性分子的碰撞的计算影响着溅射离子泵的抽速计算精准度。

在picFoam中，电子与中性分子之间的碰撞计算使用了无碰撞方法^[14]，这种方法根据单个粒子不发生碰撞所经历的时间分布来计算单个粒子发生碰撞的概率。粒子碰撞后的速度以及电离碰撞后产生的电子速度通过对粒子碰撞前能量进行随机分配得到。

无碰撞方法适用于在均匀电场下的粒子碰撞计算，在溅射离子泵的潘宁放电模拟中，由于溅射离子泵中所加的电场远大于放电过程中等离子体本身产生的电磁场，电场随时间的变化较小，因此无碰撞方法适用于溅射离子泵的潘宁放电模拟。

1.2   仿真模型

1.2.1   几何模型

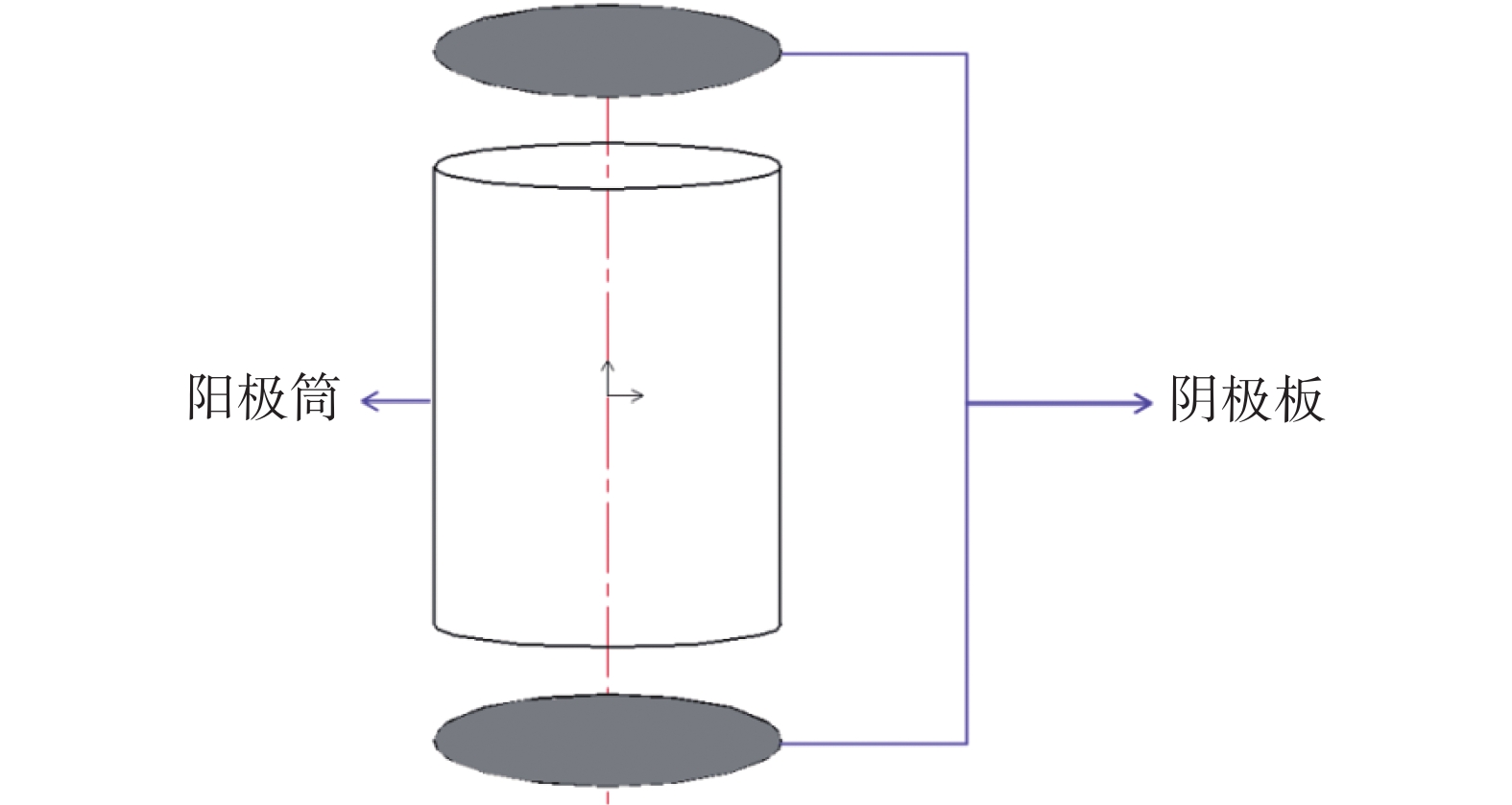
单个潘宁放电单元采取经典的圆筒状阳极结构^[15]，该溅射离子泵单个潘宁放电单元如图1所示，模拟空间由阳极筒、阴极板组成，潘宁放电单元中的具体参数如表1所列。

图  1  溅射离子泵中单个潘宁放电单元几何结构

Figure  1.  Geometric structure of a single Penning discharge unit in a sputtering ion pump

下载: 全尺寸图片 幻灯片

表  1  溅射离子泵单个潘宁放电单元参数

Table  1.  Parameters of a single Penning discharge unit in a sputtering ion pump

尺寸名称	值
阳极筒半径/mm	10
阴阳极间距/mm	6
阳极筒长度/mm	19
磁感应强度/T	0.15
工作电压/V	5 000

下载: 导出CSV 

| 显示表格

在溅射离子泵的实际工作中，由于阳极、阴极外接电路，阳极与阴极的电压稳定保持不变，因此在picFoam的模拟中对阳极、阴极边界选择恒定电压模型，保证阳极、阴极电压稳定不变。

1.2.2   网格划分

在进行仿真前需要对几何模型进行网格划分，对于PIC-MCC方法，需要保证模拟空间内网格长度小于等离子体的德拜长度$ {\lambda _{\text{D}}} $^[16]。在5000 V电压的条件下平均电子温度$ T $约为300 eV，电子在空间中的电子最大密度$ {n_{\text{e}}} $约为2×10¹⁶ m⁻³，平均密度$ \overline {{n_{\text{e}}}} $为3.5×10¹⁵ m⁻³。计算得到潘宁放电等离子体的德拜长度$ {\lambda _{\text{D}}} $约为0.875 mm，即在模拟空间中网格的最大尺寸应该小于0.875 mm。使用网格划分软件ICEM绘制结构化网格，空间中网格平均尺寸为0.37 mm，最大网格尺寸为0.51 mm，符合要求。

1.2.3   边界条件

溅射离子泵潘宁放电模拟的时间步长$ \Delta t $由等离子体的等离子体频率$ {\omega _{\text{p}}} $、电子回旋频率$ {\omega _{\text{e}}} $约束。潘宁放电模拟的时间步长$ \Delta t $与电子等离子体频率$ {\omega _{\text{p}}} $的乘积应小于0.2，与电子回旋频率$ {\omega _{\text{p}}} $的乘积也应小于0.2。通过计算得到等离子体频率$ {\omega _{\text{p}}} $为2.5×10⁹ rad/s，电子回旋频率$ {\omega _{\text{e}}} $为2.89×10⁹ rad/s，即潘宁放电模拟的时间步长应小于7.9×10^-11 s与6.9×10⁻¹¹ s，最终选取时间步长为1×10⁻¹¹ s。

2.   溅射离子泵抽速计算方法

在通过仿真模拟获得离子电流（入射离子数）以及离子的入射参数等相关参数后，需要通过这些参数对溅射离子泵抽速进行计算。根据Jepesen的分析，溅射离子泵在稳定状态下抽除氮气的主要工作原理是附着在阳极筒壁上钛原子对氮气分子的化学吸附，因而在计算对氮气的抽速时只需考虑附着在阳极筒壁上的钛原子对氮气的化学吸附即可^[17]。

2.1   附着在阳极筒壁上的活性钛原子数计算

在离子入射阴极板（钛板）后，阴极板表面的钛原子被溅射出来，被溅射出的原子数目被称为溅射产额。溅射产额与离子入射参数相关，对于溅射产额的计算，使用优化的Sigmund溅射理论^[18-19]计算离子入射时的溅射产额$ Y(\varphi ) $。

根据Ha等^[6]的理论，被溅射出钛原子附着在阳极筒壁上的概率与其被溅射出的位置$ r $有关，即为$ J(r) $。

结合从阴极板被溅射出的钛原子数，可以计算得到附着在阳极筒壁上的活性钛原子数，将不同半径下的溅射产额$ Y(r) $与附着概率$ J(r) $的乘积累加，得到附着在阳极筒壁上的活性钛原子数$ {N_{{\text{Ti}}}} $。

2.2   单个潘宁放电单元抽速计算

计算单个潘宁放电抽气单元的抽速，采用何炜等^[4]的理论，阳极壁面上钛原子覆盖率保持动态平衡。平衡状态下阳极壁面上每秒吸附的氮气分子数$ N\mathrm{\mathit{\mathrm{_{\mathit{\mathrm{a}}}}}} $应等于溅射出的钛原子每秒所覆盖的氮原子数$ N\mathrm{_{\mathit{\mathrm{b}}}} $，以此建立方程并对其求解，溅射离子泵单个潘宁放电单元对氮气的抽速$ s $为：

式中：$ s $为溅射离子泵单个潘宁放电单元对氮气的抽速，L/s；$ g $为辅助参数，$ g=3\times10^{-23}\dfrac{N\mathrm{_{Ti}}}{AP} $；p为工作压力，Pa；$ A $为阳极壁面面积，m²。

至此，通过仿真结果与其他相关参数计算得到了溅射离子泵单个潘宁放电单元对氮气的抽速。

2.3   对单个潘宁放电单元抽速修正

以上计算只考虑了阳极壁面上活性钛原子对氮气分子的吸附速率，并没有考虑放气现象对潘宁放电单元的影响。在实际工作中，当放电空间内的放电强度过大，空间温度会随之上升，阳极壁面的放气现象会加剧，会对抽速产生较大的影响。因此，为了进一步提高抽速计算的精准度，需要考虑放气现象对抽速的影响。

使用COMSOL中的传热模块与电流模块，模拟获得溅射离子泵工作时的温度。温度模拟中所需要的放电强度，通过积累轰击到阳极、阴极的带电粒子获得。获得溅射离子泵工作温度后，计算获得阳极表面的放气量^[20]，修正后的抽速即为2.2节中计算结果与放气量的差值。

2.4   溅射离子泵抽速计算

在实际工作中溅射离子泵内部有多个潘宁放电单元进行抽气工作，在计算溅射离子泵整体抽速时可以认为所有相同的放电单元拥有相同的抽速，结合Hartwig的流导修正模型^[2]，溅射离子泵的整体抽速$ S\mathrm{_{eff}} $即为：

式中：$ S\mathrm{_{eff}} $为溅射离子泵的整体抽速，L/s；$ n $为溅射离子泵中阳极筒数量；$ D $为流导系数。

流导系数$ D $与抽气单元参数有关。抽气单元是指多个阳极筒排列组成的结构，单个抽气单元有着多个潘宁放电单元。

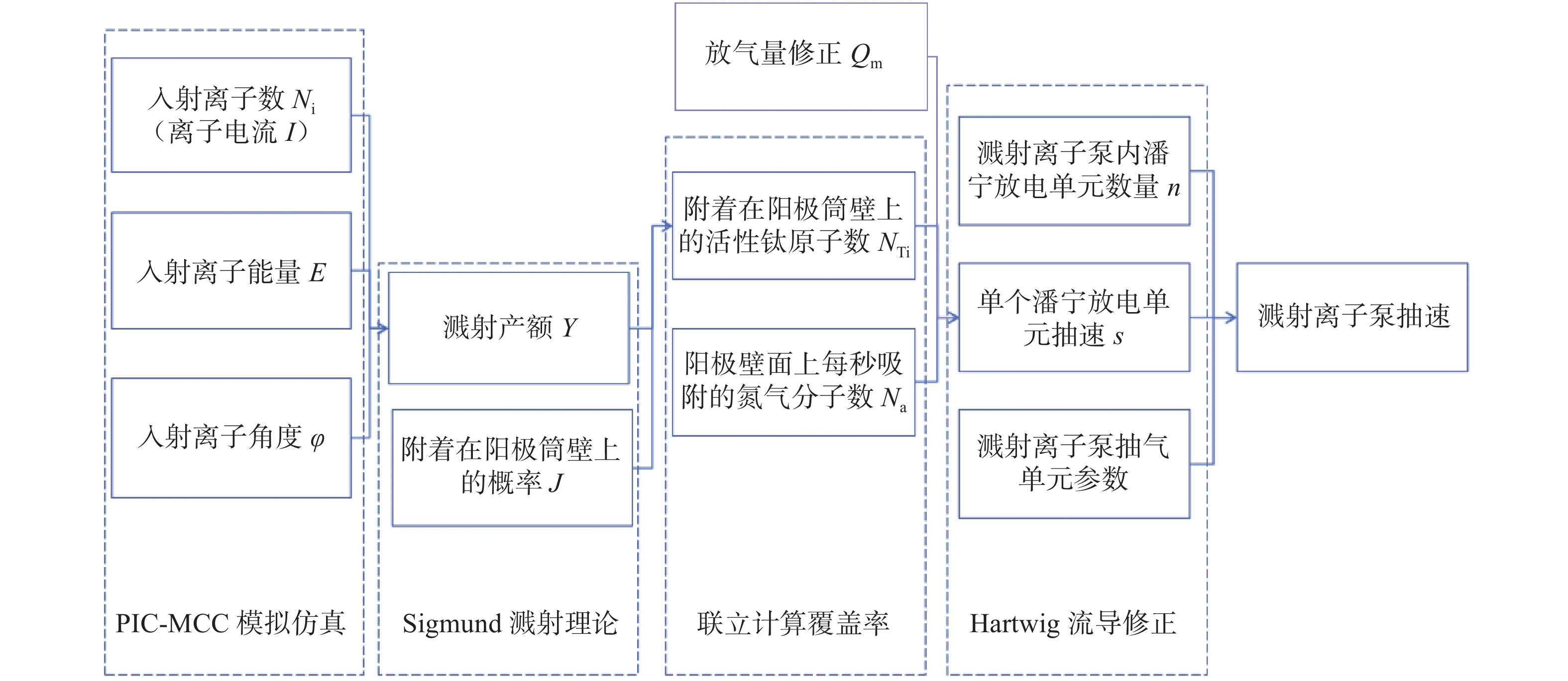
2.5   计算过程与步骤

溅射离子泵抽速计算方法的流程如图2所示，通过模拟方法得到入射离子参数，并计算溅射产额，获得附着在阳极筒壁上的活性钛原子数。结合阳极壁面的放气量，计算单个潘宁放电单元抽速。最后通过流导修正，对溅射离子泵整体抽速进行计算。

图  2  溅射离子泵抽速计算方法的流程图

Figure  2.  Flowchart of calculation method for sputtering ion pump pumping speed

下载: 全尺寸图片 幻灯片

3.   结果与分析

3.1   离子电流

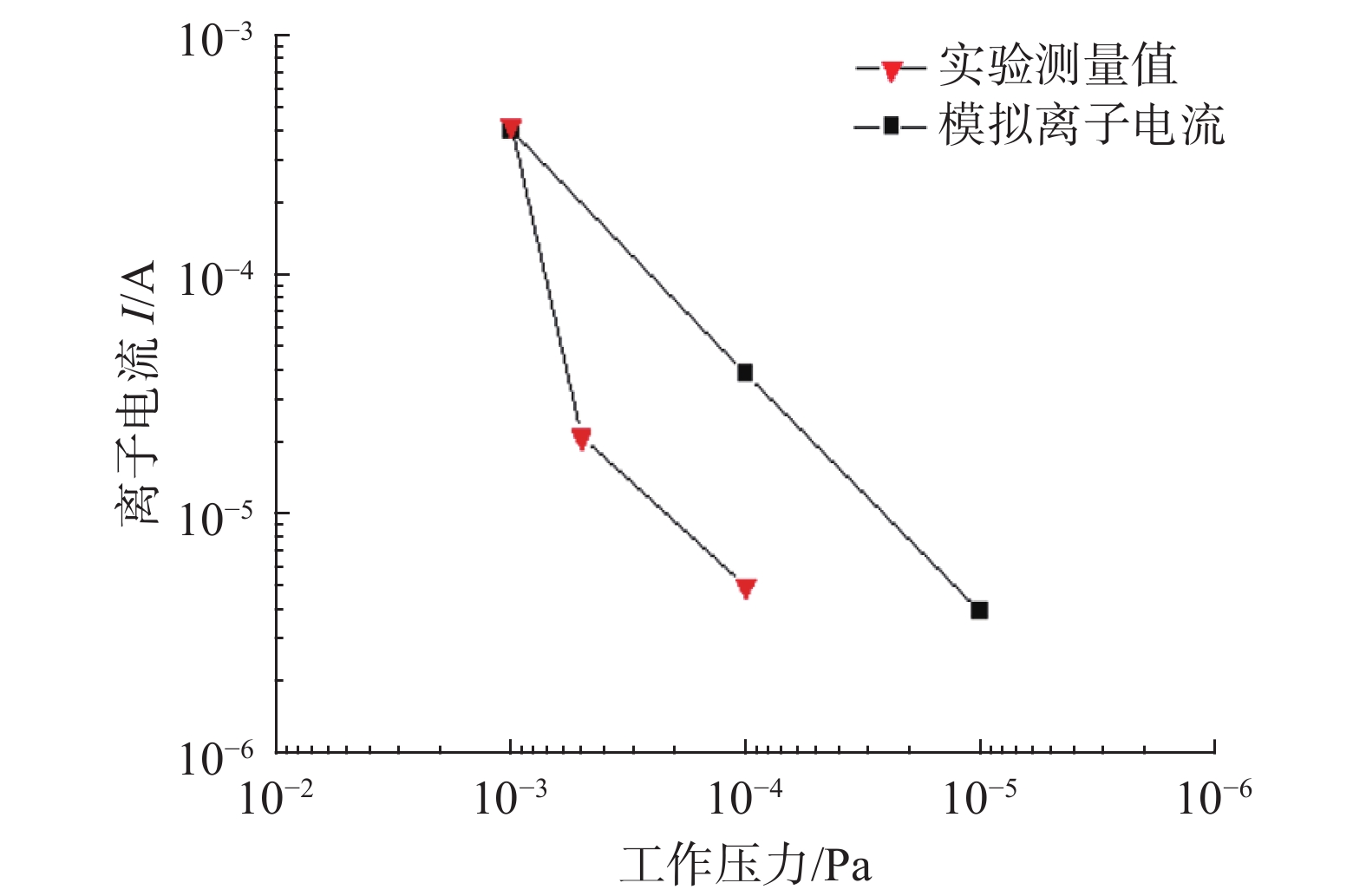
离子电流是表征溅射离子泵工作性能的重要指标，由离子在电磁场的作用下轰击阴极产生。在仿真计算中，离子电流通过统计入射离子数得到，即入射离子数与点电荷的乘积。而在实验测试中，电流通过测量整个放电回路的电流得到，即为电子电流与离子电流的和，这也是实验测试值偏小的原因，如图3～6所示。

图  3  不同工作压力下的离子电流

Figure  3.  Ionic currents under different working pressures

下载: 全尺寸图片 幻灯片

图  4  不同工作压力下的离子入射密度分布

Figure  4.  Ion incidence density distribution under different working pressures

下载: 全尺寸图片 幻灯片

图  5  不同工作压力下的离子入射能量分布

Figure  5.  Distribution of ion incident energy under different working pressures

下载: 全尺寸图片 幻灯片

图  6  不同工作压力下的离子入射角度分布

Figure  6.  Distribution of ion incidence angles under different working pressures

下载: 全尺寸图片 幻灯片

将通过仿真模拟获得的离子电流与耿健等^[7]的实验结果相对比，对比结果如图3所示，仿真电流与实验测量结果变化趋势相似，都是随着工作压力的下降而减小。

3.2   入射参数

离子入射阴极后的入射参数对溅射离子泵的抽速起着关键作用，为了获得更加准确的结果，需要对入射参数的分布进行分析与讨论。

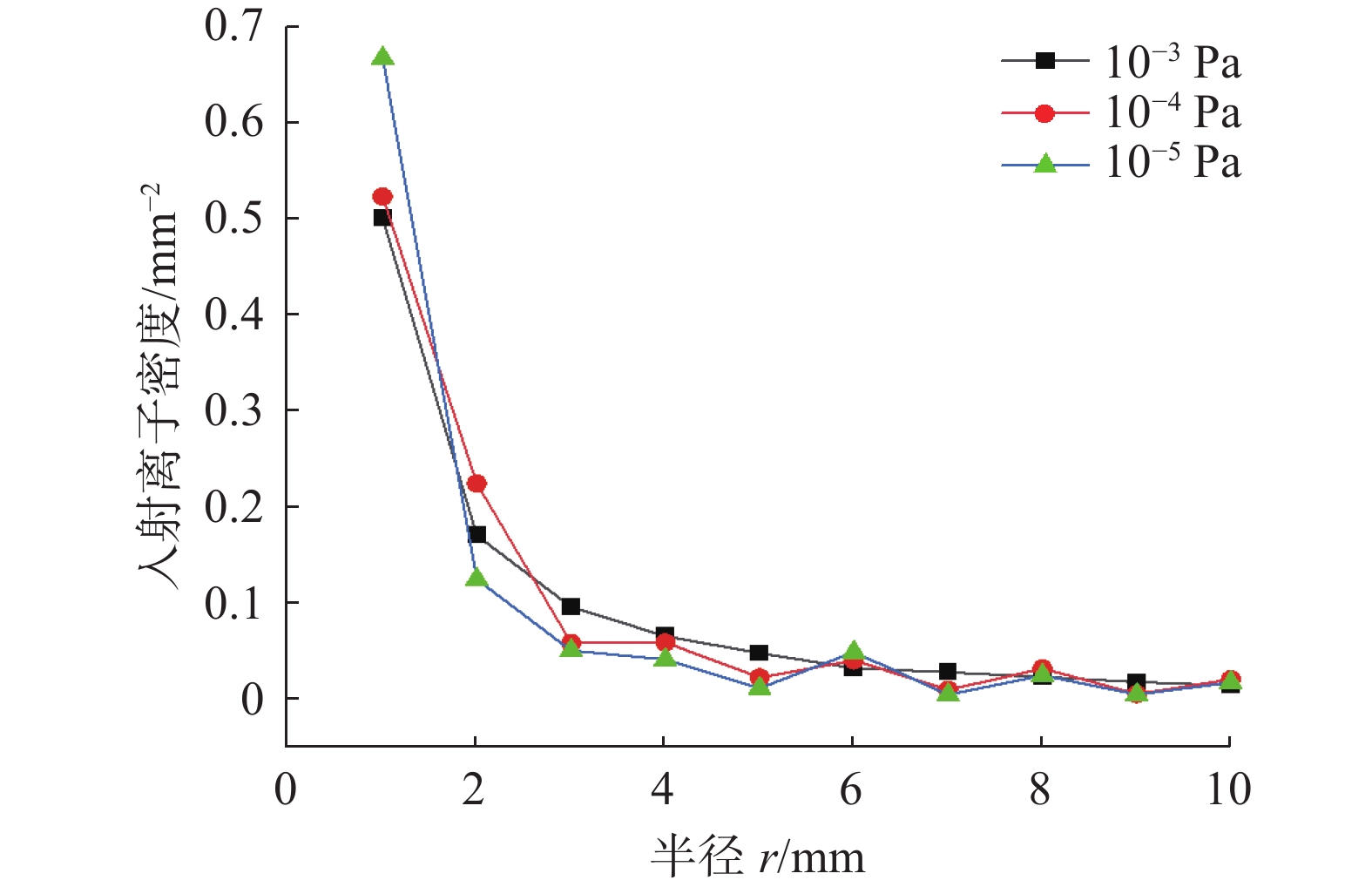
3.2.1   入射位置分布

通过picFoam得到的离子入射位置分布如图4所示，该分布与Ha等^[6]得到的结果是一致的。从图中可以得知，在溅射离子泵潘宁放电单元中，大部分的离子都在阳极筒的中轴线附近入射阴极，且入射离子密度随着半径的增大而减小。大部分的离子在中心处入射是溅射离子泵实际使用中阴极板被击穿的主要原因。

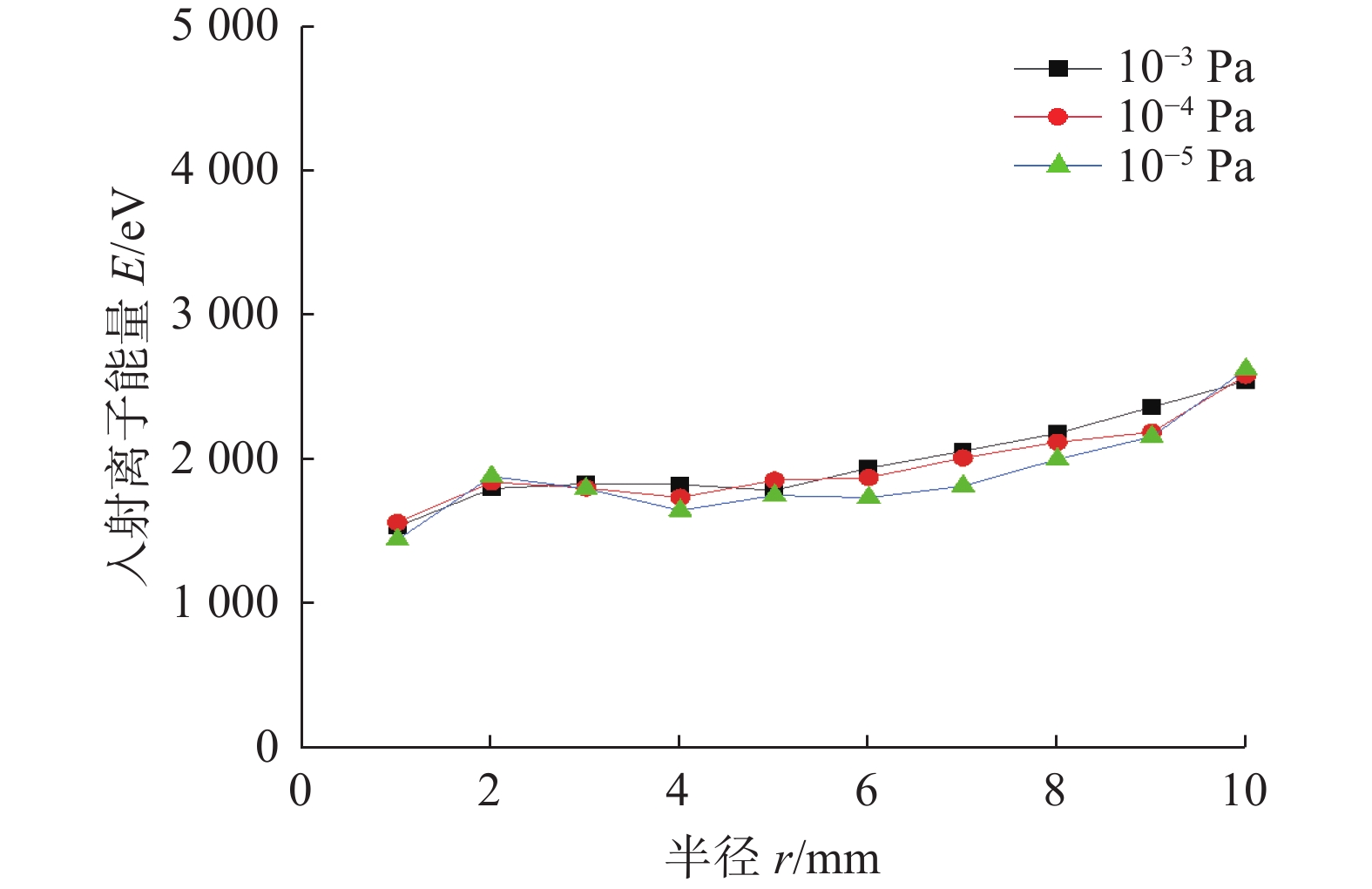
3.2.2   入射能量分布

不同半径下入射离子的平均能量分布如图5所示，从图中可以得知，离子入射能量随着半径的增大而增大，这与Ha等^[6]的结果相同，而根据Ha等的理论，这种能量的增大可能是在半径较大位置的边缘处，电场因靠近阳极板而变强，边缘附近离子的能量进而变大。

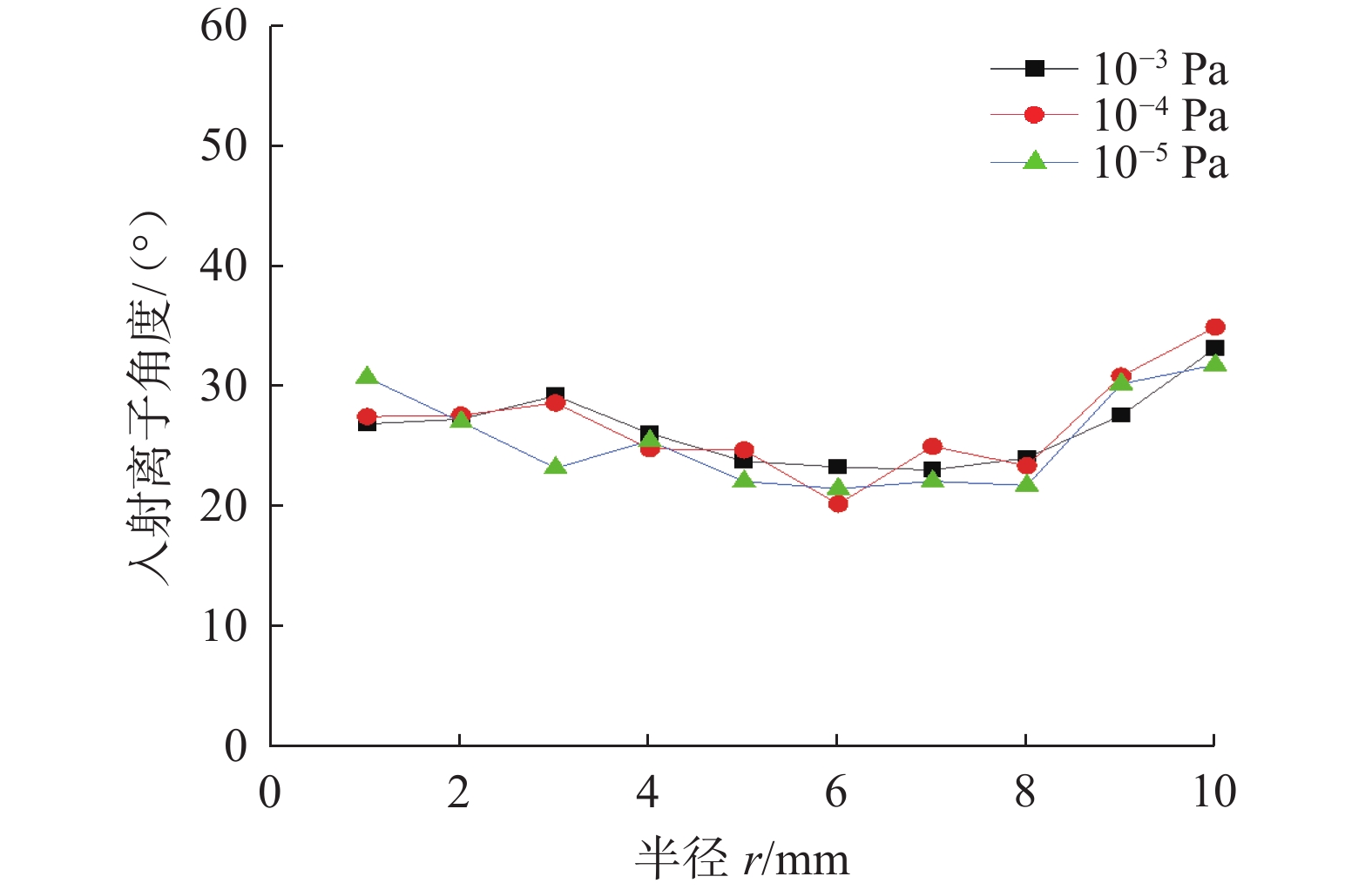
3.2.3   入射角度分布

离子的入射角度是离子的入射阴极板时，离子速度方向与阳极筒中轴线的夹角。不同半径下入射离子的平均角度分布如图6所示，离子的入射角度总体上呈先递减后递增的复杂形状，这种变化与离子的速度有关，在半径较小时离子的径向速度占主导，入射角度较大，而随着半径的增大径向速度也随之增大，轴向速度逐渐占主导，入射角度降低，但是在半径较大的边缘区域内，由于电场变强径向速度再次占主导，入射角度再次增大^[6]。从离子的入射角度分布可以得到，入射粒子的入射角度都较低，而根据田野^[21]的结论，入射角度越接近粒子入射时产生最大溅射产额的夹角$ {\theta _{\max }} $，溅射产额越大，而根据田野的结论，最大溅射产额夹角约为70°，这说明大部分的入射离子都以较低的效率溅射钛原子。

3.3   抽速计算

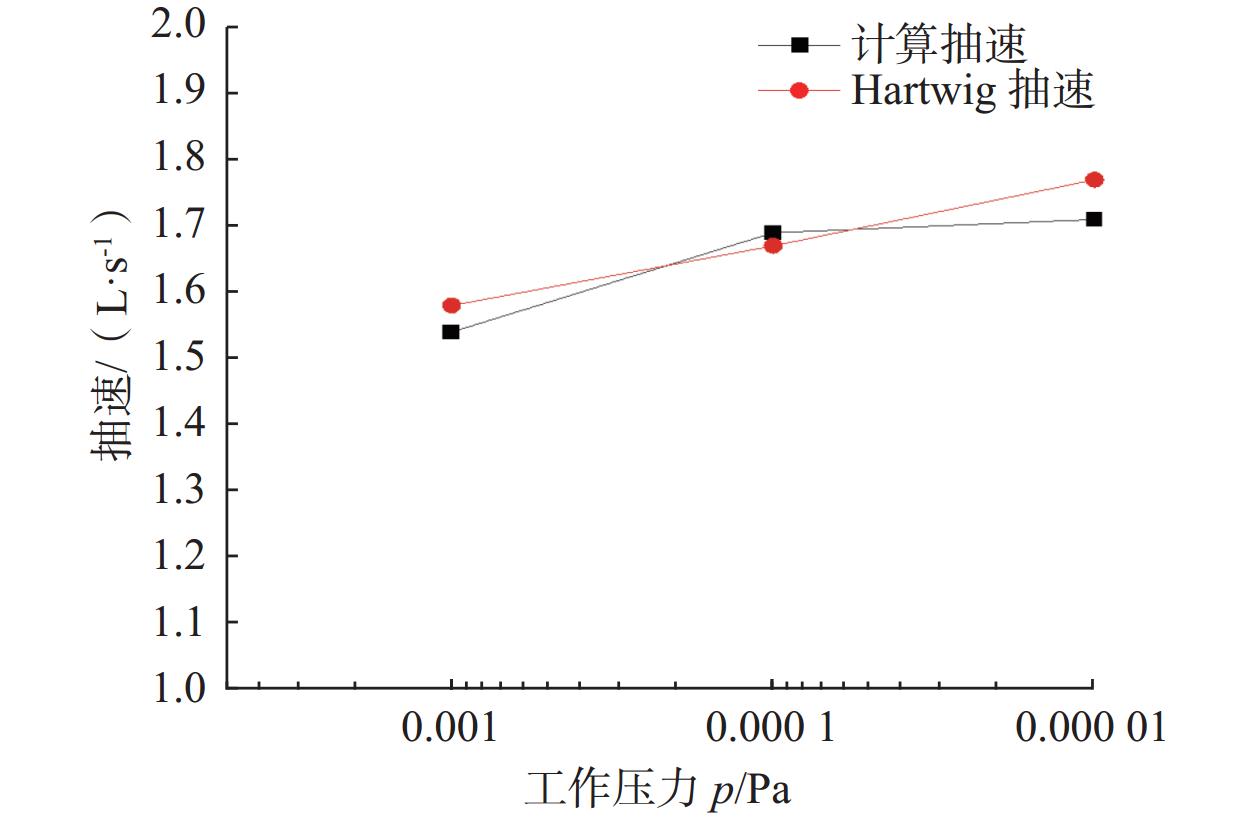
结合第 2 节内容，依据入射离子数以及离子的入射参数，对单个溅射离子泵潘宁放电单元的抽速展开计算，并将计算结果与Hartwig的理论结果^[2]作对比，对比结果如图7所示，计算结果与理论结果变化趋势相同，一致性良好。

图  7  不同工作压力下单个潘宁放电单元的抽速与Hartwig理论抽速对比

Figure  7.  Comparison of pumping speed of a single Penning discharge unit under different working pressures andHartwig's theoretical pumping speed

下载: 全尺寸图片 幻灯片

由图7可以发现，抽速随工作压力的变化出现了拐点。拐点在Hartwig的理论抽速计算中同样出现，在其理论中，拐点被认为是磁场与工作压力共同导致的，当放电空间中磁场保持不变时，存在一个可以获得最佳抽速的工作压力，称为过渡压力。在磁场条件不发生变化的前提下，当工作压力大于过渡压力时，抽速会随工作压力的减小而增大 ，当工作压力小于过渡压力时，抽速会随着工作压力的减小而减小^[2]。

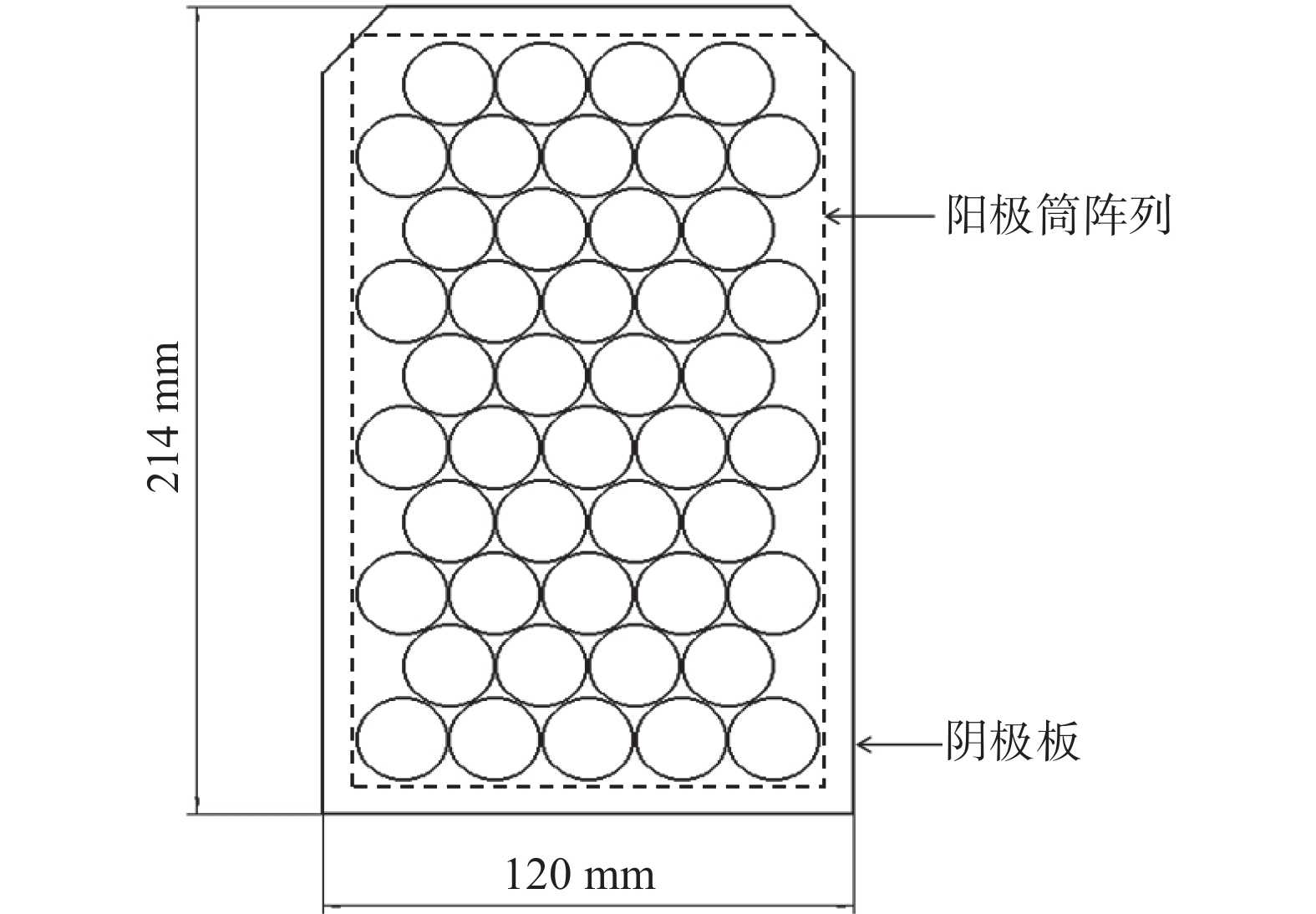
为了进一步探究抽速计算结果的精准度，采用与刘亦兵等^[22]研制的LH-300型冷阴极泵相似的阳极筒排列方式对溅射离子泵整体抽速进行计算。

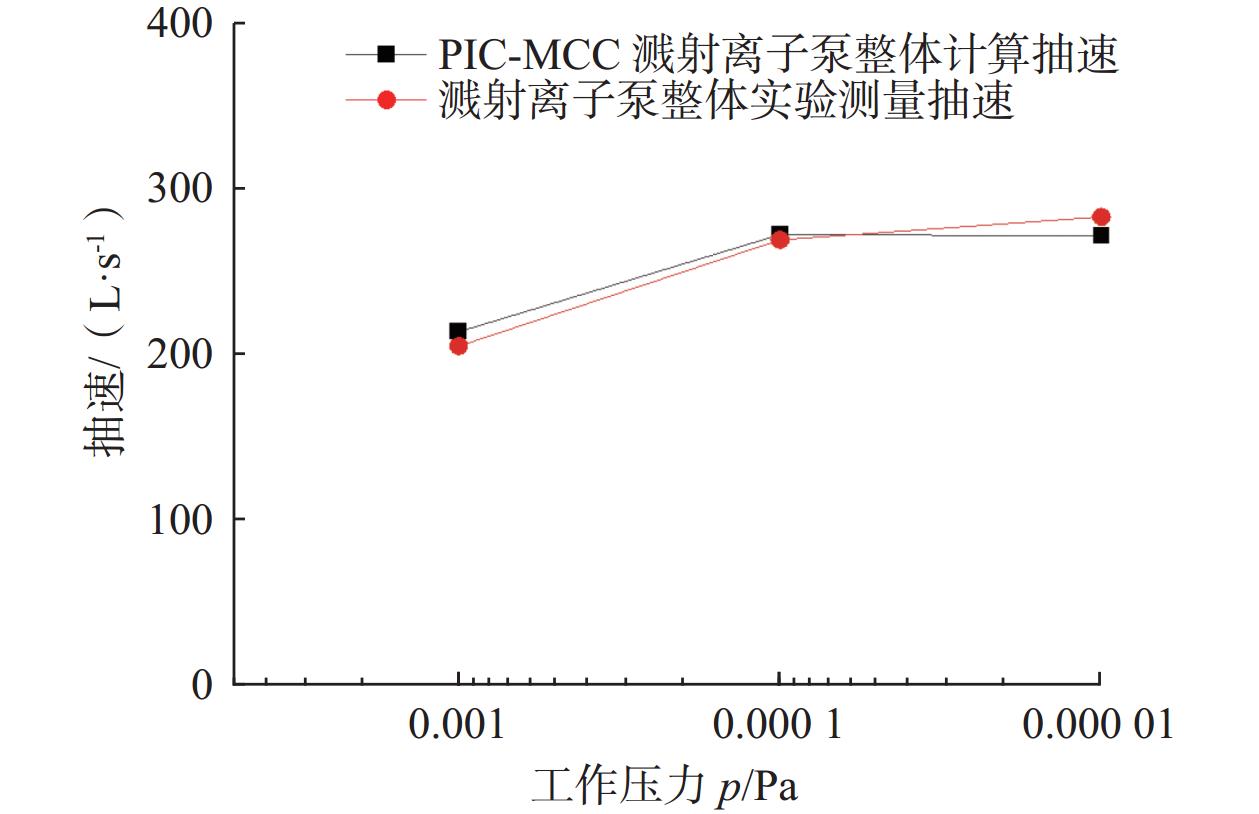
单个抽气单元的结构与参数如图8所示，在溅射离子泵内部存在8个类似的抽气单元。确定阳极筒排列方式与抽气单元参数后，对单个潘宁放电单元抽速进行修正，并结合抽气单元参数对溅射离子泵整体抽速进行计算，溅射离子泵的计算抽速与实验结果对比如图9所示，计算抽速与实验测量抽速的相对误差为4.4%。

图  8  单个抽气单元内部的阳极筒排列方式

Figure  8.  The arrangement of anode cylinders inside a single exhaust unit

下载: 全尺寸图片 幻灯片

虽然理论计算值与实验测量值存在一定差异，但抽速的计算结果可以反映溅射离子泵的抽气特性，这种通过模拟仿真计算溅射离子泵潘宁放电单元抽速的方法可以作为设计或改进溅射离子泵性能的参考依据。

图  9  不同工作压力下溅射离子泵整体抽速对比

Figure  9.  Comparison of overall pumping speed of sputtering ion pump under different working pressures

下载: 全尺寸图片 幻灯片

4.   结论

采用PIC-MCC方法对溅射离子泵单个潘宁放电单元进行模拟，通过模拟获得单个潘宁放电单元的离子电流（入射离子数）、入射能量、入射角度等相关参数，并通过计算得到单个潘宁放电单元的抽速。仿真得到的离子电流与实验测试变化趋势一致，将计算得到的抽速与现有实验测量值对比，相对误差不超过5%。

对不同工作压力下的离子入射参数以及抽速进行了分析。在10⁻⁵~10⁻³ Pa压力下，工作压力的变化对放电空间内电子的运动规律以及离子的入射参数影响较小，离子的入射位置分布、入射能量分布、入射角度分布在不同工作压力下变化趋势相似。

尽管本文对溅射离子泵单个潘宁放电单元抽速计算值与理论值对比一致性好，结果可靠，但是还需要进一步的实验验证。且当前模拟仅局限于单个潘宁放电单元，为了获得更加精准的抽速，在后续研究工作中，有必要对计算方法予以进一步优化。