Application and Progress of Calibration Technology of High-precision Thrust Stand
-
摘要:
微推进器在航天器姿态控制、轨道维持和阻力补偿中具有广泛应用,而应用的前提是对其推力的直接测量。微推进器产生的推力通常为mN级或更低,并且具有较低的推重比,需要使用推力架对其推力性能进行高精度测量和评估。推力架作为测量仪器,在进行推力测量前需要标定。标定过程主要是通过将精确可知的力或冲量作用在推力架上,记录响应情况,得到推力架响应与作用力或冲量之间的对应关系。随着航天技术的发展,一些高精度空间任务对推进器推力范围、分辨率和稳定性等参数的要求不断提高,同时对推力架测量能力以及相应标定技术的稳定性、精确性和可操控性提出了更高的要求。根据标定方法的不同进行分类,综述了近年来高精度推力架标定技术的研究进展。通过介绍和分析重力法、冲击力法、静电力法、电磁力法和气体分子作用力法等标定方法的原理、装置及应用情况,评述和总结了不同标定方法的适用条件和特点,并对高精度推力架标定技术的未来发展趋势进行了展望。
Abstract:Microthrusters are widely used in spacecraft attitude control, orbit maintenance and drag compensation, and the direct measurement of their thrust is the premise of their application. The thrust generated by microthrusters is usually at or below the mN level and has a low thrust-to-weight ratio. The thrust stand is often used to measure and evaluate its thrust performance with high precision. As a measuring instrument, the thrust stand needs to be calibrated before the thrust measurement. The calibration process is mainly to obtain the corresponding relationship between the response of the thrust stand and the force or impulse by applying the accurately known force or impulse on the thrust stand and recording its response. With the development of space technology, some high-precision space missions have increasing requirements for thrust range, resolution, stability and other parameters of thruster. At the same time, higher requirements are also put forward for the measurement capability of the thrust stand and the stability, accuracy and controllability of the corresponding calibration technology. The different calibration methods and the research progress of high-precision thrust stand calibration technology in recent years are classified. The principle, device and application of calibration methods such as gravity method, impact force method, electrostatic force method, electromagnetic force method and gas molecular force method are introduced and analyzed. The application conditions and characteristics of different calibration methods are reviewed and summarized, and the future development trend of high-precision thrust stand calibration technology is prospected.
-
Keywords:
- micro-thrust measurement /
- thrust stand /
- micro-thruster /
- calibration technique
-
0. 引言
随着航天技术的高速发展和航天任务的复杂化、多样化,人类对航天器探测系统的精度、稳定度要求越来越高。相较于地面环境,空间环境的高微重力水平,超低扰动特性可使航天器实现高精度高稳定度运动,从而为各类探测仪器提供精确稳定的工作状态。因此,近年来相继提出了天基地球重力场测量[1]、天基引力波探测[2]等基于卫星平台的空间科学任务。然而,在空间环境中,卫星平台仍受到太阳光压、宇宙射线等外部环境扰动和卫星结构振动、姿态调节、卫星内部移动部件等自身扰动的影响,通常需要使用无拖曳控制技术维持卫星平台的超精超稳飞行状态,以满足各类星载高精度仪器的要求[3]。微推进器是无拖曳控制系统的重要执行机构,用于产生推力补偿航天器受到的非保守力[4]。表1给出了几个典型的空间科学任务及其推进系统要求,可以看出应用于空间科学实验的高精度微推进器的推力通常为微牛级到毫牛级,推力分辨率可达亚微牛级。
推力的直接测量是微推进器应用的前提。由于微推进器产生的推力很小,推重比低,常规微弱力测量设备无法满足其测试需求,需要研发推力架对其推力性能进行准确的测量和评估。国内外主要应用的推力架结构有悬摆结构、倒摆结构、扭摆结构和天平结构等。由于工作机理的差异,每种推力架构型都有其优点和局限性[11-13],应用范围也略有不同,典型推力架结构及性能如表2所列。
表 2 典型推力架结构特点及应用Table 2. Structural characteristics and applications of typical thrust stand推力架类型 特点 研究机构 性能参数 应用 悬摆结构 回复力为重力,稳定,无温漂;非线性,灵敏度和极限承载质量难以兼得。 The French Aerospace Lab[14] 测量范围:0.1~1000 μN
分辨率<0.1 μNGAIA任务冷气和FEEP
推力测试倒摆结构 结构紧凑,灵敏度高,承重大;结构不稳定,需要主动控制,易受温度影响。 MIT Space Propulsion Lab[15] 测量范围:0~23 mN
不确定度:±0.5 mN用于卫星轨道控制Hall
推力器推力测试扭摆结构 测量范围宽,测量精度不受重力影响,回复力线性;尺寸较大,需要配平,易受温度影响。 NASA Goddard Space Flight Center[16] 测量范围:1~100 μN
分辨率0.1 μNLISA任务胶体和FEEP
推力测试天平结构 易于校准,可以测量推进剂质量损失;需要配平,不适用于小推重比测量。 东京大学[17] 推力测量范围:0~1600 μN
冲量测量范围:0~1000 μN·s
误差<5%ALOS-3卫星PPT
推力测试在使用推力架对微推进器进行推力测量前,需要对其参数进行精确的标定。标定过程通常由微弱力产生装置对推力架施加匹配其量程的已知力或冲量,进而测量推力架的响应。通过标定,可以获得摆臂偏转或传感器输出与推力或冲量之间的关系,同时获得推力架的精度、分辨率和可重复性等关键参数。此外,通过比较摆架响应与理论预期间的差别,可以降低系统误差[18]。
为了满足高精度微推进器的推力测试需求,推力架的精度需要达到微牛级甚至亚微牛级。在该范围内,力值和冲量施加的稳定性和精度受各种干扰因素的影响很大,对标定装置的稳定性、精确性和可操控性也提出较高的要求。本文对常用的推力架标定技术的原理、操作过程、技术特点等方面进行了综述分析,对这些方法在高精度空间科学任务中的应用及前景进行了回顾和展望。
1. 标定技术原理与应用
根据力或冲量施加时推力架与外部装置有无接触,可将标定技术分为接触式和非接触式两类。
1.1 接触式标定技术
通过与推力架的接触施加力或冲量,该类方法通常具有原理简单、易于实现的优势。常用的接触式标定技术可分为重力法和冲击力法。
1.1.1 重力标定方法
重力标定方法是利用物体在地球引力场中受到的重力作用对推力架施加已知力值或冲量的方法。由于在地球同一地点的重力加速度基本保持恒定,因而重力法可以直接溯源到基本物理量,无须再校准,因此重力法具备原理清晰、可信度高的特点,也是在推力架标定中最常用的一种方法。重力方向竖直向下,但根据摆架结构及布置方式的不同,竖直向下的力可能无法实现标定。解决方案有两种:一种是利用绳和滑轮的组合改变力的方向,即绳系质量—滑轮结构;另一种是使用力矩等效结构,在摆架上添加杆或其他结构,使重力作用对摆架转动中心产生一定的力矩作用。
(1)绳系质量—滑轮结构
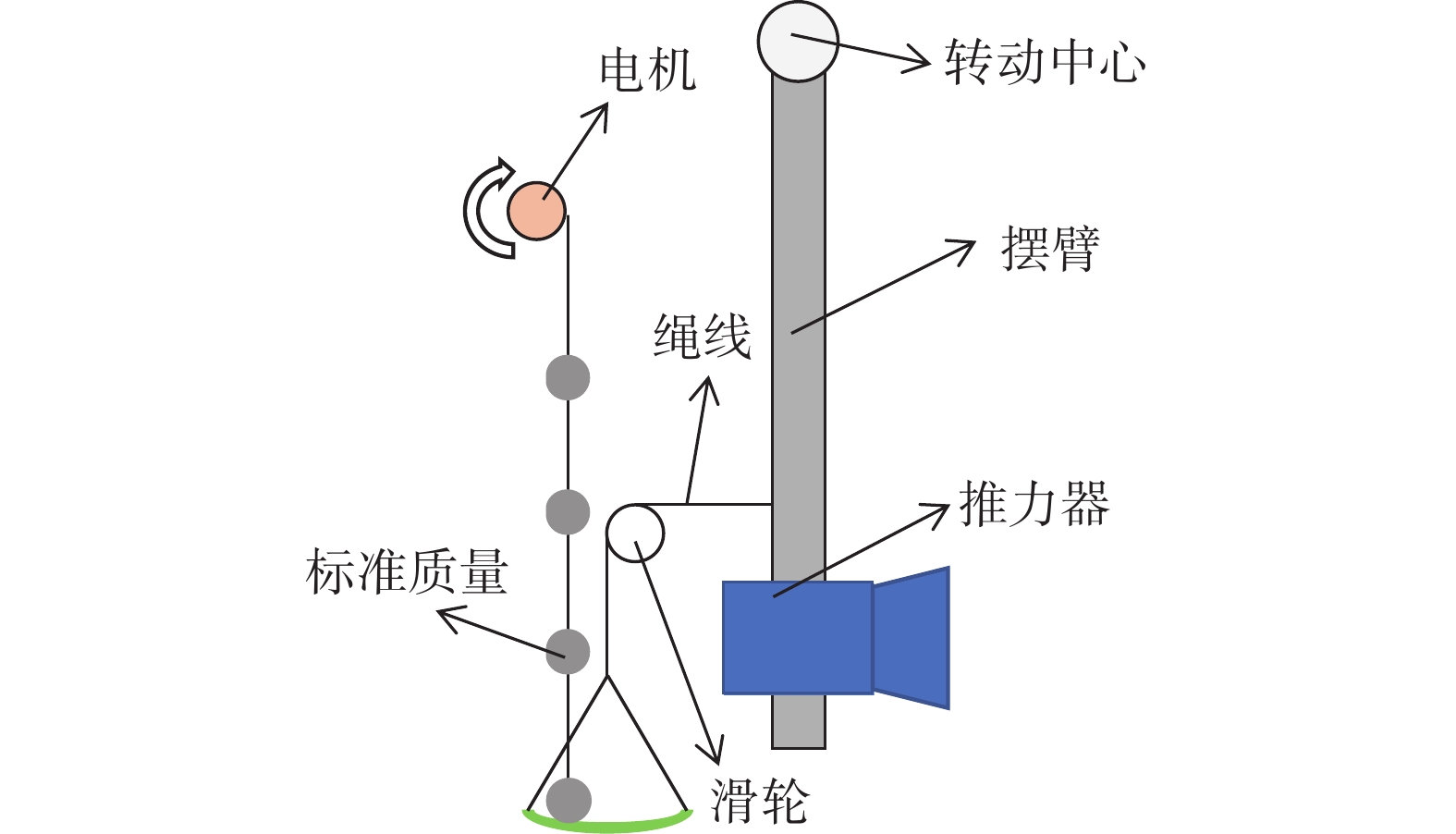
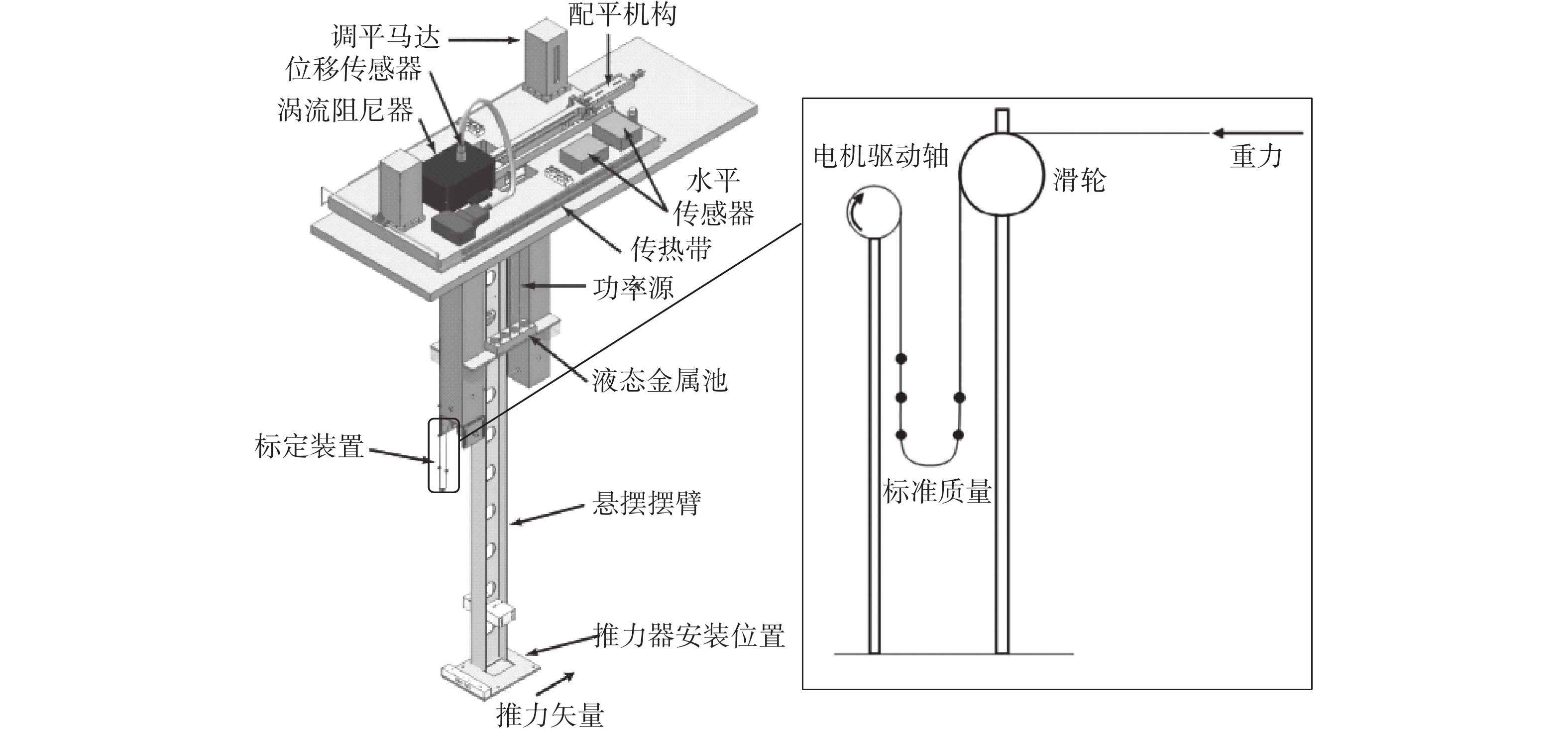
绳系质量—滑轮装置通常采用砝码或其他标准质量物体和滑轮组件,利用标准质量的重力提供标定力。装置结构通常如图1所示,利用电机驱动加卸载标准质量,通过滑轮组件将重力稳定地转换为推力架测力方向的标定力[19]。典型应用实例如图2所示[20],Polzin等使用绳系质量—滑轮装置,通过电机驱动加卸载五个标准质量砝码,利用低摩擦滑轮将砝码重力转换为标定力,实现了对悬摆推力架VAHPER的标定。
绳系质量—滑轮装置原理清晰易于实现,无须再校准,通过绳和滑轮的组合可改变力的施加方向,适用于不同类型推力架的标定,已在各类毫牛级精度推力架的标定中得到了广泛应用。然而,绳系质量—滑轮装置中滑轮摩擦和绳线弹性的误差无法避免且难以评估,利用该装置产生微牛级标定力时将产生较大的不确定度。
(2)力矩等效结构
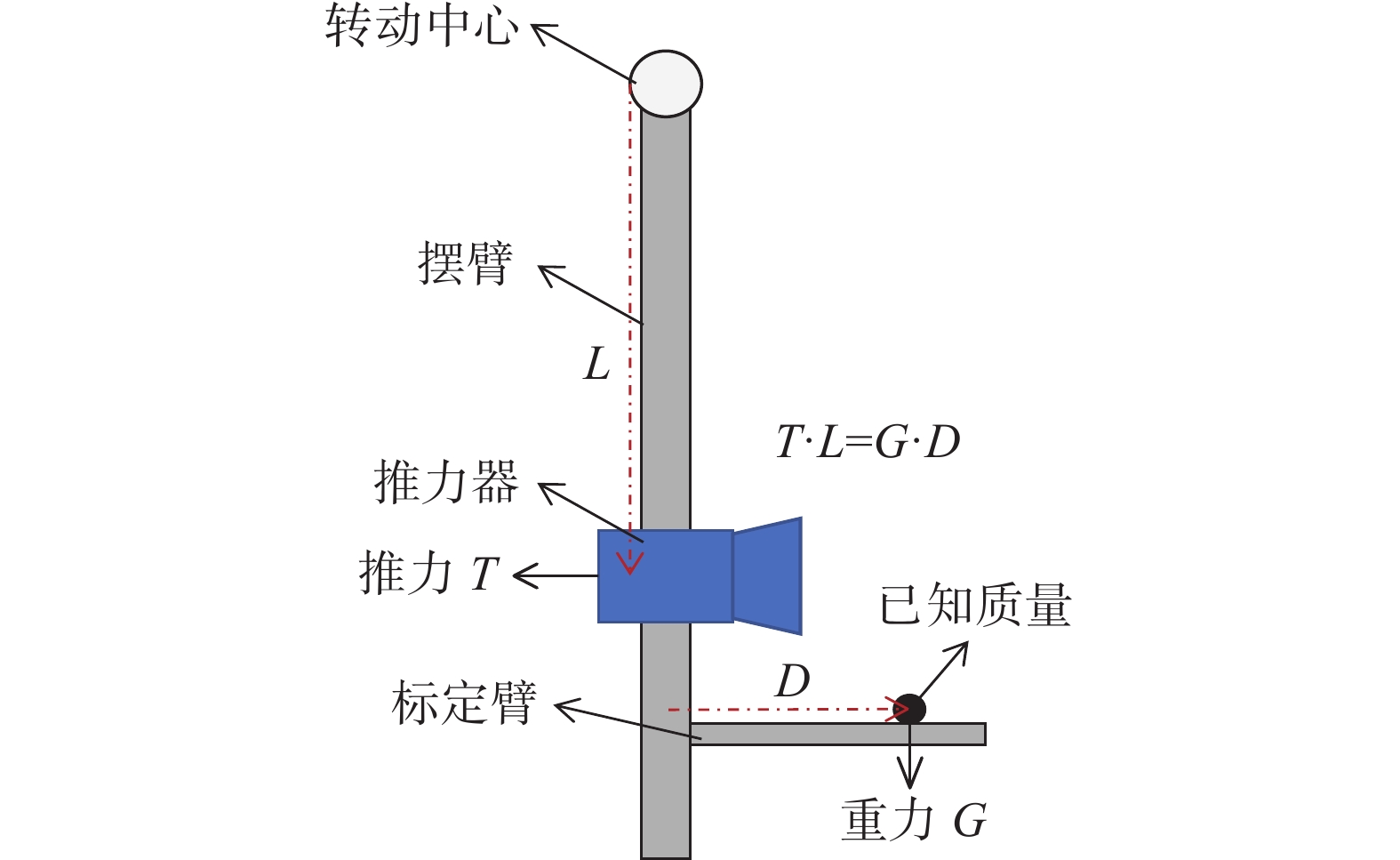
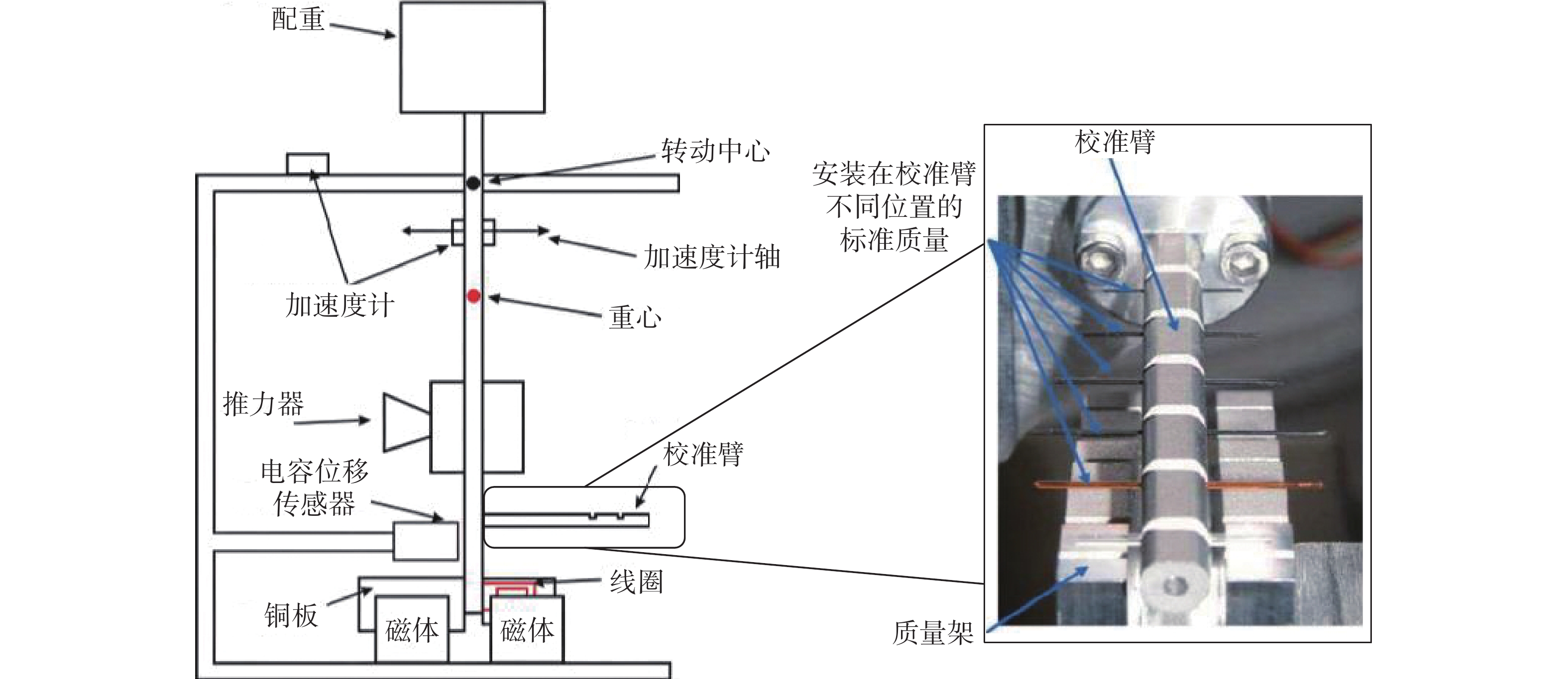
力矩等效装置通过在推力架特定位置加载已知质量产生与推力作用等效的力矩,从而获得推力架在等效推力作用下的响应。装置结构如图3所示,在摆臂或外延的标定臂上的特定位置加载已知质量的物体,对推力架转动中心产生与推力作用等效的力矩。根据作用力臂可推算出重力与推力的等效关系,进而可获得推力架在等效推力作用下的响应[21]。典型应用实例如图4所示[14],Jarrige等通过在单摆校准臂上的不同位置加载6.20~194.70 mg的标准质量,产生7.33~1016.20 μN的等效标定力。标定过程的误差主要来自于标准质量测量误差,约为0.5%。
力矩等效装置规避了绳线弹性和摩擦等不确定因素的影响,可以产生宽范围、高精度的标准力,但该装置的应用会增加推力架结构的复杂度,且力矩等效过程会引入额外的不确定度和位置测量误差。
1.1.2 冲击力标定方法
冲击力标定方法利用物体与摆臂碰撞时产生的冲击作用进行推力架标定,可提供较宽范围的脉冲冲量,但无法提供稳态标定力。冲击力法根据作用方式的不同,又可细分为力锤法、冲击摆法和落球法。
(1)力锤法
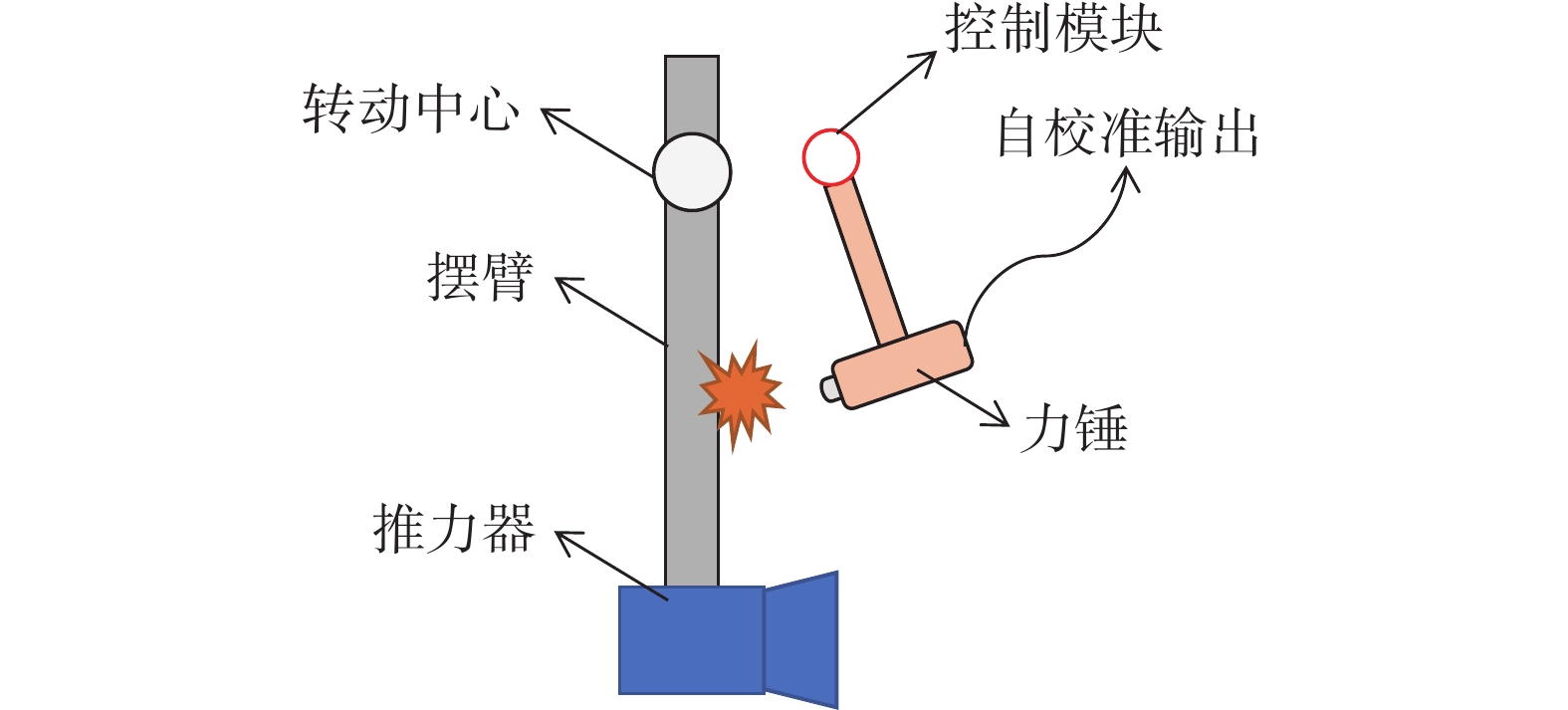
力锤法采用高频响的力锤敲击摆臂的特定位置,对推力架施加微冲量。力锤在计量领域具有广泛应用,其本身是力传感器,将力信号转换为电信号输出,通过校准可获得两者间的转换关系。力锤标定装置如图5所示,力锤敲击摆臂时会产生电信号输出,由此可反推出力信号,然后对时间积分即可得到施加的脉冲冲量大小。
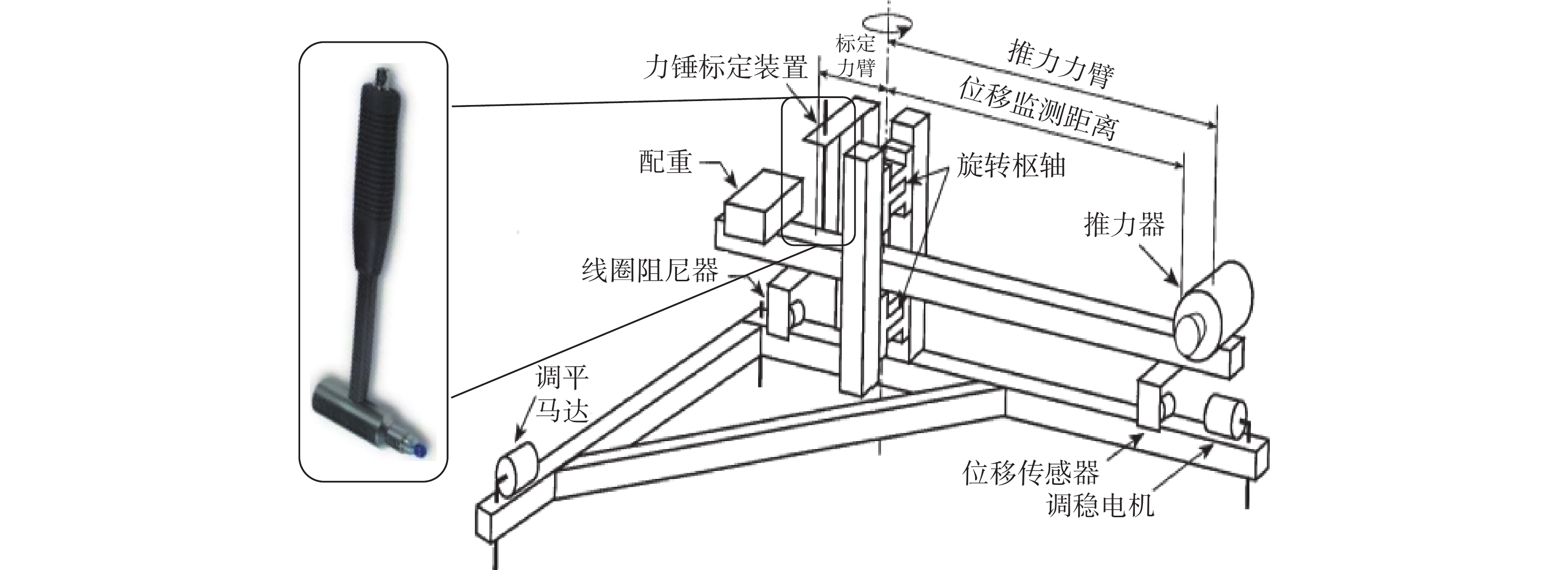
力锤法可产生μN·s~N·s范围的微冲量。通过对力锤的伺服控制,该方法可达到较高的微冲量输出精度,常用于对采用扭摆结构的推力架的标定。Ziemer等[22]使用力锤法完成了对如图6所示扭转式推力架的标定。通过控制电磁铁的旋转角度改变冲击锤装置的下落位置,可产生220~650 μN·s的微冲量。在使用力锤装置进行推力架标定前,通常需要对力锤冲击力敏的灵敏度进行校准。Pancotti等[23]使用软尖端加速度计对商用力锤(型号:PCB 086C02)进行了多次校准,测得其冲击力敏灵敏度为12.50 mV/N,误差<0.5%。进而通过伺服控制系统控制力锤对推力架施加了0.5~600 mN·s的微冲量。在10~20 mN·s的冲量范围内,力锤输出非线性误差仅为0.31%。
(2)冲击摆法
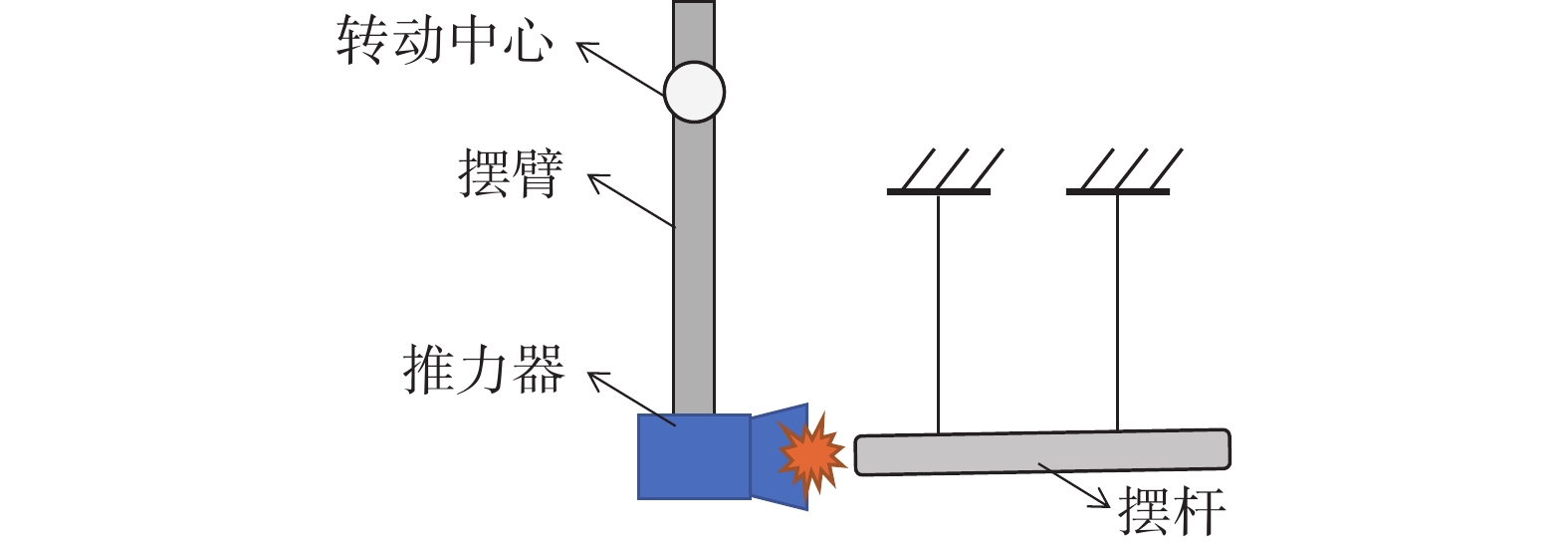
冲击摆法采用已知质量的摆撞击推力架的特定位置,进而完成冲量的施加。冲击摆装置原理如图7所示,用一个已知重量的摆杆撞击安装于摆架上的推力器中心位置,以模拟真实的推力器冲量输出。通过测量摆杆撞击前后的速度或加速度变化,进而计算摆杆传递给测量台架的冲量输出。
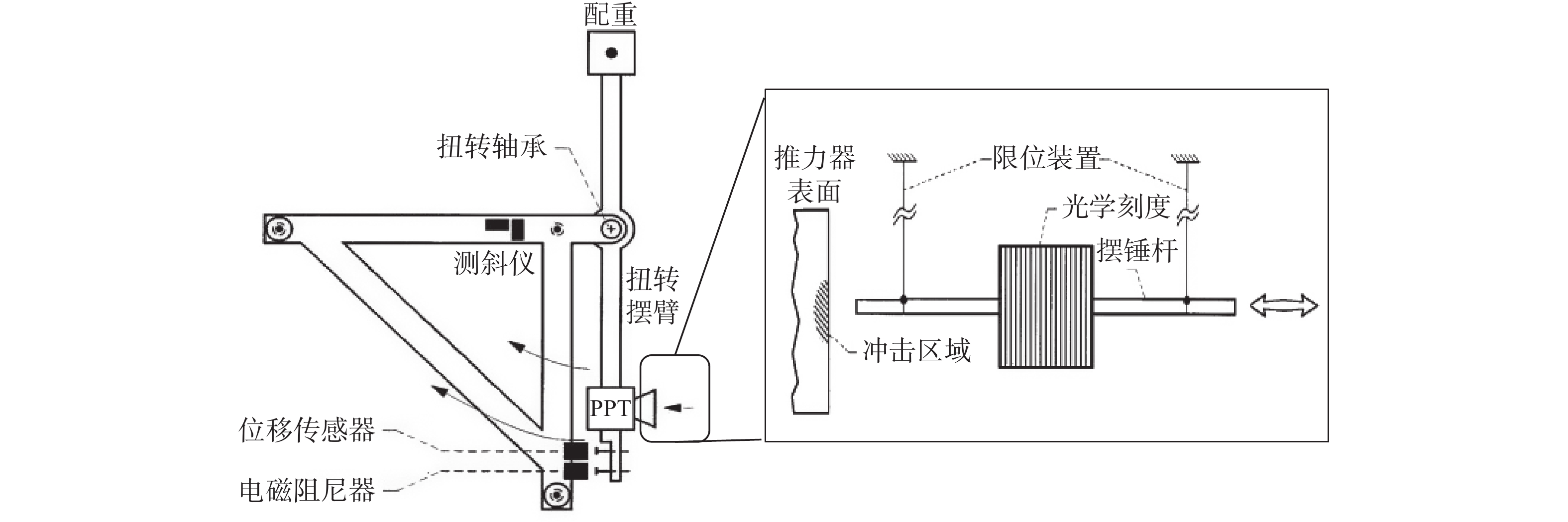
冲击摆装置的优点是输出冲量可直接溯源到基本物理量,缺点是装置较为复杂,响应较慢。典型应用如图8所示[24],Haag等使用冲击摆装置产生85~412 μN·s的冲量,完成了对扭摆结构推力架的标定。其中,悬杆的质量通过天平称量获得,悬杆撞击前后的速度变化使用光栅、光电管和光源监测。
(3)落球法
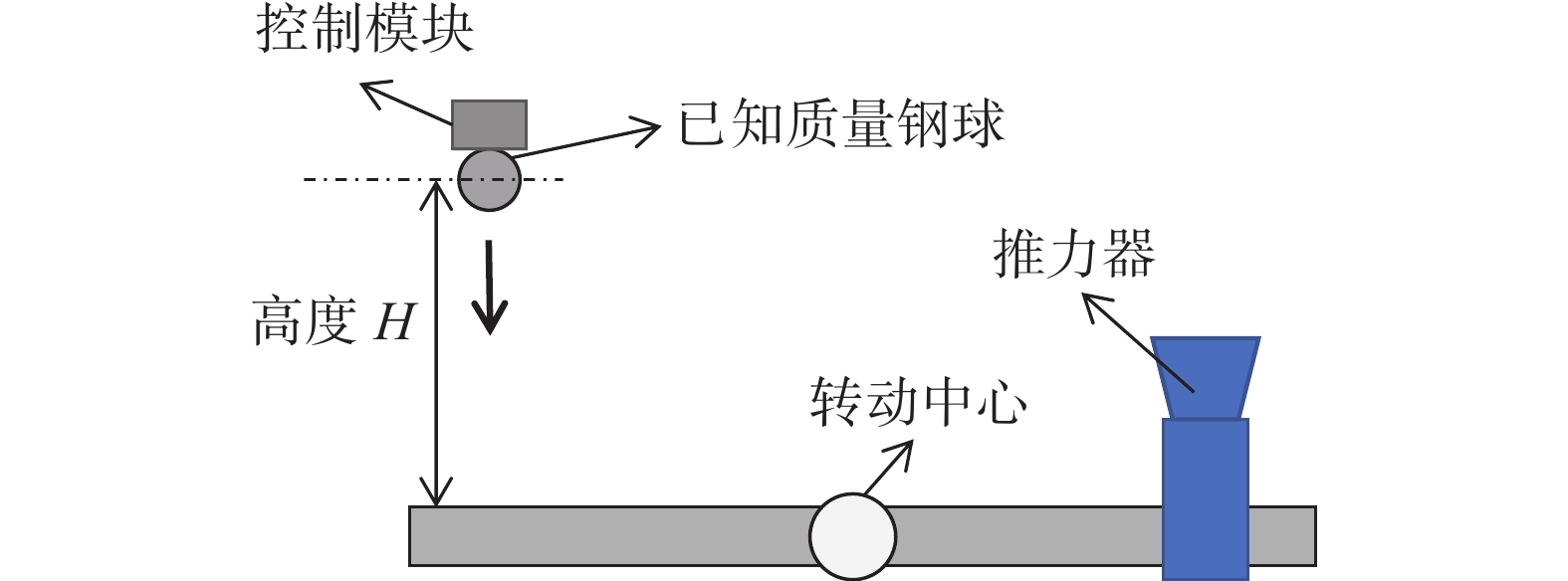
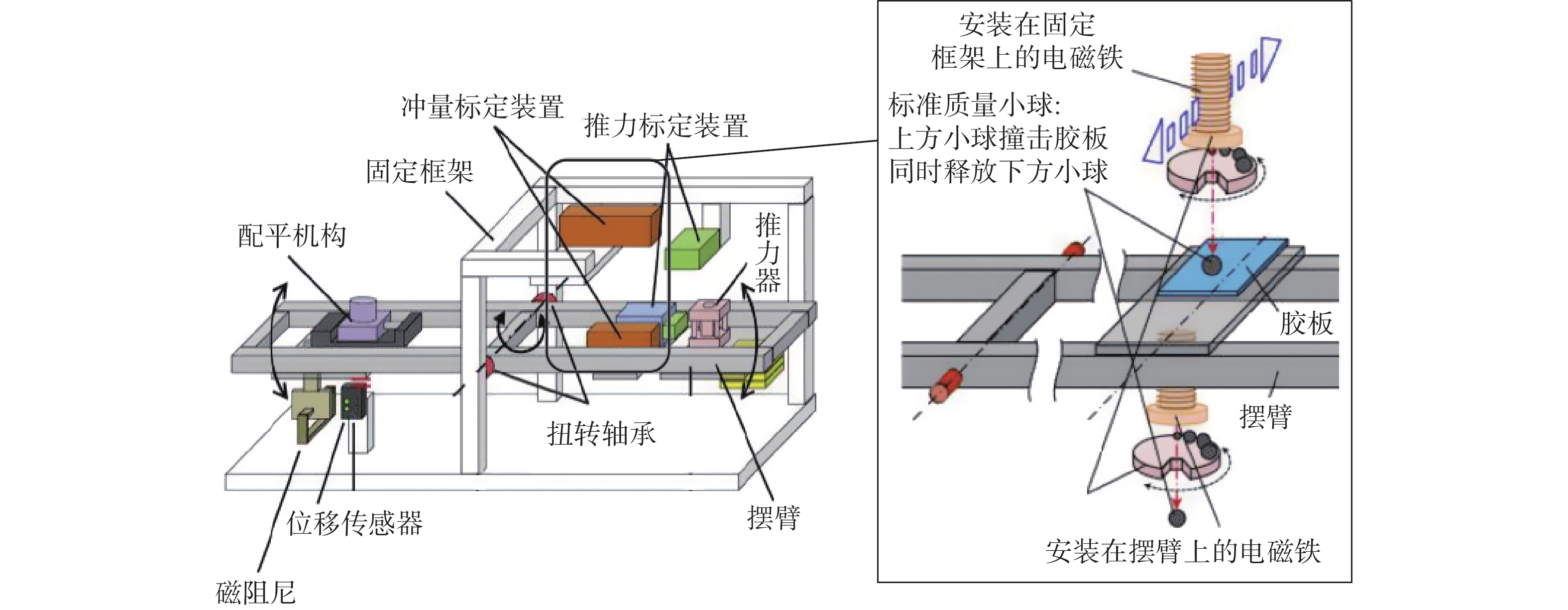
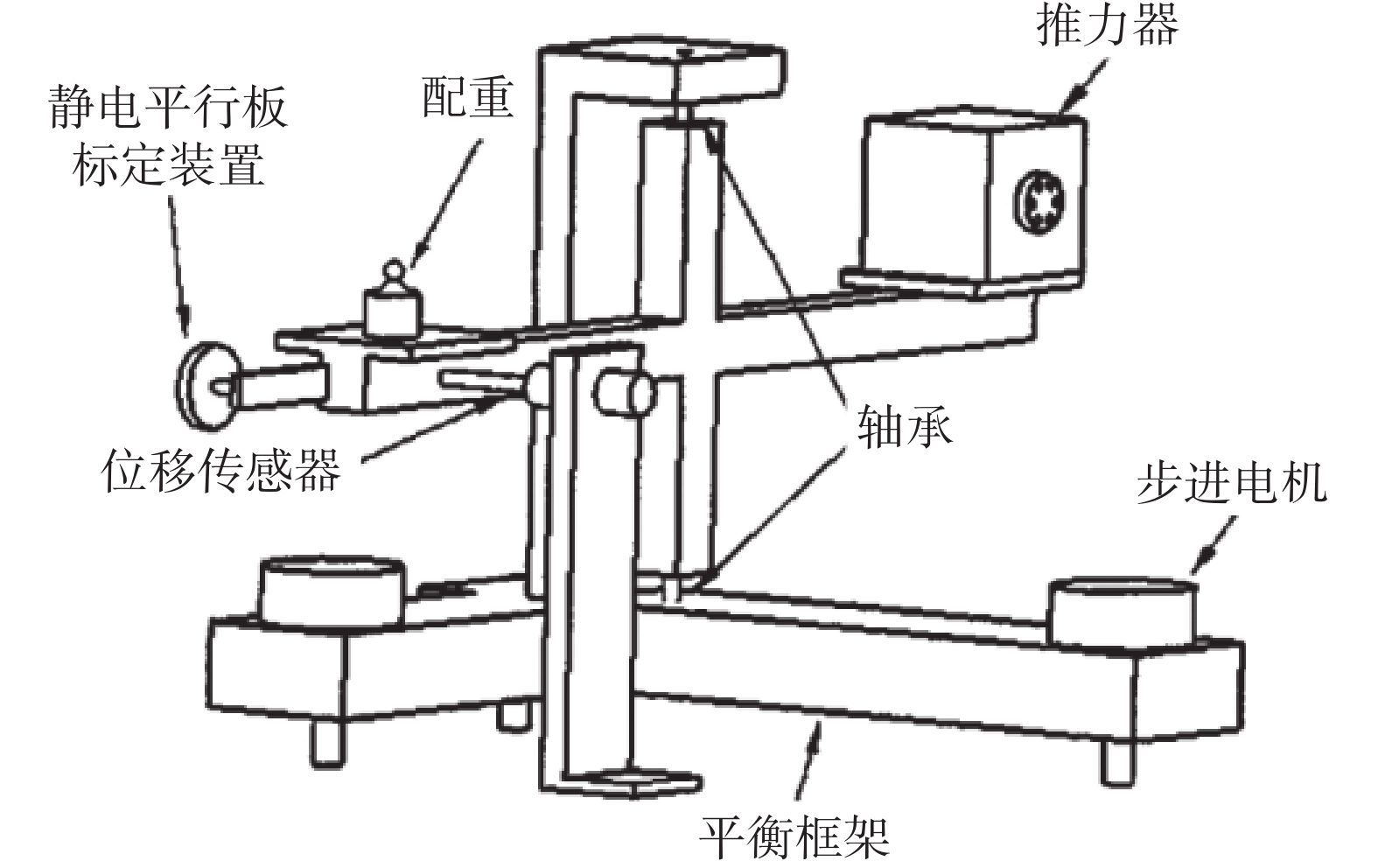
落球法冲量施加装置如图9所示,从已知高度释放一个已知质量的自由下落钢球,利用球体的自由落体运动产生的冲击完成对推力架冲量的施加。冲量可通过测量钢球撞击摆架前后的速度变化计算得到。也可在下方摆臂上放置球体吸附装置,使钢球与摆臂发生完全非弹性碰撞,进而利用钢球下落高度计算输出冲量。典型的应用例如图10所示[17],东京大学Yoshikawa等在对天平结构推力架的标定中,使用落球法装置产生270~1040 μN·s的微冲量。为了防止钢球被摆臂吸附后引起的质量变化进而产生的阶跃响应,在撞击的同时,从钢球落点下方的电磁铁释放出质量相同的钢球。
落球法原理简单,可直接溯源到基本物理量,但装置较为复杂,且仅能产生与重力方向相同的冲量,应用范围受限。
1.2 非接触式标定技术
非接触式标定技术在力值或冲量施加时,施力组件与推力架没有直接接触。相比于接触式标定技术,该方法避免了装置线路对推力架力学特性的影响,同时装置更易于控制。根据作用原理的不同,非接触式标定技术主要包括静电力法、电磁力法、气体动力学法等。
1.2.1 静电力标定方法
静电力标定方法利用通电极板间的静电力作用,对推力架实现力值施加。根据装置结构的不同,常用的静电力标定装置主要包括平行电极板和静电梳等。
(1) 平行电极板
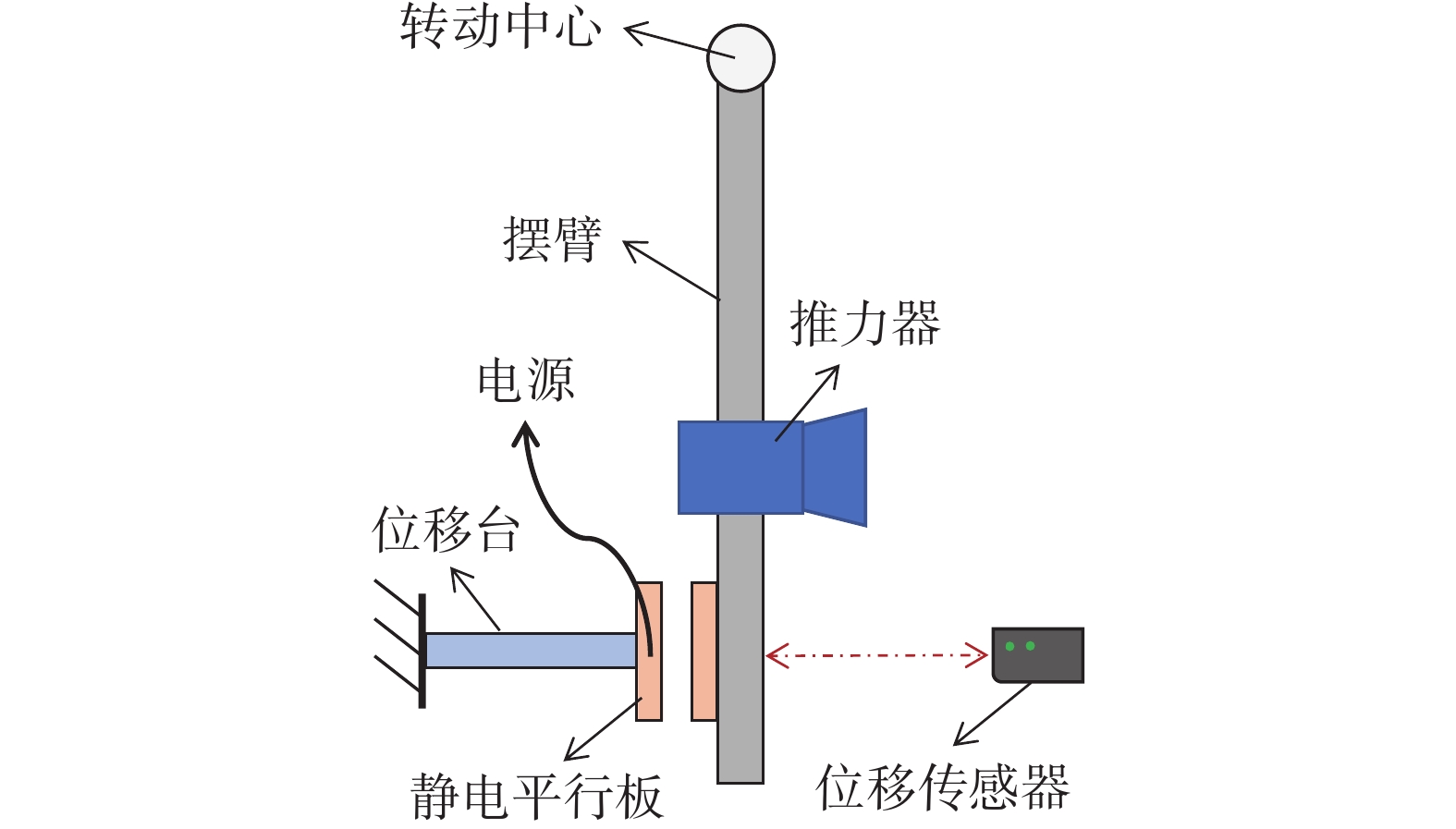
平行电极板装置利用通电时两电极板之间产生的静电排斥力对摆架施加作用力。在使用平行电极板装置进行推力架标定时,将一个电极板安装在摆臂上,将另一电极板安装在固定部件上[25],如图11所示。
理想状态下,两电极板之间的静电力可表示为:
$$ {F}_{静电}=\frac{1}{2}\varepsilon A\frac{{U}^{2}}{{x}^{2}} $$ (1) 式中:$ \varepsilon $为介电常数;U为电压;x为间距;A为电极面积。在平行电极板装置实际应用时,由于边缘效应等非理想因素影响,通常需要使用高精度天平对静电力进行再校准。平行电极板装置的典型应用如图12所示[26],Gamero-Castano等使用一组直径分别为5.08 cm和1.90 cm,间隙为1.10 mm的平行电极板,通过调节极板电压,产生了10~50 μN的静电力,完成了对μN精度扭摆的标定。
理论上平行电极板装置通过调节极板电压可产生高精度连续静电力值输出,但在实际应用中具有较大的不确定度。由式(1)可知,该标定方法的误差来源主要包括电压U、电极面积A和极板间距x的测量误差。其中电压U和极板面积A的测量可达到较高的精度,而间距x在标准力施加过程中,会随摆臂运动发生改变。假设x为5 mm,当Δx为0.5 mm时,就会引起静电力输出20%的误差。
天津大学郑叶龙团队使用平行板电容器作为标定装置,通过电容梯度建立起静电力与电压的关系:
$$ {F}_{静电}=\frac{1}{2}{U}^{2}\frac{\mathrm{d}C}{\mathrm{d}x} $$ (2) 式中:U为电压;C为电容。将一块电容板固定在摆臂上,通过给极板施加电压,对推力架产生静电标定力。由于电容器电容与板间间距呈线性变化,电容梯度基本不变,因此可以减小极板间距变化对静电力的影响。通过对极板施加0~300 V的电压,装置可产生1~279 μN的静电力输出,不确定度为0.18%[27]。该装置输出静电力可溯源至基础物理量,无须再校准,缺陷在于静电力的非线性以及电容梯度测量系统较为复杂。
(2)静电梳
静电梳装置结构如图13所示,由两组互锁的非接触式梳齿形电极板组成,通过对极板施加电压来产生静电力。两组梳齿形电极板间产生的静电力为[28]:
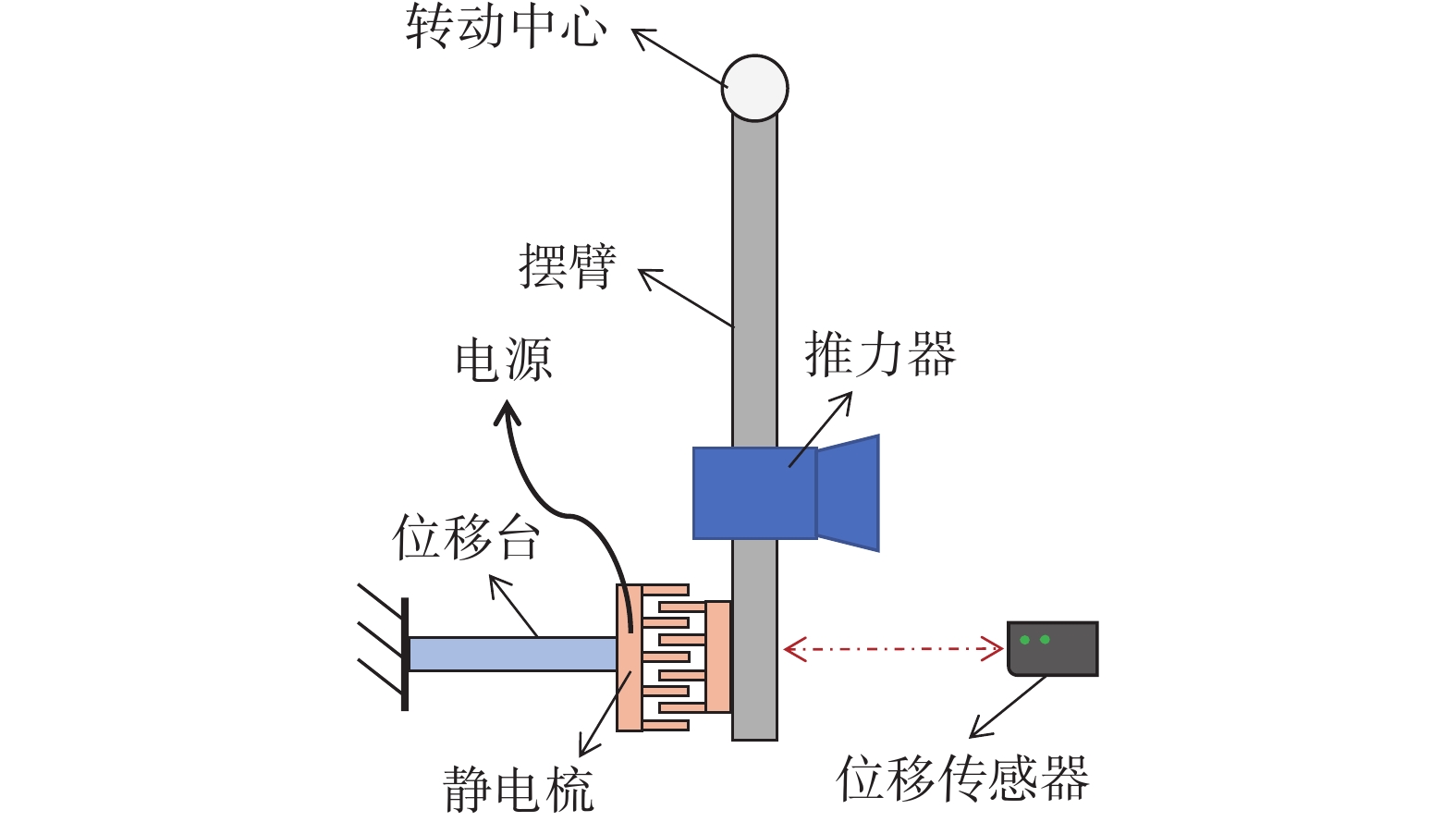
$$ {F}_{静电}=\frac{N{\varepsilon }_{0}t}{g}{V}^{2} $$ (3) 式中:N为梳齿对的个数;$ {\varepsilon }_{0} $为介电常数;t为梳齿电极板厚度;g为梳齿间距;V为两静电梳之间的电势差。在使用静电梳装置进行摆架标定时,为避免线路对推力架的影响,通常将接地的一组梳齿形电极板安装在摆架上,另一组安装在高精度位移台上,通过移动位移台调节两组梳齿电极的相对位置[29]。
静电梳既可以输出宽范围高精度稳态静电力,又能输出各种脉冲冲量,在推力架标定中得到了广泛应用。典型应用例如图14所示,杨超等[30]采用静电梳装置产生了0~900 μN的静电标定力,完成了对亚微牛级精度扭摆推力架的标定,该摆架已完成了对“太极一号”卫星搭载的微推进器的推力测试。在使用静电梳对推力架标定的过程中,摆臂摆动会导致梳齿啮合长度的变化,尽管理论上静电力与梳齿啮合长度无关,但由于加工误差等非理想因素的存在,仍会产生一定的误差。Selden等[31]的研究结果表明,对于梳齿啮合长度为5 mm的静电梳装置,当啮合长度改变1 mm时,静电力值变化约为2%。
相比于平行电极板装置,静电梳装置不存在边缘效应,精度较高,但其实际应用时受梳齿加工精度等因素限制,通常仍需要使用高精度天平对装置静电力输出进行校准。同时静电梳装置摆架位移距离受静电梳的梳齿啮合长度限制,此外装置还存在结构复杂、易损坏的缺点。
1.2.2 电磁力标定方法
电磁力标定方法是利用电流的磁效应产生标定力的方法。常用的电磁力产生装置有线圈—磁体结构和电磁铁—导线结构等。
(1)线圈—磁体装置
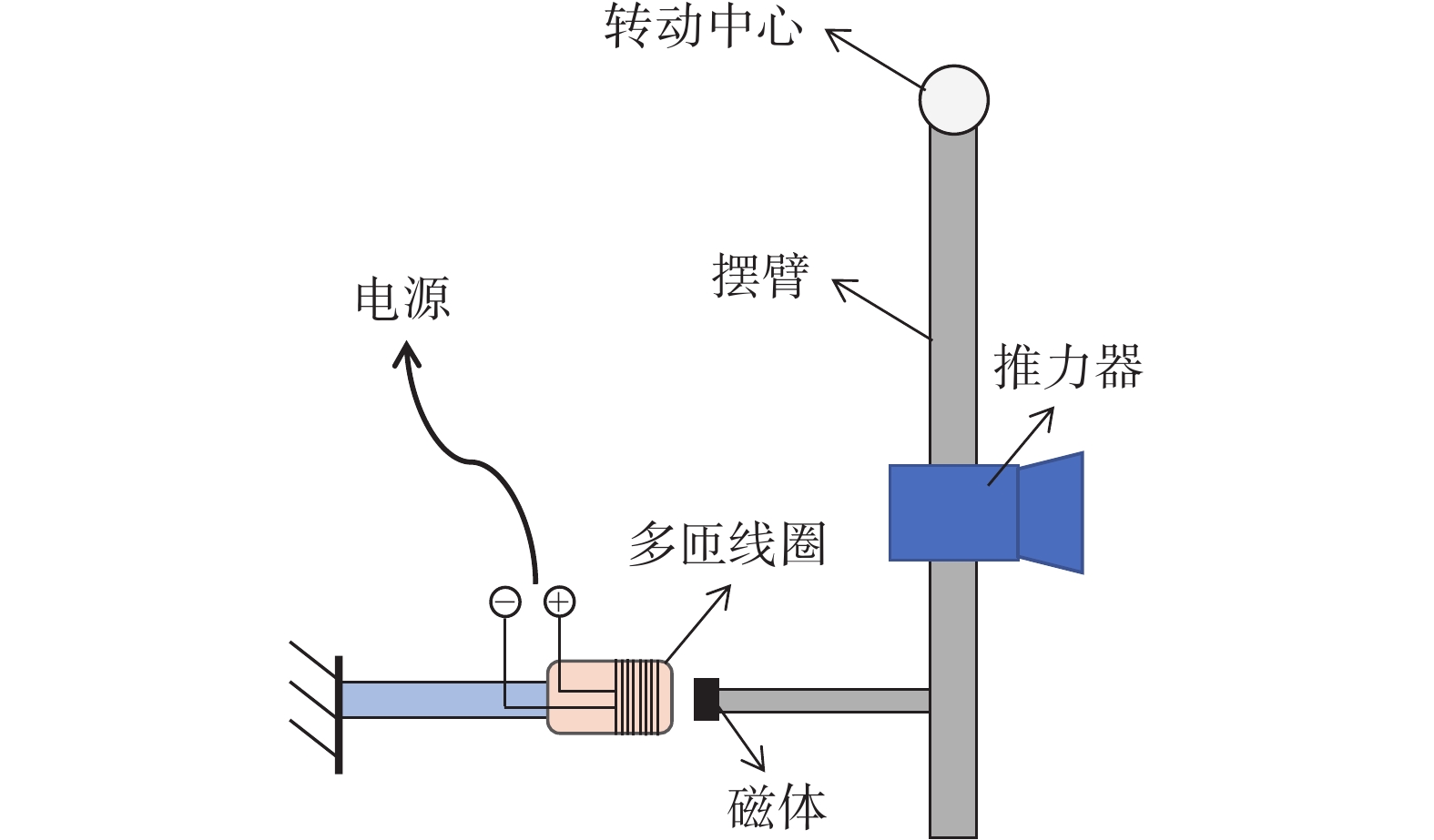
通电线圈在磁场中会受到安培力的作用。线圈—磁体装置使用基于该原理产生的力对摆架进行标定,如图15所示。
永磁体和垂直于磁力线的多匝线圈之间的作用力可由式(4)计算得出:
$$ {F}_{\mathrm{电}\mathrm{磁}}=2\mathrm{\pi }NBRI $$ (4) 式中:N为线圈匝数;B为磁感应强度;R为线圈半径;I为线圈电流。在使用线圈—磁体装置用于推力架标定时,为了尽可能地减小测控线圈对推力架的影响,通常将永磁体安装在推力架的转动部件上,将多匝线圈安装在固定部件上[32]。
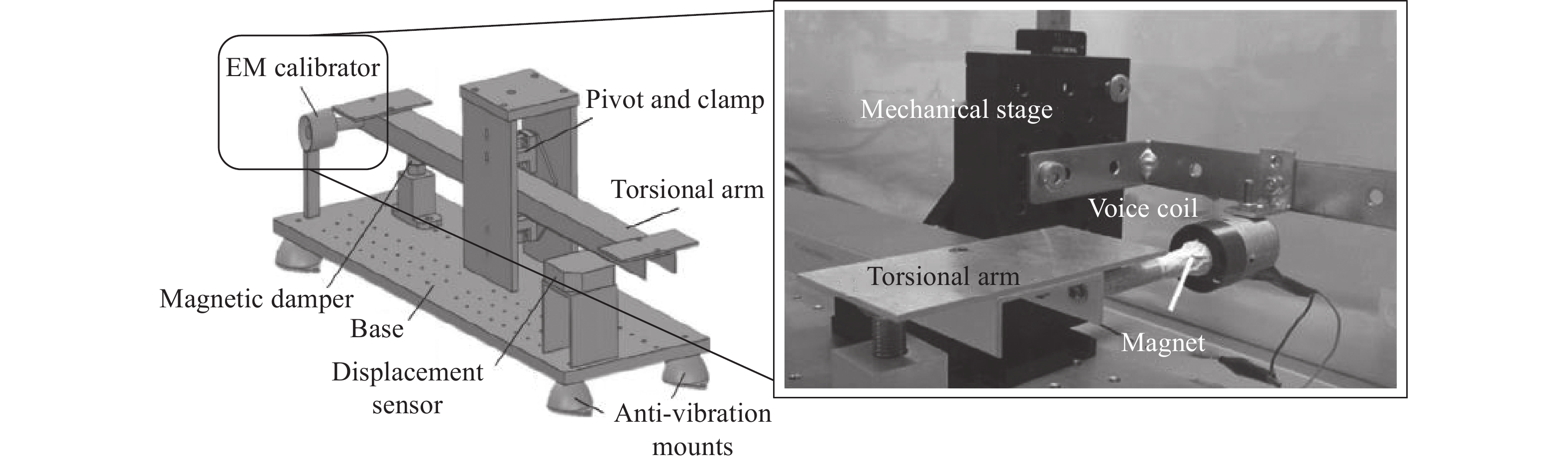
线圈—磁体装置原理简单易实现,通过调节电源电流可输出宽范围电磁力,在高精度推力架标定中得到了广泛应用。Lam等[33]利用音圈和永磁体构建了电磁力标定装置,应用于扭摆结构推力架的标定,如图16所示。该装置可产生30~23000 μN的宽范围稳态力值输出,呈现良好的线性和可重复性。同时该装置还能产生12~668 μN·s的冲量。装置稳态标定力和脉冲标定力的最大不确定度分别为18.48%和11.38%。Tang等[34]研发了一种使用永磁体和线圈的电磁校准技术,可产生10~1000 μN·s的微冲量和小于10 mN的电磁力。电磁校准力与线圈电流呈线性关系,当线圈与磁体距离变化6 mm时,校准力的变化小于2.5%。Zhou等[35]、Chang等[36]研究发现线圈与磁体相对位置会影响装置电磁力输出,对于测试使用的线圈—磁体装置,当线圈和磁体的轴向间距产生1 mm的变化时(设计轴向间距为1.5 mm),由于磁场的不均匀性,电磁力输出的误差约为3%。这说明在应用线圈—磁体装置产生稳态电磁力对摆架进行动态标定时,随着摆臂摆动力值输出将引入额外的误差。同时装置电磁力值输出易受到外界磁场环境干扰,误差难以准确评估。
(2) 电磁铁—导线装置
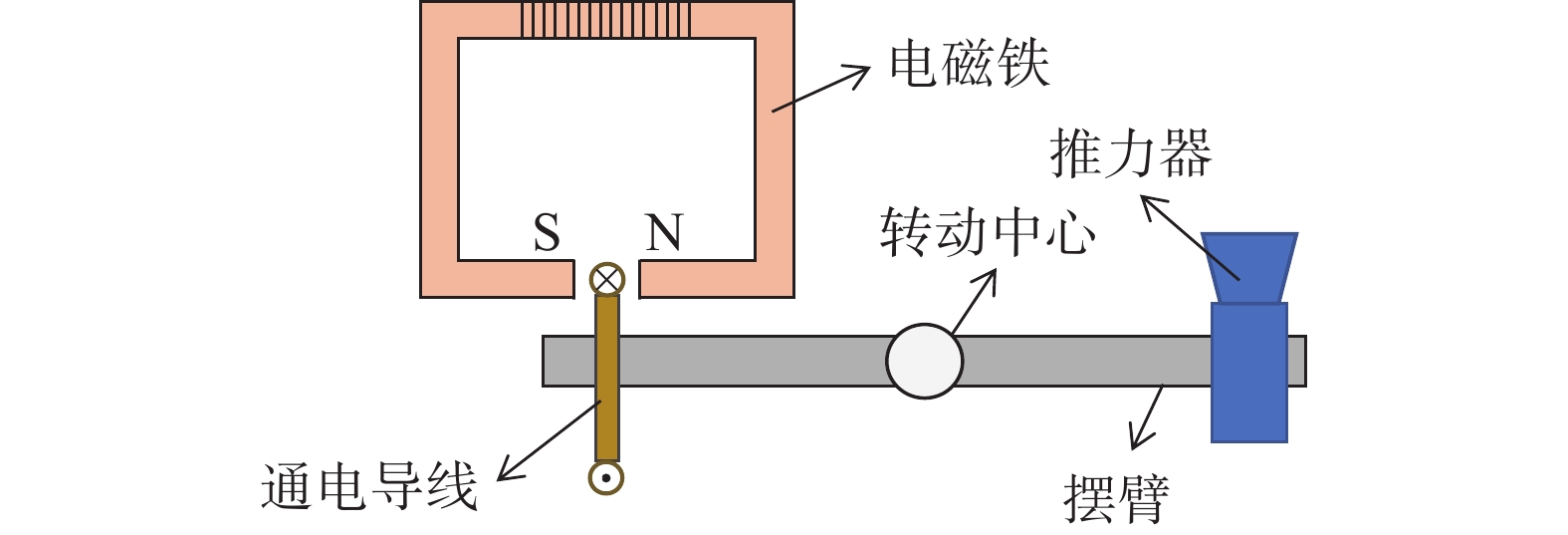
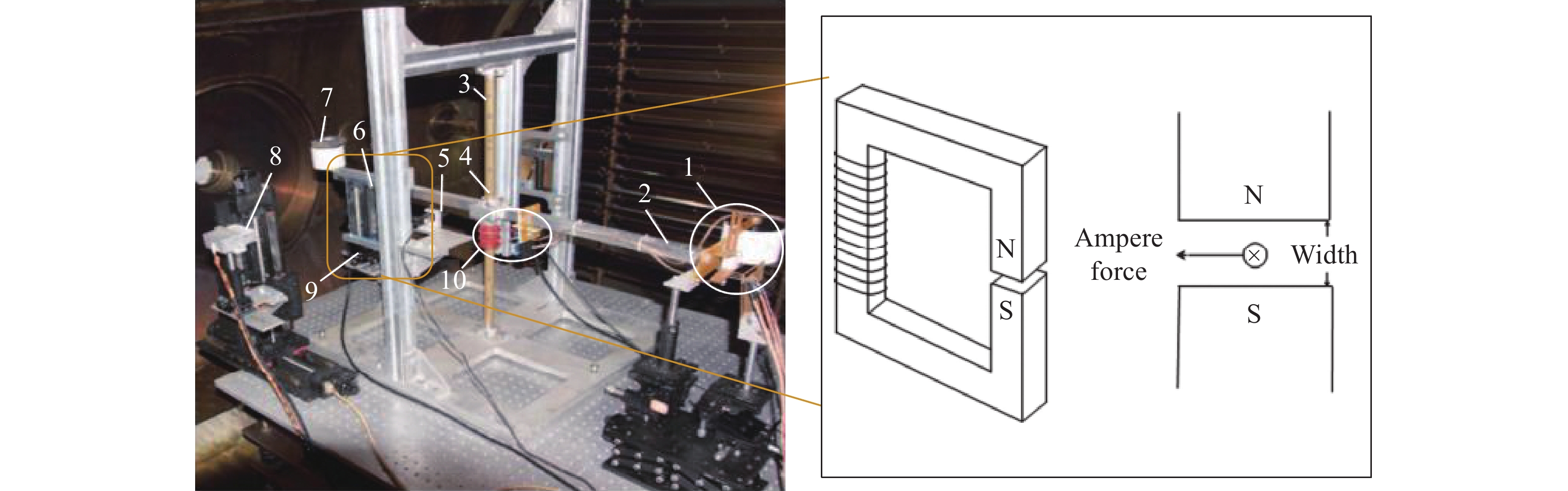
电磁铁—导线装置利用通电导线磁场中受到的安培力作为电磁力输出。其结构如图17所示,通过电磁铁在特定区域产生高密度磁场,将通以直流电的导线放置在磁场区域,导线在磁场中受到安培力的作用[37]:
$$ {F}_{电磁}=BIL $$ (5) 式中:L为磁场中的导线长度。
在使用电磁铁—导线装置进行推力架标定时,通常将通电导线安装在推力架的转动部件上,将电磁铁安装在固定部件上。典型应用例如图18所示[37-38],He等[37]、 Zhang等[38]在对微牛级悬丝扭摆结构推力架的标定中使用的电磁体导线装置,通过调节导线电流,可产生15.73~291.5 μN的电磁标定力。当标定力为150 μN时,误差为2.86%。
电磁体导线装置原理简单,可产生微牛级精度的标定力,且电磁力输出不受摆臂运动的影响,但由于磁极面边缘效应的存在,难以在导线区域形成均匀磁场,输出误差无法避免。此外,电磁铁铁芯的磁化会引入额外的不确定度。
1.2.3 气体动力学方法
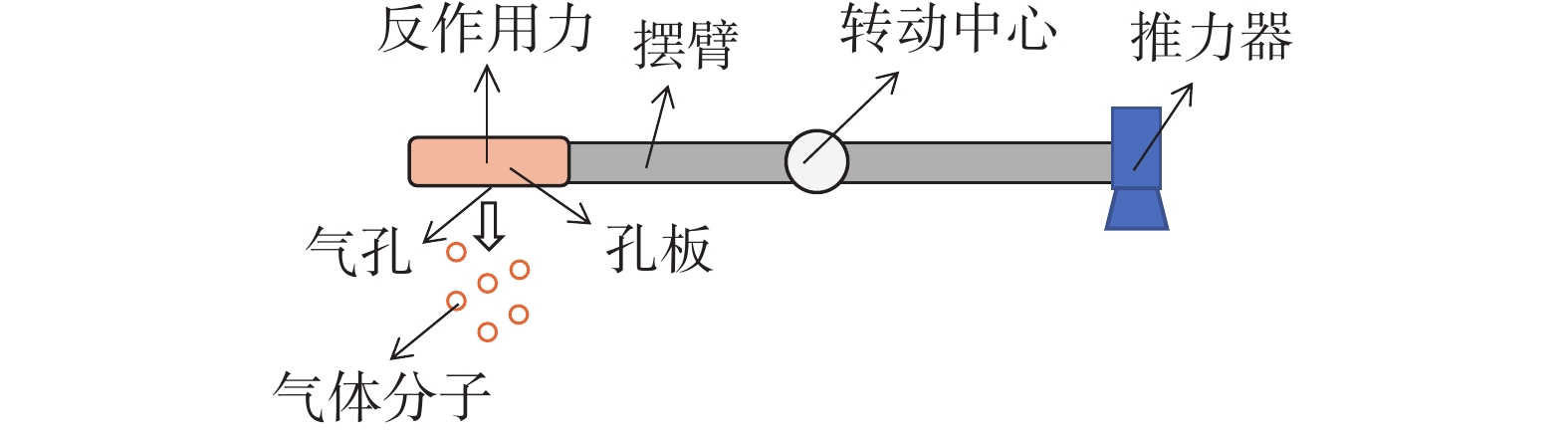
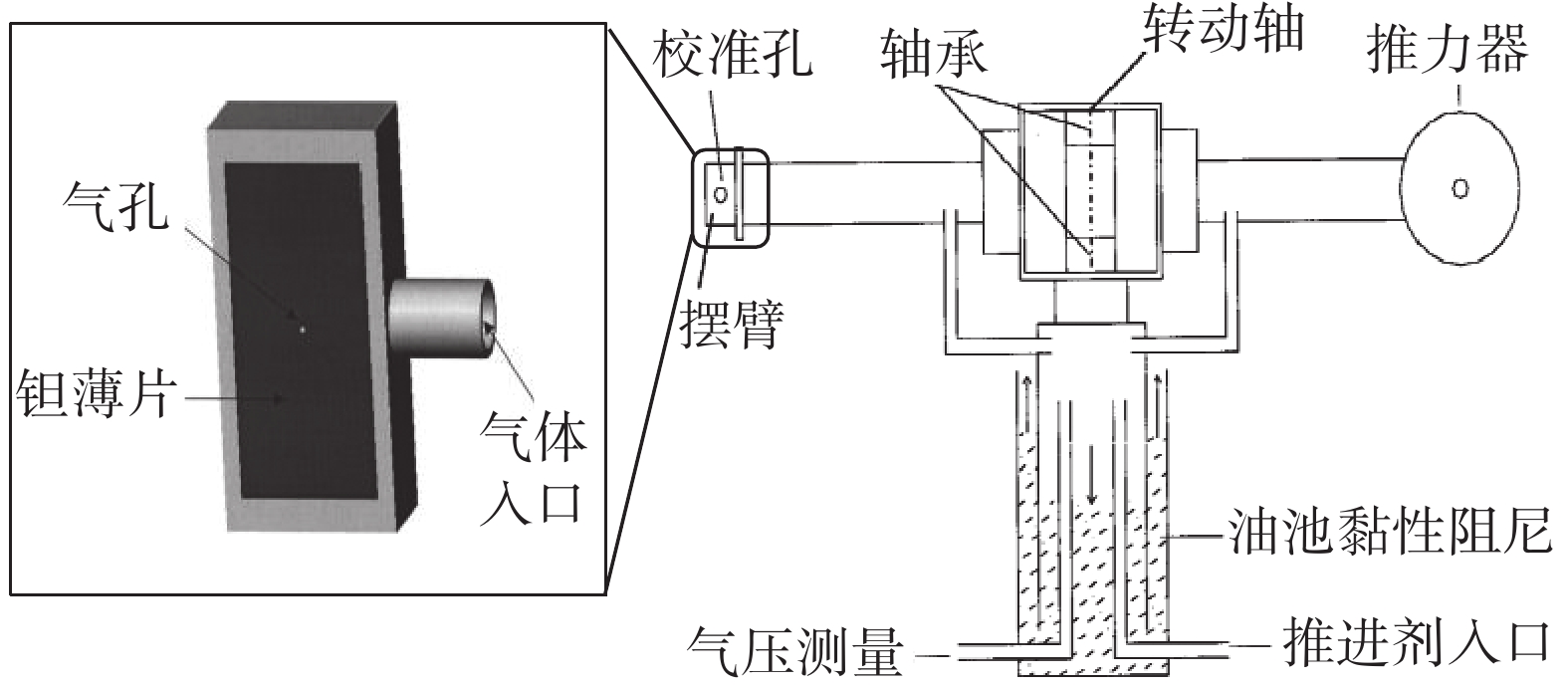
气体动力学方法利用气体的自由分子膨胀来产生力的作用,如图19所示。该方法通常应用于真空环境,此时气体分子平均自由程远大于其特征尺寸,满足自由分子膨胀假设,利用气体喷出产生的反作用力来产生标定力。典型应用实例为Jamison等[39]设计的薄壁孔板结构标定装置,如图20所示。对于满足薄壁假设($ \mathrm{t}/\mathrm{d} $≪1)的孔板,通过对大克努森数孔板流动实验和仿真计算,可获得孔口处力的解析解为[40]:
$$ {F}_{\mathrm{气}\mathrm{动}}=\frac{{p}_{0}}{2}\left(1-\frac{2{t}_{\mathrm{孔}\mathrm{板}}}{d}\right){A}_{\mathrm{孔}\mathrm{板}} $$ (6) 式中:$ {p}_{0} $为孔板滞止压力;$ {t}_{\mathrm{孔}\mathrm{板}} $为孔板厚度;$ d $为气孔直径;$ {A}_{\mathrm{孔}\mathrm{板}} $为孔板面积。通过对孔板结构的合理设计,可产生80 nN~1 μN范围的标定力,其中在86.2 nN处的误差为10.7%,在712 nN处的误差为2%。
除薄壁孔板装置外,也可使用其他喷气装置产生反作用力。Smith等[41]使用微流量气体推进器代替孔板装置产生标定力,力值范围1~10 μN。气体动力学方法可以产生纳牛级至微牛级范围的标定力,且装置易于实现,但这种方法仅能在真空环境应用,且属于间接标定方法,标定力无法进行力值溯源,力值输出的可信度难以保证。
2. 不同标定方法对比
不同标定方法特性及优缺点如表3所列。在接触式标定方法中基于重力作用的砝码滑轮结构原理简单,无须再校准,是mN~N范围最常用的标准力输出装置。但随着输出标准力降至μN级,尽管可寻找百μg级标准质量替代砝码[42],但滑轮摩擦和绳线弹性带来的误差无法避免,无法保证力值输出精度。力矩等效装置可以产生宽范围、高精度的标定力,但力矩等效过程会引入额外的不确定度和位置测量误差。
表 3 不同标定方法特性及优缺点Table 3. Characteristics,advantages and disadvantages of different calibration methods施加方式 原理 标定方法 力/冲量范围 误差来源 优/缺点 接触式 重力 绳系质量—滑轮装置 mN~N 滑轮摩擦和绳线弹性 易于实现,可溯源/力值间断,精度差 等效力矩装置 μN~N 等效关系偏差,位置测量精度 精度高、力值范围宽/等效关系偏差无法校准 冲击力 落球法 100~1000 μN·s 位置测量精度,碰撞阶跃响应 可溯源/适用范围窄,冲量间断 力锤法 10 ~10000 μN·s 力锤灵敏度 冲量范围宽,精度高/力锤控制要求高 冲击摆法 10 ~1000 μN·s 冲击摆参数测量精度 可溯源/装置复杂,响应慢 非接触式 静电力 静电平行板 μN~mN 力值非线性,边缘效应和板间距控制 输出力值精度高/极板位置控制要求高,应用受限 静电梳 μN~mN
1~10000 μN·s力值非线性 可提供高精度、宽范围力和冲量输出/装置结构复杂,应用受限 电磁力 线圈—磁体装置 μN~mN
1~1000 μN·s磁体不等价性,外界磁场影响 可提供高精度、宽范围力和冲量输出/易受电磁干扰,低力值输出不确定度高 电磁铁—导线装置 10~1000 μN
10~1000 μN·s磁场波动、电磁体磁化 易于实现,力值输出不受摆架运动影响/易受电磁干扰 气体分子反作用力 薄壁孔板装置 0.1~10 μN 孔口直径和滞止压力的测量误差,均匀扩散模型误差 可提供亚微牛级力值/力值无法溯源,可信度低 基于冲击力作用的几种标准力产生装置可提供μN·s~mN·s宽范围的冲量,但无法提供稳态作用力,因此常用于冲量测试推力架的校准。其中落球法冲量方向固定,适用的摆架种类较少;冲击摆法需要精确测量冲击摆的质量和速度,装置结构复杂,测量过程会引入额外的误差;力锤是应用较多的微冲量施加装置,可提供宽范围高精度微冲量,但力锤控制装置较为复杂,且为避免产生重复敲击,对位置控制精度和驱动器响应时间的要求较高。
在非接触式标定方法中,基于静电力作用的静电平行板装置结构简单易操作,精度较高,但输出力值对平板间距敏感。然而在校准摆架的过程中,摆架受力作用后位置会发生变化,平板间距难以控制和精确测量,输出精度难以保证。平行板电容器通过测量电容梯度的方法,规避了输出力值对间距敏感的问题,但电容梯度测量系统较为复杂。静电梳通过特殊的构型,在一定范围内降低了输出力值对间距的敏感性,同时规避了边缘效应,输出精度高,在高精度推力架标定中具有广泛应用。
基于电磁力作用的两种装置结构简单易实现,均可输出宽范围的力和冲量,理论上均可以获得较高的精度。但在实际操作中,当采用线圈—磁体装置时,多匝线圈与永磁体的相对位置需要精确控制。当间隙过小时,保持磁铁和线圈之间的精确对准较难;间隙过大时,边缘效应增大,直接影响到作用力的特性。当采用电磁铁—导线装置时,磁极面边缘化产生的漏磁和电磁铁的磁化难以避免[43]。此外,受磁体不等价性、边缘效应及外界磁场干扰等因素的影响,磁场不均匀性带来的误差难以估计,电磁力输出的精度无法保证。
基于自由分子膨胀作用的气体动力学方法易于实现和应用,可获得nN级至μN级的力值输出精度。但该方法属于间接标定方法,标定力无法进行力值溯源,力值输出的可信度难以保证。
通过对比可以看出,不同标定技术的特点及适用范围有很大差异。当需要的标定力在mN以上数量级时,接触式标定方法尤其是基于重力作用的绳系质量—滑轮装置,具有原理清晰可溯源、易于实现的特点,在推力架标定中应用广泛。随着标定力降低至μN级,接触作用带来的误差难以避免,基于静电力和电磁力原理的非接触式标定技术得到了广泛应用。当标定力为nN级时,由于边缘效应、电磁干扰等因素影响,静电力和电磁力产生装置的精度难以保证。目前尚缺少高精度、可溯源的nN级标定力产生和施加技术,需要对现有方法进行改进优化或提出新的标定技术,以满足如天基引力波探测等高精度空间科学任务的微推进器测力机构标定需求。
3. 总结
调研了推力架的标定技术和方法,应用场景以及各自的特点。如针对测量精度为mN级的推力架,重力法是常用的稳态标准力产生技术;基于冲击力作用的力锤和冲击摆装置,可以提供宽范围冲量,常用于脉冲推力测试推力架标定;基于静电力和电磁力的标定技术具有精度高、响应快、可以同时提供宽范围稳态力和冲量的优点,已广泛应用于mN级、μN级精度推力架的标定过程,但其受边缘效应、电磁干扰等非理想因素影响,需要对装置电信号与力值输出关系进行再校准;气体动力学标定方法可产生亚微牛级的标定力,但该方法属于间接标定方法,无法进行力值溯源。
随着航天技术的发展,复杂化、多样化的空间任务对推进器推力范围、分辨率和稳定性等参数指标的要求不断提高,对推力架测量能力提出了更高要求。针对该趋势,未来对推力架的标定,一方面可综合各类标定技术特点,采用多种标定方法相结合的标定方案,降低或抵消标定装置或标定操作对推力架标定结果产生的影响;另一方面,通过提出原理清晰、置信度高、操作简单、可溯源的亚微牛级标准力产生和施加技术,满足更高精度推力架的标定需求。
-
表 1 高精度空间任务推进系统参数
Table 1 Parameter of high-precision space mission propulsion system
表 2 典型推力架结构特点及应用
Table 2 Structural characteristics and applications of typical thrust stand
推力架类型 特点 研究机构 性能参数 应用 悬摆结构 回复力为重力,稳定,无温漂;非线性,灵敏度和极限承载质量难以兼得。 The French Aerospace Lab[14] 测量范围:0.1~1000 μN
分辨率<0.1 μNGAIA任务冷气和FEEP
推力测试倒摆结构 结构紧凑,灵敏度高,承重大;结构不稳定,需要主动控制,易受温度影响。 MIT Space Propulsion Lab[15] 测量范围:0~23 mN
不确定度:±0.5 mN用于卫星轨道控制Hall
推力器推力测试扭摆结构 测量范围宽,测量精度不受重力影响,回复力线性;尺寸较大,需要配平,易受温度影响。 NASA Goddard Space Flight Center[16] 测量范围:1~100 μN
分辨率0.1 μNLISA任务胶体和FEEP
推力测试天平结构 易于校准,可以测量推进剂质量损失;需要配平,不适用于小推重比测量。 东京大学[17] 推力测量范围:0~1600 μN
冲量测量范围:0~1000 μN·s
误差<5%ALOS-3卫星PPT
推力测试表 3 不同标定方法特性及优缺点
Table 3 Characteristics,advantages and disadvantages of different calibration methods
施加方式 原理 标定方法 力/冲量范围 误差来源 优/缺点 接触式 重力 绳系质量—滑轮装置 mN~N 滑轮摩擦和绳线弹性 易于实现,可溯源/力值间断,精度差 等效力矩装置 μN~N 等效关系偏差,位置测量精度 精度高、力值范围宽/等效关系偏差无法校准 冲击力 落球法 100~1000 μN·s 位置测量精度,碰撞阶跃响应 可溯源/适用范围窄,冲量间断 力锤法 10 ~10000 μN·s 力锤灵敏度 冲量范围宽,精度高/力锤控制要求高 冲击摆法 10 ~1000 μN·s 冲击摆参数测量精度 可溯源/装置复杂,响应慢 非接触式 静电力 静电平行板 μN~mN 力值非线性,边缘效应和板间距控制 输出力值精度高/极板位置控制要求高,应用受限 静电梳 μN~mN
1~10000 μN·s力值非线性 可提供高精度、宽范围力和冲量输出/装置结构复杂,应用受限 电磁力 线圈—磁体装置 μN~mN
1~1000 μN·s磁体不等价性,外界磁场影响 可提供高精度、宽范围力和冲量输出/易受电磁干扰,低力值输出不确定度高 电磁铁—导线装置 10~1000 μN
10~1000 μN·s磁场波动、电磁体磁化 易于实现,力值输出不受摆架运动影响/易受电磁干扰 气体分子反作用力 薄壁孔板装置 0.1~10 μN 孔口直径和滞止压力的测量误差,均匀扩散模型误差 可提供亚微牛级力值/力值无法溯源,可信度低 -
[1] FLECHTNER F,SNEEUW N,SCHUH W D. Observation of the system earth from space:CHAMP,GRACE,GOCE and future missions[M]. Publisher Name: Springer,Berlin, Heidelberg,2014.
[2] 罗子人,白姗,边星,等. 空间激光干涉引力波探测[J]. 力学进展,2013,43(4):415−447. doi: 10.6052/1000-0992-13-044 [3] DEBRA D B. Drag-free control for fundamental physics missions[J]. Advances in Space Research,2003,32(7):1221−1226. doi: 10.1016/S0273-1177(03)90321-8
[4] FUNAKI I,NAKAYAMA Y,HORISAWA H,et al. Micro-thruster options for the Japanese space gravitational wave observatory missions[C]//IEPC,Presented at the 32nd International Electric Propulsion Conference,2011.
[5] LIENART T. Design,manufacturing and testing of the cold gas propulsion system for CNES' microscope spacecraft:lessons learnt[C]//53rd AIAA/SAE/ASEE Joint Propulsion Conference,2017.
[6] CANUTO E,MASSOTTI L. All-propulsion design of the drag-free and attitude control of the European satellite GOCE[J]. Acta astronautica,2009,64(2-3):325−344. doi: 10.1016/j.actaastro.2008.07.017
[7] ZIEMER J,RANDOLPH T,FRANKLIN G,et al. Delivery of colloid micro-Newton thrusters for the space technology 7 mission[C]//44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit,2008.
[8] ARMANO M,AUDLEY H,BAIRD J,et al. LISA Pathfinder micronewton cold gas thrusters:In-flight characterization[J]. Physical review D,2019,99(12):122003. doi: 10.1103/PhysRevD.99.122003
[9] LUO J,CHEN L S,DUAN H Z,et al. TianQin:a space-borne gravitational wave detector[J]. Classical and Quantum Gravity,2016,33(3):035010. doi: 10.1088/0264-9381/33/3/035010
[10] LUO Z,GUO Z K,JIN G,et al. A brief analysis to Taiji:Science and technology[J]. Results in Physics,2020,16:102918. doi: 10.1016/j.rinp.2019.102918
[11] ZHOU W,YE J,LI N,et al. Configurations and key issues of low thrust measurement for microspacecrafts[C]//MATEC Web of Conferences. EDP Sciences,2018,179:03010.
[12] ZHANG H,DUAN B,WU L,et al. Development of a steady-state microthrust measurement stand for microspacecrafts[J]. Measurement,2021,178:109357. doi: 10.1016/j.measurement.2021.109357
[13] 洪延姬,周伟静,王广宇. 微推力测量方法及其关键问题分析[J]. 航空学报,2013,34(10):2287−2299. [14] JARRIGE J,THOBOIS P,BLANCHARD C,et al. Thrust measurements of the Gaia mission flight-model cold gas thrusters[J]. Journal of Propulsion and Power,2014,30(4):934−943. doi: 10.2514/1.B35091
[15] TARTLER B R. Construction and performance of an inverted pendulum thrust balance[D]. Massachusetts Institute of Technology,2010.
[16] MERKOWITZ S M,MAGHAMI P G,SHARMA A,et al. A μNewton thrust-stand for LISA[J]. Classical and Quantum Gravity,2002,19(7):1745-1750. doi: 10.1088/0264-9381/19/7/370
[17] YOSHIKAWA T,TSUKIZAKI R,KUNINAKA H. Calibration methods for the simultaneous measurement of the impulse,mass loss,and average thrust of a pulsed plasma thruster[J]. Review of Scientific Instruments,2018,89(9):095103. doi: 10.1063/1.5027047
[18] POLK J E,PANCOTTI A,HAAG T,et al. Recommended practice for thrust measurement in electric propulsion testing[J]. Journal of Propulsion and Power,2017,33(3):539−555. doi: 10.2514/1.B35564
[19] MOELLER T,POLZIN K A. Thrust stand for vertically oriented electric propulsion performance evaluation[J]. Review of Scientific Instruments,2010,81(11):115108. doi: 10.1063/1.3502463
[20] POLZIN K A,MARKUSIC T E,STANOJEV B J,et al. Thrust stand for electric propulsion performance evaluation[J]. Review of Scientific Instruments,2006,77(10):105108. doi: 10.1063/1.2357315
[21] TREZZOLANI F,MAGAROTTO M,MANENTE M,et al. Development of a counterbalanced pendulum thrust stand for electric propulsion[J]. Measurement,2018,122:494−501. doi: 10.1016/j.measurement.2018.02.011
[22] ZIEMER J K. Performance measurements using a sub-micronewton resolution thrust stand[C]//27th International Electric Propulsion Conference,2001.
[23] PANCOTTI A P,GILPIN M,HILARIO M S. Comparison of electrostatic fins with piezoelectric impact hammer techniques to extend impulse calibration range of a torsional thrust stand[J]. Review of Scientific Instruments,2012,83(3):035109. doi: 10.1063/1.3690385
[24] HAAG T W. Thrust stand for pulsed plasma thrusters[J]. Review of Scientific Instruments,1997,68(5):2060−2067. doi: 10.1063/1.1148097
[25] SONI J,ROY S. Design and characterization of a nano-Newton resolution thrust stand[J]. Review of Scientific Instruments,2013,84(9):095103. doi: 10.1063/1.4819252
[26] GAMERO-CASTANO M. A torsional balance for the characterization of microNewton thrusters[J]. Review of scientific instruments,2003,74(10):4509−4514. doi: 10.1063/1.1611614
[27] WANG B,YANG Y,HU Z,et al. The Traceable calibration of thrust stand by electrostatic force[J]. Journal of Visualized Experiments,2022(181):63465.
[28] CHEN C,LEE C. Design and modeling for comb drive actuator with enlarged static displacement[J]. Sensors and Actuators A:Physical,2004,115(2/3):530−539. doi: 10.1016/j.sna.2004.04.052
[29] WANG Y,DING W,CHENG L,et al. Development and analysis of a novel printed circuit board electrostatic comb system for micro-newton thrust stand calibration[J]. Review of Scientific Instruments,2018,89(7):075104. doi: 10.1063/1.5019401
[30] 杨超,贺建武,康琦,等. 亚微牛级推力测量系统设计及实验研究[J]. 中国光学,2019,26(8):1945−1953. [31] SELDEN N P,KETSDEVER A D. Comparison of force balance calibration techniques for the nano-Newton range[J]. Review of Scientific Instruments,2003,74(12):5249−5254. doi: 10.1063/1.1623628
[32] WONG A R,TOFTUL A,POLZIN K A,et al. Non-contact thrust stand calibration method for repetitively pulsed electric thrusters[J]. Review of Scientific Instruments,2012,83(2):025103. doi: 10.1063/1.3680557
[33] LAM J K,KOAY S C,CHEAH K H. Electromagnetic calibration system for sub-micronewton torsional thrust stand[J]. IOP Conference Series:Materials Science and Engineering,2017,270(1):012011.
[34] TANG H B,SHI C,ZHANG X,et al. Pulsed thrust measurements using electromagnetic calibration techniques[J]. Review of Scientific Instruments,2011,82(3):035118. doi: 10.1063/1.3567803
[35] ZHOU W J,HONG Y J,CHANG H. A microNewton thrust stand for average thrust measurement of pulsed microthruster[J]. Review of Scientific Instruments,2013,84(12):125115. doi: 10.1063/1.4850637
[36] CHANG H,ZHOU W,HONG Y,et al. Output force characterization of the electromagnetic calibration device for low thrust measurement[J]. IEEE Transactions on Instrumentation and Measurement,2021,70:1−9.
[37] HE Z,WU J,ZHANG D,et al. Precision electromagnetic calibration technique for micro-Newton thrust stands[J]. Review of Scientific Instruments,2013,84(5):055107. doi: 10.1063/1.4804285
[38] ZHANG D,WU J,ZHANG R,et al. High precision micro-impulse measurements for micro-thrusters based on torsional pendulum and sympathetic resonance techniques[J]. Review of Scientific Instruments,2013,84(12):125113. doi: 10.1063/1.4850615
[39] JAMISON A J,KETSDEVER A D,MUNTZ E P. Gas dynamic calibration of a nano-Newton thrust stand[J]. Review of Scientific Instruments,2002,73(10):3629−3637. doi: 10.1063/1.1505096
[40] ALEXEENKO A A,GIMELSHEIN S F,LEVIN D A,et al. Measurements and simulation of orifice flow for micropropulsion testing[J]. Journal of propulsion and power,2003,19(4):588−594. doi: 10.2514/2.6170
[41] SMITH B J,BLACK J T,ADAMS C S. Design and calibration of a torsion pendulum for micronewton-class spacecraft thrusters[J]. Journal of Aerospace Engineering,2022,35(3):4022023. doi: 10.1061/(ASCE)AS.1943-5525.0001408
[42] HU M H,WANG J,ZHANG Y,et al. Research on micro-gram weight standards below 1 mg in NIM[C]//Proc XX IMEKO World Congress,Metrology for Green Growth (Busan,Republic of Korea,9–14 September 2012),2012.
[43] LAM J K,KOAY S C,LIM C H,et al. A voice coil based electromagnetic system for calibration of a sub-micronewton torsional thrust stand[J]. Measurement,2019,131:597−604. doi: 10.1016/j.measurement.2018.09.029
-
期刊类型引用(1)
1. 何雨璐,封锋,王泽文,沈小东,郭洪靖. 基于均匀磁场标定的微动力测试平台研究. 固体火箭技术. 2024(05): 730-737 .  百度学术
百度学术
其他类型引用(0)




 下载:
下载: